Урок алгебри в 8 класі. "Крізь терни до зірок. Неповні квадратні рівняння"

Клас: 8

 

Тема: Крізь терни до зірок. Означення квадратного рівняння. Неповні квадратні рівняння, їх розв’язування.

 

Мета:

• сформувати в учнів поняття квадратного рівняння, неповного квадратного рівняння;
• формувати вміння розв’язувати неповні квадратні рівняння, а також навички виконувати дії відповідно до алгоритму розв’язування неповних квадратних рівнянь;
• розвивати вміння відтворювати зміст вивченого на уроці матеріалу;
• розвивати логічне  мислення, просторове уявлення, формувати математичну мову, вміння аналізувати, порівнювати й робити висновки;
• сприяти формуванню активної життєвої позиції, вміння висловлювати свої думки, виховувати культуру спілкування.

 

Обладнання: зірки з завданнями, зірки для схеми «Коефіцієнти квадратного рівняння», картки для складання схеми «Квадратні рівняння», картки з розв’язками самостійної роботи.

 

Тип уроку: засвоєння нових знань і умінь.

 

Форма проведення: уявна подорож

 

Хід уроку:

 

І. Організаційний етап.

 

Діти записують зошитах число, вид роботи.

 

- Відомий науковець і дослідник Ейнштейн говорив: «Мені доводиться розподіляти свій час між політикою і рівняннями. Але рівняння, на мою думку важливіші». Саме тому він був найкращим в розв’язуванні рівнянь, він досяг у цьому  найбільших висот. Але ви знаєте, що в житті, щоб чогось досягти, необхідно докласти зусилля і пройти через багато труднощів, пройти через терни. І тільки той, хто не зупинився, подолав ці перешкоди зможе «дістати зірку з неба» і отримати винагороду у вигляді задоволення від гарно зробленої роботи. Тому сьогодні ми з вами вирушаємо в нову подорож «Крізь терни до зірок».

 

ІІ. Актуалізація опорних знань.

 

Фронтальне опитування

 

• Що називається рівнянням? (Рівняння – це рівність, що містить змінну)
• Наведіть приклади рівнянь.
• Що означає розв’язати рівняння? (Розв’язати рівняння – це означає знайти його розв’язки або довести, що їх немає)
• Що називають розв’язком або коренем рівняння? (Це значення змінної, при якому рівняння перетворюється у правильну рівність)
• Які рівняння називаються рівносильними? (Рівняння, які мають однакові розв’язки або не мають їх)
• Які рівняння називають лінійними рівняннями з однією змінною? (Рівняння виду ах+в=с)
• Наведіть приклади таких рівнянь.
• Скільки розв’язків може мати лінійне рівняння з однією змінною? (один або жодного)

 

ІІІ. Мотивація навчальної діяльності.

 

«Мозковий штурм»

 

• Розв’яжіть задачу, склавши рівняння з однією змінною: Знайти числа, одне з яких більше від другого на 3, а їхній добуток дорівнює 270.

 

Короткий запис:

 

І ч.  – х

ІІ ч. – х + 3

 

Рівняння: х (х + 3) = 210

 

• Чи можете ви розв’язати дане рівняння? Чому?

 

 

IV. Повідомлення теми, мети, завдань уроку.

 

• Сьогодні наш шлях веде до зірки, яка називається Квадратні рівняння. Наше завдання сформувати поняття квадратного рівняння та неповного квадратного рівняння. Познайомитися з видами неповних квадратних рівнянь і навчитися їх розв’язувати.
• Запишіть тему в зошити: Квадратні рівняння. Неповні квадратні рівняння.
• А тепер вперед до зірок!

 

V. Вивчення нового матеріалу.

 

1. Означення квадратного рівняння. Коефіцієнти квадратного рівняння.

 

1. Виведення формули квадратного рівняння. (сильний учень на дошці)

 

• Давайте спростимо наше рівняння:

х (х + 3) = 210

х² + 3х = 210

х² + 3х -  210 = 0

• Замінимо числа на літери а, b, с:

ах² + bх -  с  = 0

(дістаємо першу зірочку з написом: ах² + bх +  с  = 0 і вішаємо на дошці)

• Це рівняння другого степеня з однією змінною або квадратне рівняння.

 

2. Вивчення означення квадратного рівняння. (робота з підручником)

 

• Відкрийте підручники на сторінці 185. Знайдіть означення квадратного рівняння. Перепишіть його в зошити.
• Яке рівняння називається квадратним? (Квадратним називається рівняння виду ах² + bх +  с  = 0, де х – змінна; а, b, с – деякі числа, причому а)
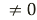
• Чому, на вашу думку ставиться умова, щоб а?(Бо тоді рівняння стане простим лінійним рівнянням з однією змінною)
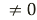
• Чим є а, b, с? (Числа)

 

3. Складання схеми «Коефіцієнти квадратного рівняння» (вчитель на дошці)

 

• У квадратному рівнянні ці числа називаються коефіцієнтами:

а – І коефіцієнт;

b – ІІ коефіцієнт;

с – ІІІ коефіцієнт

(ще три зірочки приєднуються до першої у вигляді схеми)

 

4. Первинне часткове засвоєння нового матеріалу. (Робота парами)

 

• Кожен з вас отримав зірочку на якій написано рівняння. Ваше завдання разом з сусідом вибрати тільки квадратні рівняння і підкреслити в них І коефіцієнт однією лінією, ІІ коефіцієнт – двома, вільний член – хвилястою лінією.

 

 

 

 

 

 

 

 

 

 

 

 

 

(Правильність виконання перевіряється  на дошці – один учень пояснює виконання)

 

2. Неповні квадратні рівняння.

 

1. Робота з опорною схемою «Квадратні рівняння» (колективна робота)

• На дошці ви бачите схему «Квадратні рівняння», але вона незакінчена. Як бачите всі квадратні рівняння діляться на повні і неповні. Якщо в квадратному рівнянні будуть присутні всі коефіцієнти, то рівняння буде повним.

 

• Ми вже знаємо, що І коефіцієнт не може дорівнювати нулю. А що буде, якщо ІІ коефіцієнт або вільний член, або ж обоє разом будуть рівними нулю? Давайте дізнаємося.

• якщо b=0, то рівняння набуде вигляду: ах² +  с  = 0;
• якщо с = 0, то рівняння набуде вигляду: ах² + bх  = 0;
• якщо b=0, с = 0, то рівняння набуде вигляду: ах² = 0.

 

2. Первинне часткове засвоєння нового матеріалу. (Робота з підручником, діти усно ланцюжком виконують №867)

 

3. Способи розв’язання неповних квадратних рівнянь.

 

     1) Робота в групах з підручником.

 

• А як розв’язати неповні квадратні рівняння? У нас є три види неповних квадратних рівнянь і три ряди парт. Учні на кожному ряду об’єднуються в групи і отримують завдання - розв’язати рівняння:

• І група - №872 (а)
• ІІ група - №870 (а)
• ІІІ група - №871 (а)

• Розв’язки діти записують на зірочках. Потім один учень з групи на дошці пояснює розв’язування рівняння.

 

2. Робота з опорною схемою «Квадратні рівняння»

 

(Записую формули для знаходження коренів рівняння на опорній схемі на дошці, учні – в зошитах)

 

4. Кількість коренів неповного квадратного рівняння.

 

Питання з зірочки: Скільки коренів може бути у квадратного рівняння? (жодного, один, два)

 

 

 

 

VІ. Закріплення нових знань і умінь.

 

1. Самостійна робота.

 

Завдання з зірочки: Розв’язати рівняння №874 за варіантами (І варіант – перший стовпчик, ІІ варіант – другий стовпчик).

 

(Перевірка здійснюється за зразком, які діти отримують додому)

№674 (І варіант)

 

1. 

 

в) 4

 

№674 (IІ варіант)

 

 

г) 8

=0

 

 

 

VІІ. Домашнє завдання.

 

1. Опрацювати текст підручника §19.
2. Виконати письмово №869, №873 (розв’язати неповні квадратні рівняння)
3. Творче завдання: Скласти 5 рівнянь, які б зводились до неповних квадратних рівнянь і розв’язати їх.

 

VІІІ. Підсумок уроку.

 

Рефлексія.

 

• Що вам запам’яталося  на сьогоднішньому уроці?
• Що було найлегше виконувати?
• Коли у вас виникали труднощі?