Урок алгебри в 9 класі "Розв'язування систем рівнянь з двома змінними із застосуванням різних способів"
Тема. Розв’язування систем рівнянь з двома змінними із застосуванням різних способів
Клас: 9
Мета:
навчальна: узагальнити і систематизувати способи розв’язування систем рівнянь, формувати вміння і навички досліджувати і розв’язувати системи рівнянь другого степеня з двома змінними;
розвивальна: розвивати пізнавальну компетентність, логічне мислення, увагу, пам'ять, спонукати
виховна: виховувати в учнях впевненість учнів до творчої активності, ініціативи, прагнення досягати високих результатів ; в своїх силах, акуратність, охайність, уважність, прагнення до самовдосконалення та саморозвитку.
Тип уроку: узагальнення та систематизація знань, умінь і навичок.
Методи і прийоми: репродуктивна діяльність, частково-пошуковий метод, робота в парах «Мозковий центр», побудова графіків функцій, демонстрація, вправи: «Мій настрій», «Мій діагноз», метод «Мікрофон», метод «Прес»
Засоби навчання: підручник «Алгебра: підручник для 9 класу», комп’ютерна презентація, картки із завданнями, кольорові листочки, магнітна дошка.
Оформлення дошки:
По центру: запис теми уроку
Зліва: епіграф: «Розум полягає не тільки у знанні, але й у вмінні застосовувати знання на ділі» ( Арістотель)
По центру: девіз уроку: «Успіх приходе до того, хто його прагне»
Справа: екран.
Перебіг уроку
І. Мотиваційний етап
1. Створення емоційного настрою, налаштування учнів на робочий лад. Вправа «Мій настрій»
Перед вами кольорові листочки. Пропоную вам обрати колір, який відповідає вашому настрою на цю мить. Якщо ваш настрій піднесений, гарний, то обираєте червоний листочок, якщо настрій нейтральний, то – зелений, якщо поганий, то – синій.
Не дивлячи на настрій з яким ви прийшли сьогодні на урок я вам усім бажаю гарного настрою, а тим у кого він зараз такий, прикладемо всіх зусиль, щоб його поліпшити. І пам’ятайте, що «Успіх приходить до того, хто його прагне». Нехай ці слова стануть сьогодні вашим девізом!
2. Актуалізація опорних знань і суб’єктивного досвіду
1. Усне опитування (метод «Мікрофон»):
1) Що є розв’язком системи рівнянь з двома змінними? (Розв’язком системи рівнянь з двома змінними є пара значень змінних, що перетворюють кожне рівняння системи у правильну числову рівність)
2) Які методи розв’язування систем рівнянь з двома змінними ви знаєте? (Системи рівнянь можна розв’язати такими методами: графічним; підстановки, додавання, заміна змінних)
3) Які недоліки графічного методу розв’язування систем рівнянь? (графічний спосіб не гарантує того, що отриманий результат є точним)
4) Коли графічний метод розв’язування рівнянь є ефективним? (коли потрібно визначити кількість розв’язків системи або достатньо знайти їх наближено)
5) У чому полягає сутність методу підстановки? (в заміні даної системи рівнянь рівносильною системою, в якій одне з рівнянь містить тільки одну змінну)
6) Які системи рівнянь можна розв’язати методом додавання? (систему рівнянь, в якій коефіцієнти при одній і тій самій змінній в обох рівняннях є протилежними числами)
2. Усне виконання вправ (Метод «Прес»).
1. Яка пара чисел буде розв’язком системи рівнянь? Один учень дає правильну відповідь і обґрунтовує її теоретично ![]()
А)(-1;4); Б)(1; -4); В)(2; 1); Г) (4; 1); Д) (-2; -2)
2. Визначити, який метод раціонально застосувати під час розв'язування даних систем рівнянь.
1) 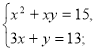 2)
2)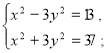 3)
3) 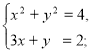 4)
4) 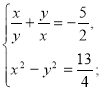
5) ![]() 6)
6) 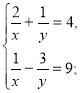 7)
7) 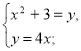 8)
8) 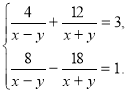
Відповіді:
1) метод підстановки,
2) метод додавання,
3) графічний метод,
4) метод заміни змінних,
5) метод підстановки,
6) метод додавання,
7) графічний метод,
8) метод заміни змінних.
Згадати алгоритми розв’язування систем рівнянь різними методами.
ІІ. Етап цілевизначення і планування діяльності
- Ознайомлення учнів з темою і метою уроку
Предметом дослідження на уроці буде тема «Розв’язування систем рівнянь з двома змінними із застосуванням різних способів».
Це питання надзвичайно важливе, воно протягом трьох років розглядається в шкільному курсі математики. Чому так багато часу відводиться для вивчення цієї теми? Та тому, що багато задач економіки, фізики зводяться до розв’язування систем рівнянь. Який із методів є кращим, раціональнішим? Якому методу надати перевагу? Спробуємо розібратися на уроці.
- Робота з епіграфом
Епіграфом сьогоднішнього уроку є слова Арістотеля «Розум полягає не тільки у знанні, але й у вмінні застосовувати знання на ділі»
ІІІ. Етап опрацювання навчального матеріалу
- Робота в парах «Мозковий центр». (Учні працюють в парах над розв’язуванням систем рівнянь, розв’язки презентують на дошці пояснюючи алгоритм розв’язування)
Перша пара – метод додавання
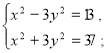
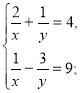
Друга пара – графічний метод
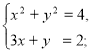
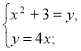
Третя пара – метод підстановки
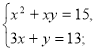
![]()
Четверта пара – метод заміни змінних
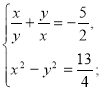
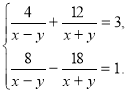
Історична довідка (презентація).
Те, що системи рівнянь другого степеня, можна використовувати в різних завданнях, помітили ще в давнину. У текстах, які були написані ще в III - II тисячоліттях до н.е., є чимало задач, які розв'язували за допомогою систем рівнянь.
Давньогрецький математик Діофант досліджував системи рівнянь другого степеня і розглядав різні варіанти розв'язування таких систем. Розглянуті їм методи можна використовувати для розв'язування рівнянь вищих ступенів.
Діофант Александрійський - видатний давньогрецький математик, який жив в Александрії. «Арифметика» Діофанта складалася з 13 книг, але збереглися тільки 6 перших. Велика частина праці - це збірник задач з розв'язками (збереглися 189 задач). На прикладах розв'язування задач автор демонстрував загальні методи. Діофант Діофант був настільки відомим математиком, що навіть епітафія на його могильному камені була написана у вигляді задачі. Там було зазначено: «Подорожній! Під цим каменем покоїться прах Діофанта, який помер в глибокій старості. Шосту частину довгого життя він був дитиною, дванадцяту - юнаком, сьому - провів неодруженим. Через п'ять років після одруження у нього народився син, який прожив удвічі менше батька. Через чотири роки після смерті сина заснув вічним сном і сам Діофант. Скажи, якщо вмієш рахувати, скільки років прожив Діофант? »
Графічний спосіб рівнянь вперше запропонував видатний французький філософ, математик, фізик, фізіолог Рене Декарт.
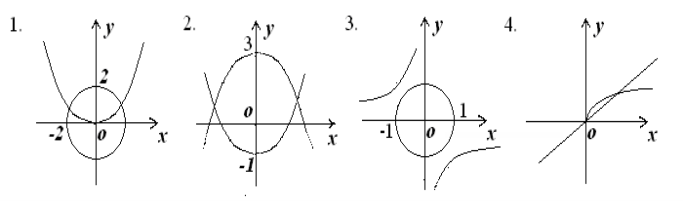
- Поставте відповідність між системами рівнянь із двома змінними та їх графіками.
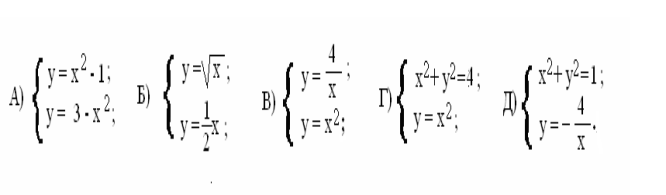
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
х |
|
|
2 |
х |
|
|
|
|
|
3 |
|
|
|
|
х |
|
4 |
|
х |
|
|
|
ІV. Рефлексивно-оцінювальний етап.
- Самооцінювання. Вправа «Мій діагноз»
- Сьогодні я дізнався…
- Було цікаво…
- Було складно…
- Я зрозумів, що…
- Тепер я зможу…
- Я навчився…
- У мене вийшло …
- Я зміг…
- Якщо сьогодні в когось щось не вийшло – не засмучуйтесь.
Головне – прагніть до нового.
Не махай на все рукою,
Не лінуйся, а учись.
Бо чого навчися в школі,
Знадобиться ще колись.
- Вправа «Мій настрій»
На початку уроку ми з вами зверталися до свого внутрішнього стану. Зробіть зараз те саме. Прикріпіть до деревинки листочок, що відповідає вашому настрою. Скажіть, у кого настрій після уроку став краще? У кого гіршим? Чому? У кого залишився таким самим?
Домашнє завдання
Використовуючи додаткові інформаційні джерела розв’язати систему рівнянь:
Метод почленного ділення рівнянь системи
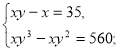
Метод алгебраїчного додавання
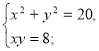


про публікацію авторської розробки
Додати розробку
