Урок – Challenge на тему "Нескінченно спадна геометрична прогресія", алгебра 9 клас

Комунальна організація (установа, заклад) «Шосткинський навчально-виховний комплекс: Шосткинська загальноосвітня школа І-ІІІ ступенів № 9 – дошкільний навчальний заклад Шосткинської міської ради Сумської області»

Урок – Challenge у 9 класі

 

Вчитель математики  Бондар Галина Михайлівна

Тема. Нескінченно спадна геометрична прогресія.

 

Мета: формувати поняття нескунченно спадної геометричної прогресії, вміння обчислювати суму нескінченної спадної геометричної прогресії, показати практичне застосування теми на прикладних задачах з використанням фракталів; розвивати вміння учнів створювати математичні моделі до розв'язування задач, уміння здійснювати дослідницьку діяльність та працювати з інформаційними джерелами; виховувати інтерес до математичних знань та їх практичного застосування; сприяти творчому розвитку, креативності.

Тип уроку: застосування набутих знань.

Інноваційна ідея: навчальний Challenge у напрямку зміни традиційного уявлення про математику з використанням хмарних сервісів.

Основні поняття, терміни: нескінченна спадна геометрична прогресія, геометричні фігури, площа, формули площ, подібність фігур.

Комплексне використання форм і методів: навчальний Challenge; використання хмарних сервісів Google: google.it (ментальна карта), Google Classroom (робота с медіа), goPollock (перевірка знань учнів), Google Blogger, Google Drive, LearningApps.org; діяльнісний метод; інтерактивні методи; робота в групах, інтергація навчальних предметів.

Обладнання: проектор, комп’ютери, смарфони, ноутбук, підручник, наочності. 

Хід уроку

Математика безмежно різноманітна, як світ, і присутня, міститься в усьому.

 М.П. Єругін

1.Організаційний момент.

#ШКОЛАХХІ

Школа ХХІ століття – це виклик, команда, підтримка, унікальність, розвиток, рух вперед.

 

#ОСВІТАCHALLENGE

https://padlet.com/galinabondar_13052012/afwkmjxvza92

Змінюємо традиційне уявлення про математику...
В природі є об’єкти, для опису форми яких евклідова геометрія безсила ...
Фрактали - революція в математичному описі об'єктів...
Прогресія - унікальне явище ....
Прогресія і фрактали ? Що спільного ?
Алгебра - це лише писана геометрія, а геометрія - зображена алгебра. 
                                                                                                          (Софі Жермен)

2. Перевірка домашнього завдання.

#МОЇЗНАННЯ

Майндмеппінг (mindmapping) - навчальний Challenge «Прогресії навколо нас» (експрес-огляд ментальної карти укладених задач практичного змісту з теми «Прогресії» у напрямку різних галузей та методів їх розв’язання).

Виконуючи домашнє завдання, ви переконалися, що прогресії застосовуються не тільки в математиці. За законом геометричної прогресії здійснюється поділ нейтронів під час ядерної ланцюгової реакції. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію. Геометрична прогресія відіграє велику роль у побудові математичних моделей економіки. Знання прогресій потрібні і в багатьох інших галузях.

 

3. Актуалізація опорних знань учнів.

#МОЇЗНАННЯ

Тестування з використанням сервісів goPollock,  LearningApps.org «Арифметична та геометричні прогресії».

Робота з тематичними флексагонами «Формули площ. Подібність» та LearningApps.org «Формули площ»

 

4. Мотивація навчальної діяльності учнів.

#МОЇМОТИВИ

Те, що ми знаємо – обмежено, а те чого не знаємо – нескінченне (П'єр-Симон Лаплас, французький математик і астроном)

Все, що створено людиною, обмежено площинами. Як описати форму хмар, узбережжя, крон дерев, сніжинок, кровоносної системи і системи альвеол людини або тварин. Де закінчуються правильні форми Евклідової геометрії, там зустрічаються фрактали. Актуальність уроку зумовлена практичним аспектом застосування набутих математичних знань у шкільному курсі (як з алгебри, так і з геометрії) до незвичних об’єктів, які зустрічаються у різних галузях (машинна графіка, фізика, хімія, біологія, радіотехніка, інформатика тощо).

Спробуємо змінити наше традиційне уявлення про математику.

 

5. Набуття нових знань.

 Тема «Нескінченна спадна геометрична прогресія»

Логічна послідовність: приклад, означення, формула суми нескінченної спадної геометричної прогресії.

Тема «Фрактали»

Група 1 «Дослідники»

Історичний аспект

 #ЦІКАВАІСТОРІЯ

Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як їм було дано таку назву. В роботах Рона Еглаша "Африканські Фрактали", задокументовано поширені фрактальні геометричні фігури в мистецтві тубільців. У 1525 році німецький митець Альбрехт Дюрер опублікував свою працю "Керівництво Художника", один із розділів якої має назву "Черепичні шаблони, утворені пентагонами". Джексон Поллок (американський експресіоніст 50-тих років) малював об'єкти, дуже схожі на фрактали. Лейбніц, Карл Веєрштрасс, Хельга Фон Кох, Поль П'єр Леві, Ґеорг Кантор, Анрі Пуанкаре, Феліксом Кляйном, П'єром Фату та Ґастоном Жюліа – досліджували ці унікальні фігури. Слово "фрактал" ввів в 1975 р. Б. Мандельброт.

Поняття фракталу.

#ЦІКАВЕПОНЯТТЯ

Унікальні об'єкти, породжені непередбачуваними рухами хаотичного миру, - це фрактали. Особливістю фракталів є не лише їх ламаність, а й самоподібність, яка полягає в тому, що кожна частина фрактала подібна цілому. Маленька гілочка – це крихітна подобудова великого дерева. Маленька хмарка являє собою щось на зразок великої хмари, а молекула – крихітний аналог галактики.

Види фракталів: «створені» (алгебраїчні, геометричні, стохастичні) та природні структури (фізичні).

Класифікація фрактальних множин

#ЦІКАВІВИДИ

Алгебраїчні фрактали - це найбільша група фракталів. Іх будують, використовуючи прості алгебраїчні формули. Якщо у прогресії 1,2,4,8,16,32,...,2ⁿ,2^n +1,… відкинути перші три члени, то отримаємо послідовність 8,16,32,...,2ⁿ,2^{n +1},..., яка також є геометричною прогресією, причому з тим же знаменником. Вона «подібна» вихідної прогресії з коефіцієнтом 8. Розглянемо таку геометрична прогресію: …, , , , 1, 3, 9, 27, … Помноживши кожен член цієї  прогресії на 3, отримаємо послідовність …, , , 1, 3, 9, 27, 81, …, яка виявилася тією ж самою прогресією.

Геометричні фрактали.

  Геометричні фрактали найнаочніші оскільки відразу видно самоподобність. У двомірному випадку їх отримують за допомогою деякої ламаної, званої генератором. За один крок алгоритму кожен з відрізків, складових ламаної, замінюється на ламану-генератор у відповідному масштабі. У результаті нескінченного повторення цієї процедури, виходить геометричний фрактал.

Геометричні фрактали мають колосальне практичне значення. На уроці ми будемо досліджувати трикутник Серпінського, килим Серпінського, серветку Коха, кругові фрактали, зірку Коха.

Стохастичні фрактали.

Фрактали, при побудові яких у ітеративної системі випадковим чином змінюються будь-які параметри. При цьому утворюються об’єкти  дуже схожі на природні – несиметричні дерева, порізані берегові лінії тощо.

 

5. Формування вмінь та навичок (розв’язування задач).

#МОЇВМІННЯ

Є в математиці щось таке, що викликає людське захоплення.                      (Ф. Хаусдорф)

Група 2 «Єксперти»

Задача 1

Задача французького математика Ніколя Орема (бл. 1323-1382). Обчислити площу фігури, утвореної з нескінченої множини прямокутників, якщо довжини горизонтальних сторін прямокутників зменшуються у відношенні 4:1, а довжини вертикальних – збільшуються у відношенні 1:2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

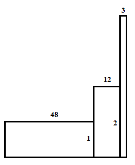
Розв’язання

Задача зводиться до обчислення суми членів нескінченно спадної геометричної прогресії:

Маємо:

.

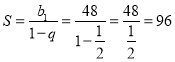Відповідь: 96.

 

Задача 2

Знайти площу трикутника Серпінського, якщо сторона початкового трикутника дорівнює α.

 

 

 

 

 

Використовуючи формулу площі рівностороннього трикутника маємо:

               

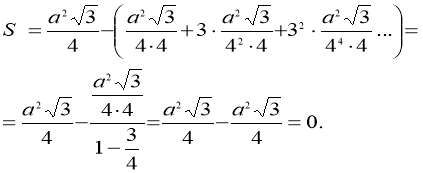
Трикутник Серпінського має нульову площу, оскільки в процесі побудови була виключена площа, в точності рівна площі вихідного трикутника.

Відповідь: 0.

Задача 3

Знайти площу килима Серпінського.

 

 

 

 

 

Нехай сторона початкового квадрата дорівнює 1. За формулою площі квадрата S = a² маємо:

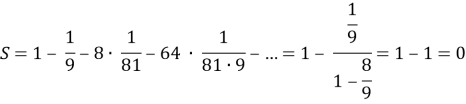
Відповідь : 0.

Задача 4

Знайти площу серветки Коха, якщо сторона початкового квадрата дорівнює 1.

 

 

 

 

 

 

За формулою S = a² та враховуючи, що послідовно приєднуються до даного одиничного квадрата, квадрати зі сторонами 1/3, 1/9, … маємо: 

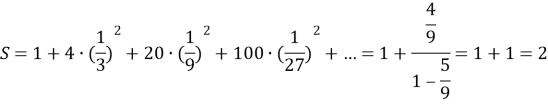
Відповідь: 2.

Задача 5

Знайдемо площу кругового фракталу, якщо радіус початкового круга дорівнює 1.

 

 

 

 

 

 

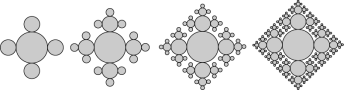
Послідовно приєднуємо до даного круга, круги радіусів ½, ¼, … . За формулою S = .

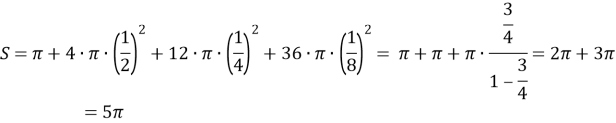
Задача 6

Площа зірки Коха

 

 

 

 

 

 

Зірка Коха повністю вміщується в круг, тому її площа заздалегідь обмежена. Нехай  площа початкового трикутника дорівнює 1. Використовуючи формулу площі  , знайдемо сторону початкового трикутника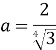 

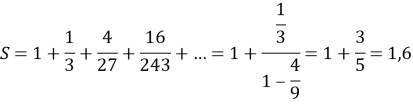
7.  Підсумок уроку. Рефлексія.

Навчальний Challenge «Чи змінили ви традиційне уявлення про математику?»  Чому ?

8. Оцінювання учнів.

Заповнення оціночних карток в групах.

9. Домашнє завдання.

Задача Побудуйте графік функції

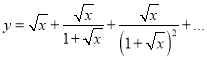, де  .