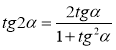Урок "Деякі способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших"
зміст
- Повторення курсу алгебри основної школи
- Числові множини. Множина дійсних чисел. Модуль дійсного числа та його властивості.
- Відсоткові розрахунки
- Числові функції. Область визначення і множина значень. Способи задання функцій
- Монотонність, парність, непарність функції. Огляд основних властивостей елементарних функцій
- Побудова графіків функцій за допомогою геометричних перетворень
- Побудова графіків функцій за допомогою геометричних перетворень
- Корінь п-го степеню, його властивості. Найпростіші перетворення радикалів
- Ірраціональні рівняння
- Системи ірраціональних рівнянь
- Степенева функція
- Показникова функція, її графік і властивості
- Показникова функція. Показникові рівняння
- Показникові нерівності
- Розв’язування вправ. Системи показникових рівнянь.
- Логарифм числа. Основні властивості логарифмів. Основна логарифмічна тотожність.
- Логарифмічна функція, її графік і властивості
- Логарифмічні рівняння
- Логарифмічні рівняння. Системи логарифмічних
- Логарифмічні нерівності
- Тригонометричні функції кута. Радіанна система вимірювання кутів і дуг
- Періодичність тригонометричних функцій
- Співвідношення між тригонометричними функціями одного аргументу
- Формули додавання. Тригонометричні функції подвійного і половинного аргументу.
- Формули перетворення суми у добуток
- Формули зведення
- Побудова графіків тригонометричних функцій
- Геометричні перетворення графіків тригонометричних функцій
- Поняття про обернену функцію. Обернені тригонометричні функції, їх властивості та побудова
- Розв’язування найпростіших тригонометричних рівнянь
- Деякі способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших………………………………………………………………………………………
- Практична робота
- Розв'язування тригонометричних нерівностей
ТЕМА УРОКУ
Повторення курсу алгебри основної школи
МЕТА УРОКУ
Дидактична:
- Систематизувати знання та навички студентів з розв’язування квадратних рівнянь та нерівностей, розв’язування систем рівнянь.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння «читати» графіки функцій.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
- Чому дорівнює квадрат суми (різниці) двох виразів?
![]()
- Чому дорівнює різниця квадратів?
![]()
- Чому дорівнює сума (різниця) кубів?
![]()
- Чому дорівнює куб суми (різниці) двох виразів?
![]()
- За якою формулою розкладається квадратний тричлен на множники?
![]() ,
,
де ![]() - корені відповідного квадратного рівняння.
- корені відповідного квадратного рівняння.
-
Як розв’язуються квадратні рівняння
 ?
?
![]()
![]()
![]()
![]() рівняння розв’язків не має.
рівняння розв’язків не має.
- Які квадратні рівняння називаються неповними?
|
|
|
|
|
|
|
|
|
|
|
|
ІІІ. Розв’язати рівняння.
1. ![]()
![]()
Відповідь: рівняння не має коренів.
2. ![]()
![]()
![]()
Відповідь: 0,5 та -3.
3. ![]()
|
|
або |
|
|
|
|
|
|
|
|
|
Відповідь: 2.
4. ![]()
![]()
![]()
Відповідь: ![]() .
.
5. ![]()
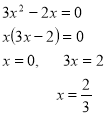
Відповідь: 0 та ![]() .
.
Приклади для самостійного виконання:
![]()
![]()
![]()
Як розв’язуються нерівності виду ![]() ?
?
Розглянемо можливі випадки розташування параболи відносно вісі Ох.

Розв’язати нерівність:
|
|
1. Розв’язати відповідне квадратне рівняння; корені – точки перетину з вісю Ох. |
|
|
2. Наносимо корені на вісь Ох і схематично будуємо параболу. |
|
Відповідь: |
3. В залежності від знаку даної нерівності записуємо відповідь. |
Що значить розв’язати систему рівнянь?
Знайти всі спільні корені даних рівнянь.
Приклад. 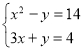
Розв’яжемо за допомогою методу алгебраїчного додавання
+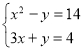
![]()
![]()
![]()
![]()
Відповідь: (3;-5), (-6;22).
Розв’яжемо дану систему графічним способом.
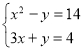
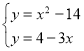

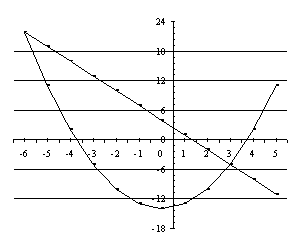
IV.Домашне завдання:
повторити означення функції, області визначення функції, області значень, класифікацію числових множин.
Розв’язати систему рівнянь
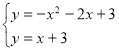
ТЕМА УРОКУ
Числові множини. Множина дійсних чисел. Модуль дійсного числа та його властивості.
МЕТА УРОКУ
Дидактична:
- Сформувати поняття множини;
- Сформувати вміння виконувати операції над множинами;
- Сформувати поняття числової множини, ознайомити з розширенням числових множин за рахунок множини дійсних чисел.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Множина - одне з найпростіших (первісних) математичних понять, яке не можна означити через інші, ще простіші поняття. Його можна пояснити тільки за допомогою рівнозначних понять або на окремих прикладах.
Під множиною розуміють сукупність об'єктів об'єднаних в цю сукупність за певними ознаками. Наприклад, можна говорити про множину студентів даного курсу.
Множини позначають великими буквами латинського і грецького алфавітів. Об'єкти, що входять до складу множини, називають її елементами і позначають малими буквами алфавіту. Задати множину - це означає задати характеристику її елементів, за допомогою якої про будь-який об'єкт можна встановити, належить він цій множині чи ні.
Якщо А - множина, а - її елемент, то це символічно записують:![]() і читають:а " належить "А.
і читають:а " належить "А.
Символічний запис![]() означає, що
означає, що ![]() не належить А.
не належить А.
Якщо множина містить безліч елементів, то її називають нескінченною, у противному разі - скінченою.
Якщо у множині немає жодного елемента , то її називають порожньою і позначають символом .
Для задання множини, утвореної з будь-яких елементів, будемо використовувати два такі способи.
В основі обох із них лежить позначення множини за допомогою фігурних дужок.
Приклад 1.1. Множина десяткових цифр записується {0,1,2,3,4,5,6,7,8,9}, множина основних арифметичних операцій - {+,-,*,/}.
Другий спосіб задання множин грунтується на зазначенні загальної властивості або породжувальної процедури для всіх об’єктів, що утворюють описувану множину.
Приклад 1.2.
S = { n , n - непарне число }
Дві множини A і B називаються рівними (записується A=B), якщо вони складаються з тих самих елементів.
Множина A називається підмножиною множини B (записується A![]() B ) тоді і тільки тоді, коли кожний елемент множини A належить також множині B. Кажуть також, що множина A міститься у множині B. Знак
B ) тоді і тільки тоді, коли кожний елемент множини A належить також множині B. Кажуть також, що множина A міститься у множині B. Знак![]() називають знаком включення.
називають знаком включення.
Для ілюстрації співвідношень між множинами використовують схеми, які називають діаграми Ейлера.
Для множини введемо такі операції.
Об'єднання множин. Нехай маємо дві множини А і В . Тоді множину яка містить у собі всі елементи множин А та В і не містить ніяких інших елементів, називають об'єднанням (сумою) множин А та В і записують: ![]() .
.

Приклад 1.3. {a,b,c} ![]() {a,c,d,e} = {a,b,c,d,e}.
{a,c,d,e} = {a,b,c,d,e}.

 Перетин множин. Нехай маємо дві множини А іВ. Тоді множину , яка містить всі спільні елементи множин А іВ і не містить ніяких інших елементів, називають перетином /добутком/ множин А іВ і записують:
Перетин множин. Нехай маємо дві множини А іВ. Тоді множину , яка містить всі спільні елементи множин А іВ і не містить ніяких інших елементів, називають перетином /добутком/ множин А іВ і записують: ![]() .
.
Приклад 1.4. {a,b,c}![]() {a,c,d,e} = {a,c},
{a,c,d,e} = {a,c},
{a,b,c}![]() {d,e} = .
{d,e} = .
Різницею множинA і B (записується A\B ) називається множина тих елементів, які належать множині A і не належать множині B.
Приклад 1.5. {a,b,c} \ {a,d,c} = {b},
{a,c,d,e} \ {a,b,c} = {d,e},
{a,b} \ {a,b,c,d} = .
Множина дійсних чисел
Для деяких множин у математиці вживаються сталі позначення.
Наприклад, ![]() - множина натуральних чисел,
- множина натуральних чисел,
![]() - множина цілих чисел,
- множина цілих чисел,
![]() - множина раціональних чисел,
- множина раціональних чисел,
R – множина дійсних чисел тощо.
Цілі та дробові числа як додатні, так і від'ємні, а також число нуль називаються раціональними числами.
Числа, виражені нескінченними неперіодичними десятковими дробами, називаються ірраціональними.
Сукупність раціональних та ірраціональних чисел - множиною дійсних чисел.



![]()
![]()
![]()
![]()
![]()
![]()
Основні властивості множини дійсних чисел відомі із шкільного курсу математики. Зупинимось докладніше на понятті абсолютної величини (модуля) дійсного числа.
Модулем дійсного числа![]() називається відстань від початку відліку до точки, яка зображує це число на координатній прямій.
називається відстань від початку відліку до точки, яка зображує це число на координатній прямій.
Модуль числа позначається символом![]() і за означенням
і за означенням ![]()
Властивості модуля:
-

-
 ,
, 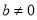
-
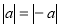
-

-

-
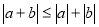 ,
, 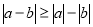
ІІІ. Вправи
- А – множина дільників числа 15; В – множина простих чисел, менших від 10; С- множина парних чисел, менших від 9. Укажіть елементи цих множин і знайдіть:
-
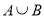 ;
;
-
 ;
;
-
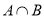 ;
;
-
 ;
;
-
 .
.
Розв’язання.
![]() ,
, ![]() ,
, ![]() .
.
-
 ;
;
-
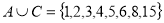
-
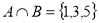
-
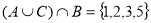
-
 .
.
-
Поставте замість зірочки знак
 або
або  так, щоб отримати правильне твердження:
так, щоб отримати правильне твердження:
1) 5*N; 2) -5*Q; 3) 3,14*Q; 4)1*R; 5) 0*N; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
3. Знайдіть множину спільних дільників числа 30 і 45.
![]()
4.Знайти значення виразу
![]() .
.
![]() .
.
ІV. Домашнє завдання:
Повторити: пропорція, відсоток від числа.
Обчислити ![]()
ТЕМА УРОКУ
Відсоткові розрахунки
МЕТА УРОКУ
Дидактична:
- Сформувати навички розв’язування задач на відсотки;
Розвиваюча:
- Розвивати усну і письмову культуру мовлення, логічнемислення, заохочувати студентів до самостійної навчальної діяльності;
Виховна:
- Виховувати допитливість, уважність, натхнення, любов до навчання та вміння працювати разом.
ТИП УРОКУ
Комбінований.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка домашнього завдання.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
Самостійна робота
|
Варіант 1 |
Варіант 2 |
|
1)Запишіть множину за допомогою перерахування її елементів: |
|
|
А) правильні дроби зі знаменником 6;
Б) розв’язки рівняння В) голосні звуки українського алфавіту. |
А) неправильні дроби зі чисельником 5;
Б) розв’язки рівняння В) дні тижня. |
|
2) Запишіть усі підмножини множини |
|
|
|
|
|
3) Серед наведених множин укажи порожню: |
|
|
А) множина прямокутних трикутників;
Б) множина розв’язків рівняння В) множина натуральних непарних чисел. |
А) множина рівнобічних трапецій;
Б) множина розв’язків рівняння В) множина від’ємних чисел, більших від нуля. |
|
4) Знайдіть |
|
|
|
|
|
5) Знайдіть множину розв’язків нерівності: |
|
|
|
|
ІІІ. Пропорцією називають рівність двох відношень:
![]() .
.
Числа ![]() називаються членами пропорції, причому а і d – крайніми, b і c– середніми членами.
називаються членами пропорції, причому а і d – крайніми, b і c– середніми членами.
Властивість пропорції:
![]() .
.
Приклад. Знайти х з пропорції:
![]() .
.
Відповідь: ![]() , х=25.
, х=25.
Відсоток — це однa сотa чaстинa від деякого цілого (1 % = 0,01).
Чaсто доводиться знaходити відсотки від числa. Для цього відсотки предстaвляємо десятковим дробом і множимо зaдaне число на одержaний дріб.
Нaприклaд, щоб знaйти 15 % від числа 40, предстaвляємо відсотки як 0,15 і множимо число 40 нa 0,15. Одержуємо число 6. Число 6 дорівнює 15 % від числa 40.
Щоб знaйти число зa його відсоткaми, требa відсотки предстaвити десятковим дробом і зaдaне число поділити на одержaний десятковий дріб. Одержимо число, відсотки якого були зaдaні.
Нaприклaд, відомо, що число 18 стaновить 40 % деякого числa. Щоб знaйти це число, поділимо 18 нa дріб, який відповідaє відсоткaм, тобто нa 0,4, і одержимо число 45. Число, 40 % якого дорівнюють числу 18, — це число 40.
Іноді потрібно знaходити відсоткове відношення. Щоб обчислити, скільки відсотків стaновить одне число від другого, требa поділити його нa число, відносно якого встaновлюють відсотки, і за одержaним десятковим дробом визнaчити відсотки.
Нaприклaд, щоб встaновити, скільки відсотків від числa 140 стaновить число 35, поділимо число 35 нa число 140, одержимо 0,25, що стaновить 25 %. Отже, число 35 стaновить 25 % від числa 140.
Формула складних відсотків:
![]()
![]() .
.
Наприклад. Перший внесок в банк дорівнює 300 доларів, за рік нараховується 3%. Знайти суму внеску через 5 років.
Розв’язання.
![]() доларів.
доларів.
Задача. Із кожної тони залізної руди можна видобути 620 кг заліза. Визначити відсотковий вміст заліза у цій руді.
Розв'язання. (620 : 1000)∙100% = 0,62∙100% = 62%.
Відповідь. 62%.
Задача .Картопля подешевшала на 20%. На скільки відсотків більше можна купити картоплі на ту саму суму?
Розв'язання.
Нехай треба купити1 кг картоплі і це коштує 100%=1. Після того як ціна знизилася на 20%, а кг картоплі можна купити за 80%=0,8.
Отже, можна скласти відсоткову пропорцію так: а кг картоплі коштує 0,8, тоді х кг картоплі коштує 1. Тобто, b:х = 0,8b:1, Звідси, маємо, х = 1,25 = 1 + 1/4. Тобто картоплі можна придбати на чверть більше, ¼ ∙ 100% = 25%.
Відповідь на 25% більше.
Задача . На скількивідсотківзбільшитьсяплоща квадрата, якщойого сторону збільшити на 20%.
Розв'язання. Початкова площа квадрата зі стороною а рівна а∙а, отже, після збільшення сторонни матимемо таку площу квадрата 1,2а∙1,2а = 1,44∙а∙а. Очевидно, що площа збільшилася на ( 1 - 1,44)∙100% = 44% .
Відповідь: площа збільшилася на 44% .
Задача . Перше число на 25% більше другого. На скільки відсотків друге число меншепершого?
Розв'язання. Якщо друге число 1а, то перше число 1, 25а. Складаємо пропорцію. Перше число 1,25а становить 100%, тоді друге число 1а становить х%. Звідси х = 1∙100:1,25 = 80%. Таким чином, 100% - 80% = 20%.
Відповідь: на 20%.
Задача . Латунь - сплав міді та цинку. Мідь складає 60% сплаву. Яке відсоткове відношення міді до цинку?
Розв'язання. 60:40 = 3:2 відношення міді до цинку. Отже, відношення цинку до міді 2:3, таким чином 200:3 = (66+ 2/3)%. А відношення міді до цинку (3:2)∙100 = 150%.
Відповідь: 150%.
ІV. Домашнє завдання:
Повторити: означення функції та її властивості, графіки основних видів функції.
ТЕМА УРОКУ
Числові функції. Область визначення і множина значень. Способи задання функцій
МЕТА УРОКУ
Дидактична:
- Систематизувати знання та навички про функції, їх властивості.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння «читати» графіки функцій.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
- Що називається функцією? Як позначають функцію?
Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у.
Позначають або однією літерою або f, F, або за допомогою рівності y=f(x).
- Що таке область визначення функції?
Множина значень, яких набуває незалежна змінна х, називається областю визначення функції.
- Що називається областю значень функції?
Множина відповідних значень залежної змінної у, яких вона набуває при всіх значеннях х з області визначення функції, називається областю значення функції.
- Назвіть основні способи задання функції:
Аналітичний (за допомогою формули), табличний, графічний.
- Чи будь-яка формула задає функцію?
Ні. Наприклад,
у=3 – функція,
х=5 – не є функцією, так як
єдиному значенню х (х=5)
відповідає нескінчена множина значень у.
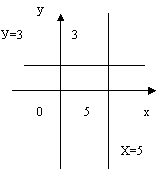
ІІІ.
- Яка функція називається зростаючою?
Функція y=f(x) називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції, тобто якщо ![]() , то
, то ![]() .
.
- Яка функція називається спадаючою?
Функція y=f(x) називається спадаючою, якщо більшому значенню аргументу відповідає менше значення функції, тобто якщо ![]() , то
, то ![]() .
.
- Яка функція називається парною?
Функція y=f(x) називається парною, якщо для будь-якого значення х з області визначення значення (-х) також належить області визначення і виконується рівність f(-x)=f(x).
- Яка функція називається непарною?
Функція y=f(x) називається непарною, якщо для будь-якого значення х з області визначення значення (-х) також належить області визначення і виконується рівність f(-x)= - f(x).
- Яка властивість графіків парної і непарної функцій вам відома?
Графік парної функції симетричний відносно вісі Оу, а непарної – відносно початку координат.
ІV. 1. Знайти область визначення функцій:
А) ![]() ; Б)
; Б) ![]() ;
;
В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
Розв’язання
А) ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Відповідь: ![]() .
.
 Б)
Б) ![]()
![]()
![]()
![]() ;
; ![]()
Відповідь: ![]()
2.Дослідити на парність і непарність функції:
А) ![]() ; Б)
; Б) ![]() ; в)
; в) ![]() ;
;
Г) ![]() ; Д)
; Д) ![]() ; е)
; е) ![]() .
.
Розв’язання
А) ![]() .
.
Значить, дана функція не є парною і не є непарною.
Б) ![]() - функція парна.
- функція парна.
Е) ![]() - функція непарна.
- функція непарна.
3. Знайдіть нулі і проміжки знакосталості функції:
А) ![]() Б)
Б) ![]() .
.
Розв’язання
 А)
А) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Відповідь: ![]() ;
; ![]() - нулі функції, у>0 при
- нулі функції, у>0 при ![]() ,
,
у<0 при![]() .
.
V. Домашнє завдання:
Вивчити конспект. Розвֺ’язати : 1 (в, д); 2(в, г); 3(б).
ТЕМА УРОКУ
Монотонність, парність, непарність функції. Огляд основних властивостей елементарних функцій
МЕТА УРОКУ
Дидактична:
- Систематизувати знання та навички про функції, їх властивості.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння «читати» графіки функцій.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Огляд основних видів функцій, їх властивостей та графіків
- Лінійна функція, її графік та властивості.
Функція виду ![]() , де х – незалежна змінна,
, де х – незалежна змінна, ![]() - довільні дійсні числа називається лінійною функцією.
- довільні дійсні числа називається лінійною функцією.
Графік лінійної функції – пряма.
Властивості:
-
-
Якщо
 , то
, то 
Якщо ![]() , то
, то ![]()
-
Якщо
 ,
, 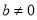 , то функція у – не є парною, не є непарною.
, то функція у – не є парною, не є непарною.
Якщо ![]() ,
, ![]() , то функція у – непарна.
, то функція у – непарна.
Якщо ![]() ,
, ![]() , то функція у – парна.
, то функція у – парна.
Якщо ![]() ,
, ![]() , то функція у – є парною і є непарною.
, то функція у – є парною і є непарною.
-
Якщо
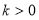 , , то функція у – зростає.
, , то функція у – зростає.
Якщо ![]() , , то функція у – спадає.
, , то функція у – спадає.
Якщо ![]() , , то функція у – стала.
, , то функція у – стала.

- Обернена пропорційність, , її графік та властивості.
Функція виду ![]() , де х – незалежна змінна,
, де х – незалежна змінна, ![]() - довільні дійсні числа (
- довільні дійсні числа (![]() ) називається оберненою пропорційністю.
) називається оберненою пропорційністю.
Графік оберненої пропорційності – гіпербола.
Властивості:
-

-

- Непарна.
-
Якщо
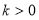 , , то функція у – спадає.
, , то функція у – спадає.
Якщо ![]() , , то функція у – зростає.
, , то функція у – зростає.

- Квадратичнафункція, її графік та властивості.
Функція виду ![]() , де х – незалежна змінна,
, де х – незалежна змінна, ![]() - довільні дійсні числа
- довільні дійсні числа ![]() називається лінійною функцією.
називається лінійною функцією.
Графік лінійної функції – парабола.
Властивості:
-
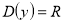
-
Якщо
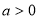 , то
, то  , де
, де 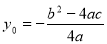 .
.
Якщо ![]() , то
, то ![]()
-
Якщо
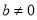 , то функція у – не є парною, не є непарною.
, то функція у – не є парною, не є непарною.
Якщо ![]() , то функція у – парна.
, то функція у – парна.
-
Якщо
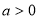 , , то функція у
, , то функція у при
при 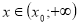
у![]() при
при ![]() ,
, ![]() .
.
-
Якщо
 , , то функція у
, , то функція у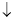 при
при 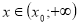
у![]() при
при ![]() .
.

![]()
![]()
![]()
ІІІ. Побудувати графіки функцій
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]()
Розв’язання.
|
x |
0 |
1 |
|
y |
-3 |
-1 |
![]() 1)
1) ![]() ; 2)
; 2) ![]() ;
;
![]()
![]()
![]()
![]()


![]() 3)
3) ![]() ;
;
![]()
![]()


![]() 4)
4) ![]() ;
;
![]()
![]()
 1)
1) ![]() ;
; 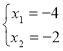
2) ![]() ;
; ![]()
3) ![]()
![]()
Вивчити конспект. Побудувати: ![]() .
.
ТЕМА УРОКУ
Побудова графіків функцій за допомогою геометричних перетворень
МЕТА УРОКУ
Дидактична:
- Систематизувати знання та навички про функції, їх властивості;
- Повторити види перетворень.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння будувати графіки функцій.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Які перетворення ви знаєте?
Симетрія відносно точки, симетрія відносно прямої, паралельне перенесення, поворот, деформація.
ІІІ.
|
Вид функції |
Перетворення |
Приклад |
|
|
Графік |
|
|
|
Графік функцій
|
|
|
|
Графік функцій |
|
|
|
Графік функцій |
|
|
|
Якщо k>1, то стиснути графік функцій |
|
|
Якщо 0<k<1, то розтягнути графік функцій |
|
|
|
|
Якщо k>1, то розтягнути графік функцій |
|
|
Якщо 0<k<1, то стиснути графік функцій |
|
ІV. № 1![]()
Алгоритм побудови:
-


-

 розтяг по вісі Оу в 2 рази
розтяг по вісі Оу в 2 рази
-

 симетрія відносно вісі Ох
симетрія відносно вісі Ох
-

 парал. перен. вгору на 1 од.
парал. перен. вгору на 1 од.

V. Домашнє завдання: Вивчити конспект.
ТЕМА УРОКУ
Побудова графіків функцій за допомогою геометричних перетворень
МЕТА УРОКУ
Дидактична:
- Систематизувати знання та навички про функції, їх властивості;
- Повторити види перетворень.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння будувати графіки функцій.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
Назвіть перетворення:
ІІІ. Побудуйте графіки функцій
№1
![]()
Алгоритм побудови:
-

-

 паралельне перенесення вліво на 2 од.
паралельне перенесення вліво на 2 од.
-

 симетрія відносно вісі Ох
симетрія відносно вісі Ох
-

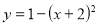 паралельне перенесення вгору на 1 од.
паралельне перенесення вгору на 1 од.

№ 2
![]()
Алгоритм побудови:
-

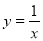
-

 парал. перен. вліво на 3 од.
парал. перен. вліво на 3 од.
-

 парал. перен. вниз на 4 од.
парал. перен. вниз на 4 од.

№ 3
![]()
Алгоритм побудови:
-


-

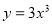 розтяг по вісі Оу в 3 рази
розтяг по вісі Оу в 3 рази
-

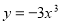 симетрія відносно вісі Ох
симетрія відносно вісі Ох
-

 парал. перен. вгору на 1 од.
парал. перен. вгору на 1 од.
№ 4
![]()
Алгоритм побудови:

№ 5
![]()
Виділимо повний квадрат
![]() А(1;-4) – вершина параболи
А(1;-4) – вершина параболи ![]() .
.
Алгоритм побудови:
-

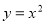 з вершиною в точці А(1;-4)
з вершиною в точці А(1;-4)
-

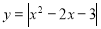 частину графіка, що знаходиться під Ох відобразити симетрично осі Ох.
частину графіка, що знаходиться під Ох відобразити симетрично осі Ох.

№ 6
![]()
Виділимо повний квадрат
![]() А(1;-4) – вершина параболи
А(1;-4) – вершина параболи ![]() .
.
Алгоритм побудови:
-

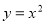 з вершиною в точці А(1;-4)
з вершиною в точці А(1;-4)
-

 частину графіка, що знаходиться праворуч від осі Оу відобразити симетрично вісі Оу.
частину графіка, що знаходиться праворуч від осі Оу відобразити симетрично вісі Оу.

ІV. Домашнє завдання:
Вивчити конспект. Побудувати:
у=-2(х+1)-3
![]()
![]()
ТЕМА УРОКУ
Корінь п-го степеню, його властивості. Найпростіші перетворення радикалів
МЕТА УРОКУ
Дидактична:
- На основі знань студентів про корінь квадратний ввести поняття кореня п-го степеня та узагальнити всі відомі їм властивості.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
- Що називається коренем квадратним з числа а?
Коренем квадратним з числа а називають число, квадрат якого дорівнює а.
![]()
- Що називається арифметичним коренем квадратним з числа а?
Арифметичним квадратним коренем з невід’ємного числа а є невід’ємне число, квадрат якого дорівнює а.
Розглянемо корінь будь-якого степеня з числа:
![]() - отже, число 5 є коренем кубічним з числа 125.
- отже, число 5 є коренем кубічним з числа 125.
![]() - число -4 є коренем кубічним з числа -64.
- число -4 є коренем кубічним з числа -64.
ІІІ. Коренем п-го степеня з числа а називається таке число, п-й степінь якого дорівнює а (![]() ).
).
Натуральні числа діляться на парні і непарні.
п-непарне: 1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
п- парне: 1) ![]() - два протилежні числа;
- два протилежні числа;
2) ![]() ;
;
3) ![]() - не існує.
- не існує.
Знак ![]() - називається радикалом.
- називається радикалом.
Арифметичним коренем п-го степеня з невід’ємного числа а називається невід’ємне число, п-й степінь якого дорівнює а (![]() ).
).
Властивості
-
Якщо
 , то
, то 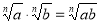 .
.
-
Якщо
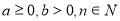 , то
, то 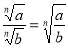 .
.
-
Якщо
 , то
, то  .
.
-
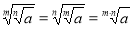 .
.
-
 .
.
З радикалами можна виконувати наступні дії.
- Винесення множника з під знака радикала.
![]() ;
;
![]() ;
;
![]() .
.
- Внесення додатніх множників під знак радикала.
![]()
- Зведення радикала до найпростішого (нормального) вигляду.
Радикал зведений до найпростішого вигляду коли: підкореневий вираз не містить дробів; раціональні множники винесені за знак радикала; показник кореня та показник степеня підкореневого виразу скорочені.
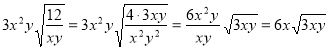 ;
;
![]() .
.
- Зведення подібних радикалів.
Радикали називаються подібними, якщо після зведення їх до найпростішого вигляду вони мають рівні підкореневі вирази і однакові показники.
Множник, що стоїть перед знаком радикала, називається коефіцієнтом.
- Дії над радикалами.
![]() ;
;
![]() ;
;
![]() .
.
ІV. № 1
Знайти значення:
-
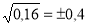 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 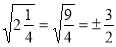 ;
;
5) ![]() .
.
№ 2 Знайти значення виразу:
1) ![]() ;
;
2) ![]() .
.
№ 3 Знайти невідому:

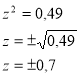
№ 4 При яких значеннях а і х мають зміст вирази:
1)![]() при
при ![]() ; 2)
; 2) ![]() при
при ![]() ;
;
3) ![]() при
при ![]() ; 4)
; 4) ![]() при
при ![]() ;
;
5) ![]() при
при ![]() ; 6)
; 6) ![]() при
при ![]() .
.
№ 5 Знайти значення виразів:
![]() ;
;
![]() ;
;
![]() .
.
№ 6 Спростити вираз:
![]() .
.
№ 7 Обчислити:
![]() .
.
№ 7 Винести множник за знак радикала:
![]() .
.
№ 8 Звести до найпростішого вигляду:
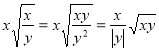 ;
;

- Домашнє завдання:
Винести множник за знак радикала:
![]() ;
; ![]() ;
; ![]()
Скоротіть дріб:
![]() ;
; ![]() .
.
ТЕМА УРОКУ
Ірраціональні рівняння
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «ірраціональні рівняння» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. 2 студенти біля дошки показують розв’язання д/з.
Фронтальне опитування:
- Що називається коренем n – го степеня з числа а?
- Що називається коренем арифметичним?
-
Які властивості має
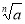 .
.
- Які числа називаються ірраціональними?
Числа, виражені нескінченними неперіодичними десятковими дробами, називаються ірраціональними.
ІІІ. Рівняння, в яких невідоме міститься під знаком кореня, називають ірраціональними.
Приклади Контрприклади
![]()
![]()
![]()
![]()
![]()
Ірраціональні рівняння розв’язуються шляхом піднесення обох частин рівняння до n – гостепеня (n – залежить від рівняння).
В ірраціональних рівняннях обов’язково робиться перевірка, так як при піднесені до парного степеня ми розширюємо область допустимих значень рівняння.
Наприклад, ![]() Перевірка
Перевірка
![]()
![]()
![]()
![]()
![]() 5=5
5=5
ІV. Розв’язати рівняння:
1) ![]() Перевірка
Перевірка
2-х=3-2х ![]()
2х-х=3-2 ![]()
х=1 1=1
2) ![]()

![]()
![]()
Перевірка
![]()
![]()
![]()
![]()
![]() 1=1
1=1
Відповідь: ![]() .
.
3) ![]()
![]()
Введемо заміну ![]()
Тоді ![]()
![]()
![]()
Підставимо в рівняння заміни
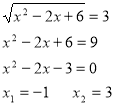
Значення -4 не підходить.
Перевірка
![]()
5=5
![]()
9=9
Відповідь: ![]() .
.
4) ![]()
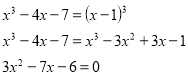
![]()
![]()
Перевірка
![]()
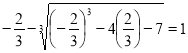
3-2=1 ![]()
1=1 1=1
Відповідь: ![]() .
.
- Розв’яжіть рівняння:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
VІ.Домашнє завдання : конспект, приклади (1,3,6).
ТЕМА УРОКУ
Системи ірраціональних рівнянь
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «системи ірраціональних рівнянь» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ.
При розв’язувані систем ірраціональних рівнянь використовуються ті самі методи, що і при розв’язанні систем лінійних рівнянь (метод підстановки, алгебраїчного додавання).
Особливістю розв’язання систем ірраціональних рівнянь є необхідність знаходження ОДЗ системи або перевірка отриманих значень невідомих.
ІІІ. Наприклад,
1.  ;
; 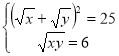 ;
; 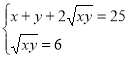 ;
; ![]() ;
; ![]() ;
;
![]() ;
;

![]() ;
;
![]()
ОДЗ: ![]() Відповідь: (9;4), (4;9).
Відповідь: (9;4), (4;9).
ІV.
№1. Розв’язати системи рівнянь:
а) ![]()
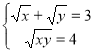 ; б)
; б)  ; в)
; в)  ;
;
б)  ;
;
 ;
;  ;
;  ;
; ![]()
![]() ОДЗ:
ОДЗ: ![]()
Відповідь: (5;20), (20;5).
2.  ;
;
Розв’язання
Скористаємося формулою ![]() ;
;
 ;
; 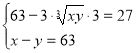 ;
;  ;
; 
![]()
![]()
![]()
![]()
![]() ОДЗ:
ОДЗ: ![]()
Відповідь: (1;64), (-64;-1).
№ 2. Розв’язати системи рівнянь:
а)  ; б)
; б)  ; в)
; в) 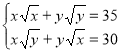 ; г)
; г) 
в) 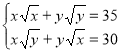
Розв’язання
Введемо позначення 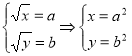 , тоді маємо
, тоді маємо
 Помножимо друге рівняння на 3 і додамо обидва рівняння.
Помножимо друге рівняння на 3 і додамо обидва рівняння.
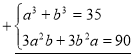
![]()
![]()
![]()
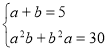 ;
; ![]() ;
; ![]() ;
; ![]() ;
; 
Зробимо зворотну підстановку
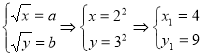 ;
; 
ОДЗ: ![]() Відповідь: (9;4), (4;9).
Відповідь: (9;4), (4;9).
V. Домашнє завдання:
Вивчити конспект. № 1(в), №2(б, г).
ТЕМА УРОКУ
Степінь з раціональним показниками та її властивості
МЕТА УРОКУ
Дидактична:
- Формування поняття степеня з раціональним показником, степінь з ірраціональним показником.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
1. Відповіді на запитання, що виникли в учнів при розв'язуванні домашнього завдання.
2. Колективне розв'язування нерівності ![]() < 4 – х.
< 4 – х.
Відповідь: 0 < х < 2.
II. Повторення і систематизація знань учнів про степінь з натуральним і цілим показником.
Повторення і систематизацію знань учнів про степінь із натуральним і цілим показником рекомендується провести шляхом бесіди з використанням таблиці 17.
Питання до класу:
1. Що називається n-м степенем числа а, якщо п ![]() N? якщо п = 1? п = 0?
N? якщо п = 1? п = 0?
2. Що таке степінь, основа степеня, показник степеня?
3. Що називається n-м степенем числа а, якщо п ![]() Z?
Z?
4. Сформулюйте основні властивості степенів.
Таблиця 17
|
Степені
|
|
|
з натуральним показником:
а1 = а (а
аn = а · а · ... · а п
|
з цілим показником а0 = 1, а ≠ 0
а-n =
|
|
Властивості аm · аn = am + n аm : аn = am – n (аm)n = аmn (аb)n = anbn
|
|
III. Формування поняття степеня з дробовим показником.
Введемо поняття степеня з дробовим показником. Вводячи це поняття, хотілося би, щоб степінь з раціональним показником мав ті самі властивості, що й степінь із цілим показником. Зокрема, n-й степінь числа ![]() повинен дорівнювати аm. Якщо ця властивість виконується, то
повинен дорівнювати аm. Якщо ця властивість виконується, то  – а це означає (за означенням кореня п-го степеня), що число
– а це означає (за означенням кореня п-го степеня), що число ![]() повинно бути коренем п-го степеня із числа аn.
повинно бути коренем п-го степеня із числа аn.
!
Степенем ![]() числа а > 0 з раціональним показником
числа а > 0 з раціональним показником ![]() , де m
, де m![]() Z, п
Z, п![]() N (п>1) називається число
N (п>1) називається число ![]() .
.
Отже, ![]() =
= ![]() .
.
Степінь числа 0 визначений тільки для додатних показників;
за означенням (0r = 0 для будь-якого г > 0.
Виконання вправ
1. Подайте вирази у вигляді степеня з раціональним показником:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Подайте вирази у вигляді кореня із числа чи виразу:
а) ![]() ; б) 5
; б) 5![]() ; в) 6
; в) 6![]() ; г) 3
; г) 3![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Обчисліть:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Відповідь: а) 3; б) 3; в) 4; г) 27.
IV. Вивчення властивостей степенів з раціональним показником.
Для будь-яких раціональних чисел р і q і будь-яких додатних а і b справедливі рівності:
|
аp · аq = ap +qn; аp : аq = ap – q ; (аp)q = аpq ; (аb)p = apbp;
|
Для доведення цих властивостей треба скористатися означенням степеня з раціональним показником і властивостями коренів. Доведемо першу рівність: нехай ![]() ,
, ![]() , тоді
, тоді
![]() Останні рівності доводяться аналогічно.
Останні рівності доводяться аналогічно.
Виконання вправ № 99 (2), 100 (2), 101 (2), 103 (3, 4).______
V. Сприймання поняття про степінь з ірраціональним показником.
Розглянемо степінь ![]() з ірраціональним показником
з ірраціональним показником ![]() . Ірраціональне число
. Ірраціональне число ![]() можна подати у вигляді нескінченного неперіодичного десяткового дробу.
можна подати у вигляді нескінченного неперіодичного десяткового дробу.
Розглянемо послідовність наближень числа ![]() :
:
1 < ![]() < 2,
< 2,
1,4 < ![]() < 1,5,
< 1,5,
1,41 < ![]() < 1,42,
< 1,42,
1,414 < ![]() < 1,415,
< 1,415,
1,4142 < ![]() < 1,4143,
< 1,4143,
…
За допомогою калькулятора знайдемо наближені значення степенів числа 10 з недостачею і надлишком, тоді матимемо:
10 = 101 < ![]() < 102 = 100,
< 102 = 100,
25,119 ![]() 101,4 <
101,4 < ![]() < 101,5
< 101,5 ![]() 31,623,
31,623,
25,704 ![]() 101,41 <
101,41 < ![]() < 101,42
< 101,42 ![]() 26,303,
26,303,
25,942 ![]() 101,414 <
101,414 < ![]() < 101,415
< 101,415 ![]() 26,002 ,
26,002 ,
25,953 ![]() 101,4142 <
101,4142 < ![]() < 101,4143
< 101,4143 ![]() 25,960 ,
25,960 ,
Наведені значення з недостачею і надлишком наближаються до одного і того самого числа ![]() = 25,9..., яке і прийнято вважати степенем числа 10 з показником
= 25,9..., яке і прийнято вважати степенем числа 10 з показником ![]() .
.
Таким чином, ми розширили поняття степеня на будь-які дійсні показники, зберігаючи при цьому властивості степенів.
VI. Підведення підсумків уроку.
VII. Домашнє завдання.
Розділ III § 3 (1—3). Запитання і завдання для повторення до розділу III № 56—66. Вправи №№ 99 (1), 100 (1), 103 (1, 2).
ТЕМА УРОКУ
Степенева функція
МЕТА УРОКУ
Дидактична:
Познайомити учнів із степеневою функцією, її властивостями і графіками
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Перевірка домашнього завдання.
1. Перевірити наявність виконаного домашнього завдання.
2. Розв'язування вправ.
а) Обчислити ![]() . Відповідь: 5.
. Відповідь: 5.
б) Спростити вираз  . Відповідь: ab.
. Відповідь: ab.
в) Спростити вираз 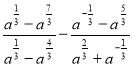 . Відповідь: 2a.
. Відповідь: 2a.
II. Сприймання і усвідомлення матеріалу про степеневу функцію.
Степеневою функцією називається функція виду у = хp, де р — постійне дійсне число, а х (основа) — змінна. Згадаємо властивості степеневих функцій, їхні графіки. Результати наших досліджень будемо записувати в таблицю 18.
Таблиця 18
Функція у = хp
|
|
p |
Графік |
D(y) |
E(y) |
Парність (непарність) |
Зростання (спадання) |
||
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
||
|
1. |
p=2k,
k
|
|
R |
[0; + |
парна |
спадає, якщо
х
якщо х |
||
|
2. |
p=2k+1
k |
|
R |
R |
непарна |
зростає |
||
|
3. |
p=-(2k),
k |
|
x ≠ 0 |
(0; + |
парна |
зростає, якщо
х
якщо х |
||
|
4.
|
p=-(2k-1)
k |
|
x ≠ 0 |
y ≠ 0 |
непарна |
спадає
на проміжках (-
(0; + |
||
|
5. |
p > 0, p – не ціле, 0<р<1 |
|
[0;+ |
[0;+ |
ні парна, ні непарна |
зростає |
||
|
6. |
Р>0, p – не ціле, р > 1 |
|
[0;+ |
[0;+ |
ні парна, ні непарна |
зростає |
||
|
7. |
р < 0, р – не ціле |
|
(0;+ |
(0;+ |
ні парна, ні непарна |
спадає |
||
1. Якщо р = 2k, k ![]() Z, то функція у = х2k. Якщо k = 1, то ця функція має вигляд у = х2. Згадаємо її основні властивості. Функція у = х2:
Z, то функція у = х2k. Якщо k = 1, то ця функція має вигляд у = х2. Згадаємо її основні властивості. Функція у = х2:
- визначена для будь-якого дійсного х;
- додатна при х ≠ 0 і дорівнює 0 при х = 0;
- приймає всі невід'ємні значення;
- парна (графік симетричний відносно осі OY);
-
спадає, якщо х є (-
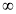 ; 0] і зростає, якщо х є [0; +
; 0] і зростає, якщо х є [0; +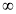 ). Такі саме властивості має. функція у = х2k (рис. 80 підручника).
). Такі саме властивості має. функція у = х2k (рис. 80 підручника).
2. Якщо р = 1, то функція має вигляд у = х (графік — пряма, що проходить через початок координат і ділить перший і третій координатний кути пополам). Якщо р = 3, то ця функція має вигляд у = х3. Функція у = х3:
- визначена для будь-якого дійсного х;
- додатна при х > 0, від'ємна при х < 0 і дорівнює 0 при х = 0;
- зростаюча;
- приймає всі дійсні значення;
-
непарна (графік симетричний відносно початку координат), Такі самі властивості має степенева функція у = х2k+1, k
 N (рис. 79 підручника).
N (рис. 79 підручника).
3. Розглянемо функцію у = ![]() . Ця функція визначена при х ≠ 0 і приймає всі додатні значення. Функція парна (графік симетричний відносно осі OY). При х < 0 функція зростає, а при х > 0 — спадає. Такі саме властивості має степенева функція у = х-2k =
. Ця функція визначена при х ≠ 0 і приймає всі додатні значення. Функція парна (графік симетричний відносно осі OY). При х < 0 функція зростає, а при х > 0 — спадає. Такі саме властивості має степенева функція у = х-2k =![]() , k
, k ![]() N (рис. 82 підручника).
N (рис. 82 підручника).
4. Якщо р = – 1, то функція має вигляд у = х-1 = ![]() . Ця функція визначена при х ≠ 0. При х > 0 функція у =
. Ця функція визначена при х ≠ 0. При х > 0 функція у = ![]() приймає додатні значення, а при х < 0 — від'ємні. При х > 0 функція у =
приймає додатні значення, а при х < 0 — від'ємні. При х > 0 функція у = ![]() спадає, і при х < 0 — спадає.
спадає, і при х < 0 — спадає.
Такі саме властивості має степенева функція у = х – (2k – 1) = ![]() , k
, k ![]() N (рис. 81 підручника).
N (рис. 81 підручника).
5-6. Згадаємо властивості функції у = ![]() . Отже, функція у =
. Отже, функція у = ![]() :
:
- визначена при х > 0;
- додатна при х > О і дорівнює нулю при х = 0;
- зростає на всій області визначення;
- приймає всі невід'ємні значення.
Якщо р — додатне раціональне число, то степенева функція у = xp визначена при х ![]() 0 і має такі саме властивості, які функція у =
0 і має такі саме властивості, які функція у = ![]() .
.
III. Осмислення вивченого матеріалу.
Виконання № 78—85 із «Запитання і завдання для повторення» розділу III.
IV. Підсумок уроку.
V. Домашнє завдання.
Розділ III § 3(4). Запитання і завдання для повторення розділу III. № 67—77.
ТЕМА УРОКУ
Показникова функція, її графік і властивості
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «показникові функція»
- Засвоєння учнями поняття показникової функції, її властивостей і графіка.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
II. Повідомлення теми уроку.
III. Сприймання і усвідомлення нового матеріалу.
!
Функція виду у = ах, де а > 0, а ≠ 1, називається показниковою (з основою а).
Усне виконання вправ
1. Які із поданих функцій є показниковими:
а) у = 2х; б) у = х3; в) у = (-5)х; г) у = (![]() )х; д) у = (0,3)х; е) у = πх?
)х; д) у = (0,3)х; е) у = πх?
Відповідь: а); г); д); е).
2. Наведіть приклади показникових функцій.
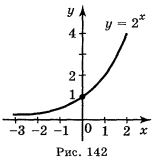 Почнемо вивчення показникових функцій з функції у = 2х. Складемо таблицю значень функції:
Почнемо вивчення показникових функцій з функції у = 2х. Складемо таблицю значень функції:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у = 2х |
|
|
|
1 |
2 |
4 |
8 |
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у = 2х (рис. 142).
Показникова функція у = 2х має властивості:
1. Область визначення — множина всіх дійсних чисел.
2. Область значень — множина всіх додатних чисел.
3. Функція у = 2х — зростаюча на множині всіх дійсних чисел.
4. Графік функції перетинає вісь у в точці(0; 1).
Усне виконання вправ
1. Чи є серед значень функції у = 2х:
а) найбільше; б) найменше? Відповідь: ні.
2. Порівняйте значення виразів:
а) ![]() і
і ![]() ; б) 2-3 і 2-4; в)
; б) 2-3 і 2-4; в) ![]() і
і ![]() .
.
Відповідь: а) ![]() <
< ![]() ; б) 2-3 > 2-4; в)
; б) 2-3 > 2-4; в) ![]() >
> ![]() .
.
3. Розташуйте числа ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() у порядку зростання.
у порядку зростання.
Відповідь: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
4. Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 2х > 2у; б) 2х < 2у. Відповідь: а) х > у; б) х < у.
5. На рисунку 86 із підручника зображено графіки функцій у = 2х і у = 3х. Чим відрізняються ці функції? Їхні графіки?
Відповідь: ці функції мають одинакові властивості, функція у = 3х зростає більш швидше (графік цієї функції піднімається вгору більш круто).
Побудуємо графік функції у = ![]() , для цього складемо таблицю значень функції:
, для цього складемо таблицю значень функції:
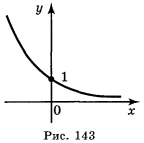 Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у =
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у = ![]() (рис. 143). Сформулюємо властивості функції
(рис. 143). Сформулюємо властивості функції
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у = |
8 |
4 |
2 |
1 |
|
|
|
1. Область визначення — множина всіх дійсних чисел.
2. Область значень — множина всіх додатних чисел.
3. Функція у = ![]() — спадна на множині всіх дійсних чисел.
— спадна на множині всіх дійсних чисел.
4. Графік функції перетинає вісь у в точці (0; 1).
Усне виконання вправ
1. Чи є серед всіх значень функції у = ![]() :
:
а) найменше; б) найбільше? Відповідь: ні.
2. Порівняйте значення виразів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() .
.
Відповідь:
а) ![]() >
>![]() ; б)
; б) ![]() =
=![]() ; в)
; в) ![]() >
>![]() ; г)
; г) ![]() <
<![]() ; д)
; д) ![]() <
<![]() .
.
3. Розташуйте числа ![]() ,
, ![]() ,
,  ,
, 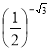 ,
, ![]() у порядку зростання.
у порядку зростання.
Відповідь: ![]() ,
, ![]() ,
,  ,
, 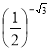 ,
, ![]() .
.
4. Порівняйте х і у, якщо відомо, що вірна нерівність: а)![]() >
>![]() ; б)
; б)![]() >
>![]() ;
;
Відповідь: а) х < у; б) х > у.
5. Порівняйте як розташовані графіки функцій у = 2х і у = ![]() , користуючись рис. 88 із підручника.
, користуючись рис. 88 із підручника.
Відповідь: графіки розташовані симетрично відносно осі ОY.
6. Чим відрізняються властивості і графіки функцій у =![]() і у=
і у= ![]() ?
?
Відповідь: вони мають однакові властивості, функція у = ![]() спадає більш швидше.
спадає більш швидше.
IV. Систематизація і осмислення вивченого матеріалу.
Враховуючи вищезазначене, можна зробити висновки.
1. Область визначення показникової функції — множина R дійсних чисел, бо степінь aх, де а > 0, визначений для всіх х ![]() R.
R.
2. Множина значень показникової функції — множина всіх додатних дійсних чисел.
3. Показникова функція у = aх є зростаючою на множині дійсних чисел, якщо а > 1, і спадною, якщо 0 < а < 1.
4. Якщо х = 0, то у = а° = 1.
5. Якщо х > 0, то у > 1, якщо а > 1, і у < 1, якщо 0 < а < 1.
6. Якщо х < 0, то у < 1, якщо а > 1, і у > 1, якщо 0 < а < 1.
7. Графіком показникової функції є крива, яка називається експонентою.
Властивості показникової функції записати в робочому зошиті у вигляді таблиці 19.
Таблиця 19
|
Показникова функція у = ах, а > 0, а ≠ 1
|
|
|
а > 1 |
0 < а < 1 |
|
1. D(y) = R
2. Е(у) = (0; + 3. Зростає
x1 > x2 4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у < 1 6. Якщо х > 0, то у > 1
|
1. D(y) = R
2. E(y) = (0; + 3. Спадає
x1 > x2 4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у > 1 6. Якщо х > 0, то у < 1
|
Усне виконання вправ
1. Які з наведених показникових функцій є зростаючими, а які — спадними:
а) y = πx ; б) y = (0,5)x; в) у = ![]() ; г) y = 2-x.
; г) y = 2-x.
Відповідь: а) зростаюча; б) спадна; в) зростаюча; г) спадна.
2. Порівняйте значення виразів:
а) ![]() i
i ![]() ; б)
; б) 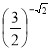 і
і  .
.
Відповідь: а) ![]() >
> ![]() ; б)
; б) 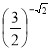 >
>  .
.
3. Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 0,02х < 0,02y; б) πx > πy.
Відповідь: а) х > у; б) x < у.
4. Порівняйте основу а > 0 з одиницею, якщо відомо, що вірна нерівність:
а) а10 > а15; б) а10 < а15.
Відповідь: а) а > 1; б) 0 < а < 1.
V. Підсумок уроку.
VI. Домашнє завдання.
Розділ IV § 1. Запитання і завдання для повторення № 1—12.
ТЕМА УРОКУ
Показникова функція. Показникові рівняння
МЕТА УРОКУ
Дидактична:
- Сформувати поняття показникові функція показникові рівняння;
- Сформувати вміння виконувати побудову графіка показникової функції;
- Розглянути методи розв’язання показникових рівнянь.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Повідомлення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Повторюю з студентами означення функції та перераховуємо властивості функції.
ІІІ. Функція ![]() , де
, де ![]()
![]() називається показниковою функкцією з основою a.
називається показниковою функкцією з основою a.
Побудуємо графіки функцій ![]() та
та 
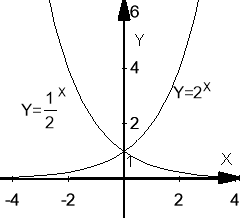
Властивості
1) D(y)=R
2) E(y)=(o;+![]() )
)
3) не є парною, не є непарною
4) неперіодична
5) При a>1, y![]()
При a<1, y![]()
Якщо a>0. a![]() ,
, ![]() то
то ![]() тобто, якщо степінь однієї, і тієї самої додатньої, відміної від одиниці основи, рівні, то рівні й показники степеня.
тобто, якщо степінь однієї, і тієї самої додатньої, відміної від одиниці основи, рівні, то рівні й показники степеня.
Якщо a>0, і ![]() то яке б не було додатнє число N, існує і до того ж єдине таке значення x, що
то яке б не було додатнє число N, існує і до того ж єдине таке значення x, що ![]()
Показникові рівняння
Показниковими називається рівняння, в яких невідоме входить лише де показників степенів при сталих основах.
Види рівнянь
1)![]()
![]()
2)![]()
Способи розв’язування
1) Зведення до однієї основи
№1
2) ![]() 3) 2
3) 2![]() 6)
6) ![]()
![]()



9) ![]()
![]()
![]()
![]() або
або ![]()
![]()
![]()
2) Зведення до спільного показника
№1 10) ![]()
![]()
![]()
![]()
3) Винесення спільного множника за дужки
№ 1 14) ![]()
![]()
![]()
![]()
![]()
4) Розв’язання рівнянь зводячи їх до виду ![]()
№ 1 15) ![]()
![]()
![]()
![]() - не задовольняє означенню
- не задовольняє означенню
![]()
![]()
![]()
ІV. № 1
5) ![]()
8) ![]()
13) ![]()
16) ![]()
24) ![]()
21) ![]()
17) ![]()
33) ![]()
V. Д/з. Стор. 201 № 1 (25,28,37,32).
ТЕМА УРОКУ
Показникові нерівності
МЕТА УРОКУ
Дидактична:
- Формування умінь учнів розв'язувати показникові нерівності
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Повідомлення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх. Перевірка домашнього завдання.
1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань.
2. Усне розв'язування показникових нерівностей з використанням таблиці 21 для усних обчислень «Показникові нерівності ».
Таблиця 21
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
2х > 8 |
|
|
|
2х > -2 |
|
2 |
2х < -2 |
3х |
|
|
|
|
3 |
|
|
|
0,2х |
7х > 1 |
|
4 |
103х |
2х < 0,25 |
5х |
|
|
|
5 |
|
|
|
|
|
II. Формування умінь розв'язувати показникові нерівності.
Розглянемо показникову нерівність виду
![]()
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Наприклад,
№2 1) ![]() ; 2)
; 2) ![]() 3)
3) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
![]() Відповідь:
Відповідь: ![]()
![]()
Відповідь: ![]()
V. Розв’язати нерівності:
 4)
4)  ;
;
![]()
![]()
![]()
Відповідь: ![]()
5) ![]() ;
;
![]()
![]()
![]()
Відповідь: ![]() .
.
|
14)
Відповідь: |
24)
Відповідь: |
|
29)
Нехай
Відповідь: |
|
|
32)
Відповідь: |
35)
Відповідь: |
III. Самостійна робота.
Варіант 1.
Розв’яжіть нерівність:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Варіант 2.
Розв’яжіть нерівність:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Відповідь: В-1. а) (0;+![]() ); б) (-2;2); в) х – будь-яке; г) (2;+
); б) (-2;2); в) х – будь-яке; г) (2;+![]() ).
).
В-2. а) (0;+![]() ); б) (-
); б) (-![]() ;-1)
;-1)![]() (1;+
(1;+![]() ); в) х – будь-яке; г) (2;+
); в) х – будь-яке; г) (2;+![]() ).
).
IV. Підведення підсумків уроку.
Д/з. Шкіль ст.. 202 №2(25, 6, 8, 12, 33)
ТЕМА УРОКУ
Розв’язування вправ. Системи показникових рівнянь.
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «показниковы рівняння та їх системи» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ.
1. Розв’язати систему рівнянь:
1) 


Нехай ![]() , тоді
, тоді ![]() ,
,
![]()
![]()
Зворотна підстановка ![]()
![]() .
.
![]() .
.
Відповідь: (4;5), (5;4).
III. Розв'язування систем логарифмічних рівнянь.
При розв'язуванні систем показникових рівнянь використовують ті саме способи, що й при розв'язуванні алгебраїчних систем. Розглянемо приклади.
Приклад 1. Розв'яжіть систему рівнянь: 
Розв'язання
Помножимо почленно рівняння системи, тоді одержимо:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
підставимо в будь-яке рівняння системи і отримаємо
![]()
 ,
, ![]() .
.
![]()
Відповідь: (2; 1).
Приклад 2. Розв'яжіть систему рівнянь 
Розв'язання

Нехай ![]() , тоді
, тоді ![]() ,
,
![]()
![]()
Зворотна підстановка ![]()
![]() .
.
![]() .
.
Відповідь: (2;1), (7;![]() ).
).
IV. Формування умінь розв'язувати системи показникових рівнянь.
Розв'язування вправ
1) 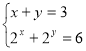 2)
2) 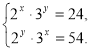 3)
3) 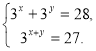
V. Підведення підсумків уроку.
VI. Домашнє завдання. Конспект.
ТЕМА УРОКУ
Розв’язування вправ. Системи показникових рівнянь
МЕТА УРОКУ
Дидактична:
- Формування умінь учнів розв'язувати показникові рівняння і системи різними способами.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Повідомлення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх. Перевірка домашнього завдання.
Три учні відтворюють на відкидних дошках розв'язування вправ:
1 учень — № 34 із «Запитань для повторення»;
2 учень — № 1 (12—14);
3 учень — № 1 (15, 16).
У цей час учні виконують завдання № 1 (19, 21, 47).
II. Набуття умінь розв'язувати системи показникових рівнянь.
Початковий рівень
1. Які з пар (1; 0); (0; 1) є розв'язками системи рівнянь:
а) 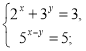 б)
б) 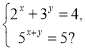
Відповідь: а) (1; 0); б) (0; 1).
Середній рівень
1. Розв'яжіть системи рівнянь: а) ![]() б)
б) ![]()
Відповідь: а) (1; 1); б) (2; 0).
2. Розв'яжіть системи рівнянь: а) 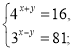 б)
б) 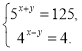
Відповідь: а) (3; -1); б) (2; 1).
Достатній рівень
1. Розв'яжіть системи рівнянь: а)  б)
б) 
Відповідь: а) (1; 2), (2; 1); б) (1; 2), (2; 1).
2. Розв'яжіть системи рівнянь: а) 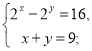 б)
б) 
Відповідь: а) (5; 4); б) (3; 0).
Високий рівень
1. Розв'яжіть системи рівнянь: а)  б)
б) 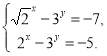
Відповідь: а) (4; 1); б) (2; 2).
2. Розв'яжіть системи рівнянь: а) 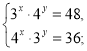 б)
б) 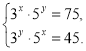
Відповідь: а) (1; 2); б) (1; 2).
II. Сприймання і усвідомлення матеріалу.
При розв'язуванні систем показникових рівнянь використовуються звичні прийоми розв'язування показникових рівнянь і знайомі вам прийоми розв'язування систем рівнянь.
Розглянемо приклади.
Приклад 1. Розв'яжіть систему рівнянь 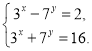
Розв'язання
Зробимо заміну 3х = а, 7у = b, тоді матимемо систему; ![]()
Розв'яжемо її: ![]()
![]()
![]()
Отже, 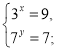
![]()
Відповідь: (2; 1).
Приклад 2. Розв'яжіть систему рівнянь 
Розв'язання


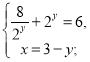
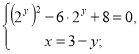
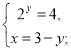 або
або 
![]() або
або ![]()
Отже, ![]() і
і ![]() є розв'язками системи.
є розв'язками системи.
Відповідь: (1; 2), (2; 1).
Приклад 3. Розв'яжіть систему рівнянь 
Розв'язання
Перемножимо і розділимо рівняння системи, тоді одержимо:
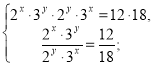

![]()
![]()
![]()
Відповідь: (2; 1).
ІІІ. Підсумок уроку.
ІV. Домашнє завдання.
Розділ ІV § 2 № 1 (25, 28, 30, 46).
ТЕМА УРОКУ
Логарифм числа. Основні властивості логарифмів. Основна логарифмічна тотожність.
МЕТА УРОКУ
Дидактична:
- Формування поняття логарифма числа. Познайомити учнів з основною логарифмічною тотожністю.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Повідомлення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
 II. Сприймання і усвідомлення поняття логарифма числа, основної логарифмічної тотожності.
II. Сприймання і усвідомлення поняття логарифма числа, основної логарифмічної тотожності.
Рівняння ах = b, де a > 0, а ≠ 1, b > 0 (рис. 162) має єдиний корінь. Цей корінь називається логарифмом числа b за основою a і позначається logab.
Наприклад: коренем рівняння 2х = 8 є число 3, тобто log2 8 = – 3.
!
Логарифмом додатного числа b за основою а, де а > 0, а ≠ 1, називається показник степеня, до якого треба піднести число а, щоб одержати число b.
Наприклад: log28 = 3, оскільки 23 = 8;
log2 ![]() = – 2, оскільки 2-2 =
= – 2, оскільки 2-2 = ![]() ;
;
log7l = 0, оскільки 70 = 1.
Десятковими логарифмами називаються логарифми за основою 10, позначаються lg.
Наприклад, lg100 = 2, lg0,0001 = - 4.
Натуральними логарифмами називаються логарифми за основою е (число е — ірраціональне, е == 2,718281828459045...), позначаються ln.
Наприклад: ln е = 1, ln е2 = 2, ln ![]() = -1.
= -1.
Означення логарифма можна коротко записати так: ![]() .
.
Ця рівність справедлива при b > 0, a > 0, a ≠ 1 називається основною логарифмічною тотожністю.
Наприклад: ![]() ,
,  .
.
При виконанні перетворень виразів, які містять логарифми, при обчисленнях і при розв'язуванні рівнянь, нерівностей часто використовуються властивості логарифмів.
Для будь-яких а > 0, а ≠ 1 і будь-яких додатних х і у виконуються рівності:
|
l. logа l = 0; 2. logаa = 1; 3. logа xy = logа x + logа y;
4. logа
5. logа х р = p logа x (р
6.
7. loga x = |
Доведемо рівності 3—7. За основною логарифмічною тотожністю
![]() (І)
(І)
![]() (II)
(II)
Перемноживши рівності (І) і (II), одержуємо:
ху = ![]() ·
· ![]() =
= ![]() ,
,
звідси за означенням логарифма маємо
loga xy = loga x + loga y.
Отже, логарифм добутку дорівнює сумі логарифмів.
Розділивши рівності (І) і (II), одержуємо: ![]() =
= ![]() ,
,
звідси за означенням логарифма маємо: loga ![]() = loga х – loga у.
= loga х – loga у.
Отже, логарифм частки дорівнює різниці логарифмів.
Піднісши ліву і праву частини рівності (І) до степеня з показником р, маємо: ![]() (ІІІ)
(ІІІ)
звідси за означенням логарифма маємо: logа х р = p logа x.
Отже, логарифм степеня дорівнює добутку показника степеня на логарифм основи цього степеня.
З рівності (III) маємо: ![]() , звідси за означенням логарифма маємо:
, звідси за означенням логарифма маємо:
![]() , тоді p
, тоді p![]() ;
;  .
.
Формула 7 називається формулою переходу від одної основи логарифма до другої основи. Доведемо її.
За правилом логарифмування степеня (формула 5) та основною логарифмічною тотожністю одержуємо:
![]() ,
,
звідси logb х = loga х · logb a
або loga = ![]() .
.
За допомогою формули 7 можна знаходити логарифми з довільною основою а, маючи таблиці логарифмів, складених для якої-небудь основи b. Найбільш вживаними є таблиці десяткових і натуральних логарифмів.
Дія знаходження логарифма числа (виразу) називається логарифмуванням.
Приклад. Прологарифмуйте вираз у = ![]() .
.
Розв'язання
lg y = lg ![]() = lg (a2b2) – lg c3 = lg a2 + lg b2 – lg c3 = 2 lga + 2 lg b – 3 lg c.
= lg (a2b2) – lg c3 = lg a2 + lg b2 – lg c3 = 2 lga + 2 lg b – 3 lg c.
Дія, обернена до логарифмування, називається потенціюванням.
!
Потенціювання — знаходження числа (виразу) за його логарифмом.
Приклад. Пропотенціюйте вираз lg х = ![]() lg 5а – 3 lg b + 4 lg c.
lg 5а – 3 lg b + 4 lg c.
Розв'язання
lg x = ![]() lg 5a – 3 lg b + 4 lg c; lg x = lg
lg 5a – 3 lg b + 4 lg c; lg x = lg ![]() – lg b3 + lg c4;
– lg b3 + lg c4;
lg x = lg ![]() – lg b3 + lg c4; lg x = lg (
– lg b3 + lg c4; lg x = lg (![]() · с4) – lg b3;
· с4) – lg b3;
lg x = lg ![]() ; x =
; x = ![]() .
.
III. Осмислення поняття логарифма та основної логарифмічної тотожності.
1. Розглянемо приклади використання формул 3-7. Обчислимо:
1) log6 18 + log6 2 = log6(18 – 2) = log6 36 = 2;
2) log12 48 – log12 4 = log6 ![]() = log12 12 = 1;
= log12 12 = 1;
3) log6 ![]() = log6
= log6 ![]() =
= ![]() log6 3 =
log6 3 = ![]() · 1 =
· 1 = ![]() ;
;
4) log125 5 = log125 5 = ![]() log5 5 =
log5 5 = ![]() · 1 =
· 1 = ![]() ;
;
5) ![]() = log4 16 = log4 42 = 2 log4 4 = 2 · 1 = 2.
= log4 16 = log4 42 = 2 log4 4 = 2 · 1 = 2.
IV. Підведення підсумків уроку.
V. Домашнє завдання.
Розділ V § 1 (1, 2). Запитання і завдання для повторення до розділу V № 1—5. Вправи № 2, 4, 6, 18.
ТЕМА УРОКУ
Логарифмічна функція, її графік і властивості
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з логарифмічною функцією, її властивостями і графіком.
Розвиваюча:
- розвивати аналітичне мислення;
- розвивати вміння узагальнювати та систематизувати вивчений матеріал.
ТИП УРОКУ
Засвоєння нових знань і вмінь.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань. Вивчення нового матеріалу.
- Повідомлення нового матеріалу.
- Засвоєння нових знань і вмінь.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх. Перевірка домашнього завдання.
1. Три учні відтворюють розв'язування вправ № 13, 15, 20.
2. Розв'язування вправ, аналогічних домашнім.
а) Обчисліть: ![]() ;
; ![]() .
.
Розв'язання
![]() =
= =
=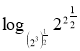 =
= =
= =
=![]() ·
·![]() =
=![]() .
.
![]() =
= ==
==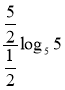 =
=![]() ·
·![]() = 5.
= 5.
б) Обчисліть ![]() .
.
Розв'язання
![]() =
=![]() =
=![]() =
=![]() = 52 · 3-2 =
= 52 · 3-2 =
= 25 · ![]() =
= ![]() =
= ![]() .
.
II. Аналіз самостійної роботи, проведеної на попередньому уроці.
III. Засвоєння властивостей логарифмічної функції та її графіка.
!
Функція виду у = loga x, де а — задане число, а > 0, а ≠ 1 називається логарифмічною функцією.
Логарифмічна функція має такі властивості:
- Область визначення функції — множина всіх додатних чисел. Ця властивість випливає із означення логарифма, оскільки вираз loga х має смисл тільки при х > 0.
- Область значень логарифмічної функції — множина R усіх дійсних чисел. Ця властивість випливає з того, що для будь-якого дійсного числа b є таке додатне число х, що loga x = b, тобто рівняння loga x = b має єдиний корінь. Такий корінь існує і дорівнює х = аb, оскільки loga аb = b.
- Логарифмічна функція на всій області визначення зростає (при а > 1) або спадає (при 0 < а < 1). Нехай а > 1. Доведемо, що якщо x2 > х1 > 0, то
loga х2 > loga x1. Користуючись основною логарифмічною тотожністю, умовою x2 > х1, можна записати ![]() . З останньої нерівності за властивістю степеня з основою а > 1 маємо, що loga х2 > loga x1.
. З останньої нерівності за властивістю степеня з основою а > 1 маємо, що loga х2 > loga x1.
Нехай 0 < а < 1. Доведемо, що якщо x2 > х1 > 0, то loga х2 < loga x1. Записавши умову x2 > х1 у вигляді ![]() одержуємо loga х2 < loga x1, оскільки 0 < а < 1.
одержуємо loga х2 < loga x1, оскільки 0 < а < 1.
- Якщо а > 1, то функція у = loga x приймає додатні значення при х > 1, від'ємні — при 0 < х < 1. Якщо 0 < а < 1, то функція у = loga x приймає додатні значення при 0 < х < 1, від'ємні — при х > 1.
 Рис. 163
Рис. 163 
Ця властивість випливає з того, що функція у = loga x приймає значення, рівне нулю, при х = 1 і є зростаючою на проміжку х > 0, якщо а > 1, і спадною, якщо 0 < а < 1. Спираючись на доведені властивості, неважко побудувати графік функції у = loga x (рис. 163).
Графіки показникової функції і логарифмічної функції, які мають однакові основи, симетричні відносно прямої у = х (рис. 164), бо функції у = 0х і у = loga x є взаємно оберненими.
IV. Осмислення властивостей логарифмічної функції.
1. Усне виконання вправ № 37—39, 40.
2. Письмове виконання вправ № 46, 50.
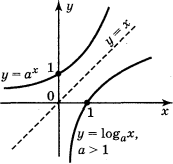 Рис. 164
Рис. 164 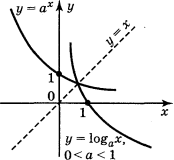
V. Систематизація вивченого матеріалу.
Повторення властивостей логарифмічної функції і заповнення таблиці 23.
Таблиця 23
Логарифмічна функція |
||||
|
|
1. D(y) = .... 2. Е(у) = .... |
|
||
|
a > 1 3. Якщо х1 < x2 то ………………….. 4. loga x > 0, якщо ..... loga х = 0, якщо ..... loga x < 0, якщо ..... |
|
0 < а < 1 3. Якщо х1 < x2 то ………………….. 4. loga x > 0, якщо ..... loga х = 0, якщо ..... loga x < 0, якщо ..... |
||
VI. Підведення підсумків уроку.
VII.Домашнє завдання.
Розділ V § 2. Запитання і завдання для повторення до розділу V № 15—25. Вправи № 44, 49.
ТЕМА УРОКУ
Логарифмічні рівняння
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «логарифмічні рівняння» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Декілька студентів біля дошки показують приклади розв’язання домашнього завдання.
Фронтальне опитування:
- Що називається логарифмом?
Логарифмом числа N за основою а (a>0, a1) називається показник степеня х, до якого треба піднести основу а, щоб отримати числоN(N>0).
-
Якщо
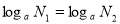 , то що ми можемо сказати за числа від яких беруться логарифми?
, то що ми можемо сказати за числа від яких беруться логарифми?
Число ![]() .
.
- Назвіть властивості логарифма?
- Що називається потенціюванням?
Перетворення за допомогою якого за даним логарифмом числа (виразу), визначають саме число (вираз), називають потенціюванням.
- Що значить про логарифмувати вираз?
Плологарифмувати одночлен означає виразити його логарифм через логарифми додатних чисел, що входять до його складу.
ІІІ.
Логарифмічними називаються рівняння, які містять змінну під знаком логарифма.
![]() (а>0, a1)
(а>0, a1)
Особливістю розв’язання логарифмічних рівнянь є необхідність знаходження ОДЗ рівняння або перевірка отриманих значень невідомих, в зв’язку з тим, що логарифми існують тільки від додатних чисел і основа повинна бути додатною.
Способи розв’язання:
- Логарифмічні рівняння, які розв’язуються за означенням.
Наприклад,
1) ![]() 2)
2) ![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]() ОДЗ:
ОДЗ: ![]()
Відповідь: ![]() Відповідь:
Відповідь: ![]()
- Логарифмічні рівняння, які розв’язуються потенціюванням.
Наприклад,
3) ![]()
![]()
![]()
ОДЗ: ![]()
Відповідь: ![]() .
.
4) ![]()
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Перевірка: ![]()
![]()
![]()
![]()
4=4 4=4
Відповідь: 14; 6.
- Логарифмічні рівняння, які розв’язуються методом підстановки.
Наприклад,
5) ![]()
![]() ;
; ![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь:100; 1000.
- Логарифмічні рівняння, в яких змінна знаходиться в основі і в показнику степеня розв’язуються логарифмуванням.
Наприклад,
6) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь:100; 0,01.
- Логарифмічні рівняння, до яких входять логарифми за різними основами розв’язуються зведенням до однієї основи.
Наприклад,
7) ![]()
![]()
![]()
![]()
![]() ;
; ![]() ;
; ![]()
ОДЗ: ![]()
Відповідь: 64.
ІV. Розв’язати рівняння:
№ 52
5) ![]()
![]()
![]() ;
; ![]() ;
; ![]()
Перевірка: ![]()
0=0 0=0
Відповідь: 0; 1.
4) ![]()
![]()
Перевірка: ![]() логарифми не існують
логарифми не існують
Відповідь: розв’язку не має .
10) ![]()
![]() ;
; ![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь: ![]() .
.
12) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь:10; 0,0001.
13) ![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь: ![]() .
.
№ 54
3) ![]()
![]() ;
; ![]() ;
; ![]()
![]()
![]()
![]()
![]()
ОДЗ: ![]()
Відповідь:100; ![]() .
.
V. Домашнє завдання:
Вивчити конспект. № 52(8,2,14), №53(12,10) Шкіль стр. 240.
ТЕМА УРОКУ
Логарифмічні рівняння. Системи логарифмічних рівнянь
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «логарифмічні рівняння та їх системи» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Математичний диктант.
|
І варіант |
ІІ варіант |
|
1. Означення логарифма |
1. Означення логарифмічного рівняння |
|
2. Основна логарифмічна тотожність |
2. Логарифм частки (2 властивість) |
|
3. Логарифм добутку (1 властивість) |
3. |
|
4. |
4. Перехід до іншої основи (6 властивість) |
|
5.Що таке потенціювання |
5. Що значить про логарифмувати вираз |
|
6. |
6. |
1. Розв’язати рівняння:
1) ![]()
III. Розв'язування систем логарифмічних рівнянь.
При розв'язуванні систем логарифмічних рівнянь використовують ті саме способи, що й при розв'язуванні алгебраїчних систем. Розглянемо приклади.
Приклад 1. Розв'яжіть систему рівнянь: ![]()
Розв'язання
Додамо і віднімемо почленно рівняння системи, тоді одержимо:
![]()
![]()
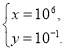
Відповідь: (106; 10-1).
Приклад 2. Розв'яжіть систему рівнянь 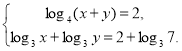
Розв'язання

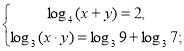

![]()
![]()
![]()
![]()

Тоді маємо  або
або  .
.
Перевіркою впевнюємося, що (9; 7), (7; 9) — розв'язки системи.
Відповідь: (9; 7), (7; 9).
IV. Формування умінь розв'язувати системи логарифмічних рівнянь.
Розв'язування вправ № 55 (3; 4), 56 (2; 4), 57 (2).
V. Підведення підсумків уроку.
VI. Домашнє завдання.
Розділ V § 3. Запитання і завдання для повторення розділу V № 32.
Вправи № 55 (1; 2), 56 (1, 3). Повторити властивості логарифмічної функції.
ТЕМА УРОКУ
Логарифмічні нерівності
МЕТА УРОКУ
Дидактична:
- Формування умінь учнів розв'язувати логарифмічні нерівності.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
1. Два учня відтворюють розв'язання вправ № 55 (2), 56 (3).
2. Колективне розв'язування вправ № 57 (1; 3).
III. Сприймання і усвідомлення розв'язування найпростіших логарифмічних нерівностей.
Як відомо, логарифмічна функція у = logа х зростає при a > 1, спадає — при 0 < a < 1. Із зростання функції у = logа x у першому випадку і спадання — у другому випадку випливає:
1) При a > 1 нерівність logа х2 > logа х1 рівносильна системі 
2) При 0 < a < 1 нерівність logа х2 > logа х1 рівносильна системі 
Розглянемо приклади.
Приклад 1. Розв'яжіть нерівність log2 x < 3.
 Розв'язання
Розв'язання
Оскільки 3 = log223 = log28, то запишемо дану нерівність у вигляді log2 x < log28. Оскільки функція
у = log2x зростаюча при х > 0, то маємо: ![]() отже, 0 < х < 8 (рис. 166). Відповідь: х
отже, 0 < х < 8 (рис. 166). Відповідь: х ![]() (0; 8).
(0; 8).
Приклад 2. Розв'яжіть нерівність ![]() .
.
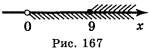 Розв'язання
Розв'язання
Запишемо дану нерівність у вигляді:
![]() . Оскільки функція у =
. Оскільки функція у = ![]() х спадна при х > 0, маємо:
х спадна при х > 0, маємо: ![]() отже, х
отже, х ![]() 9 (рис. 167).
9 (рис. 167).
Відповідь: х ![]() [9; +
[9; + ![]() ).
).
Як правило, логарифмічна нерівність зводиться до нерівностей виду: logaf(x) > logag(x), де а > 0, а ≠ 1.
Якщо а > 1, то нерівність logaf(x) > logag(x) рівносильна системі нерівностей: 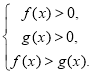
Якщо 0 < а < 1, то нерівність logaf(x) > logag(x) рівносильна системі нерівностей: 
Приклад 3. Розв'яжіть нерівність: ![]() .
.
Розв'язання
Так як - 1 = log0,50,5-1 = log0,52, то log0,5(x2 + х) > log0,52.
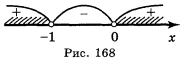 Одержана нерівність рівносильна системі
Одержана нерівність рівносильна системі

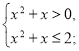
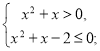
![]()
Розв'язком першої нерівності (рис. 168)
є (-![]() ; -1)
; -1)![]() (0; +
(0; +![]() ).
).
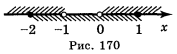 Розв'язком другої нерівності (рис. 169) є [-2; 1].
Розв'язком другої нерівності (рис. 169) є [-2; 1].
Тоді маємо (рис. 170) x ![]() [-2;-l)
[-2;-l)![]() (0;l].
(0;l].
Відповідь: [-2; -1)![]() (0; 1].
(0; 1].
IV. формування умінь розв'язувати логарифмічні нерівності.
Приклад 1. Розв'яжіть нерівність log![]() х – log5 x > 2.
х – log5 x > 2.
Розв'язання
Нехай log5х = у, тоді отримаємо нерівність у2 – у – 2 > 0.
Розв'яжемо отриману нерівність методом інтервалів (рис. 171):
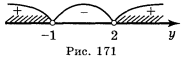 y
y ![]() (-
(-![]() ; -l)
; -l)![]() (2; +
(2; +![]() ).
).
Враховуючи заміну матимемо:
-
log5 x < -1; log5 x < log5
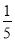 ;
; 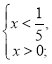 х
х 
 ;
;
-
log5 x > 2; log5 x > log525;
 x
x  (25; +
(25; +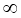 ). Отже,
). Отже, 
 (25; +
(25; +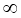 ) –
) –
розв'язок даної нерівності.
Відповідь: ![]()
![]() (25; +
(25; +![]() ).
).
 Приклад 2. Розв'яжіть нерівність
Приклад 2. Розв'яжіть нерівність ![]() .
.
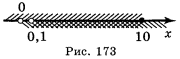 Розв'язання
Розв'язання
Нехай lg x = у, тоді матимемо нерівність
![]() ; у ≠ 1;
; у ≠ 1; ![]() ;
; ![]() ;
; ![]() .
.
Розв'яжемо отриману нерівність методом інтервалів (рис. 172): у ![]() (-1; 1].
(-1; 1].
Враховуючи заміну, отримаємо -1 < lg x ![]() 1.
1.
Тоді ![]()
![]()
 отже, х
отже, х ![]() (0,1; 10] (рис. 173).
(0,1; 10] (рис. 173).
Відповідь: (0,1; 10].
Приклад 2. Розв'яжіть нерівність log x-3(х – 1) < 2.
Розв'язання
Нехай у = log x-3(х – 1) – 2 і у < 0. Область визначення функції знаходимо із системи: 
 х
х ![]() (3; 4)
(3; 4) ![]() (4; +
(4; +![]() ).
).
Знайдемо нулі функції: log x-3(х – 1) = 2; х – 1 = (х – 3)2; х – 1 = х2 – 6х + 9; х2 – 7х + 10 = 0; х = 5, х = 2. х = 2 — не входить в область визначення функції. Перевіркою переконуємося, що х = 5 — нуль функції.
Розіб'ємо область визначення функції на проміжки точкою 5 та знайдемо знаки функції на утворених проміжках (рис. 175).
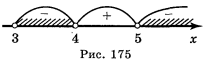 Отже, х
Отже, х ![]() (3; 4)
(3; 4) ![]() (5; +
(5; +![]() ).
).
Відповідь: (3; 4) ![]() (5; +
(5; +![]() ).
).
V. Підведення підсумків уроку.
VI. Домашнє завдання.
Розділ V § 3. Запитання і завдання для повторення розділу V № 33—34. Вправа № 58 (1; 4; 5; 6; 9).
ТЕМА УРОКУ
Тригонометричні функції кута. Радіанна система вимірювання кутів і дуг
МЕТА УРОКУ
Дидактична:
- Повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута.
Розвиваюча:
- розвивати аналітичне мислення;
ТИП УРОКУ
Урок узагальнення та систематизації знань.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. 1. Побудуйте графіки функцій (індивідуальні картки):
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Відповідь: а) рис. 25; б) рис. 26; в) рис. 27; г) рис. 28.



2. Побудуйте графіки функцій (індивідуальні картки):
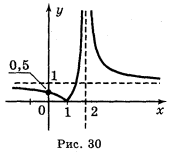
 а)
а) ![]() ; б)
; б) ![]()
Відповідь: а) рис. 29; б) рис. 30.
Повторення відомостей про тригонометричні функції гострих кутів прямокутного трикутника.
Провести повторення шляхом фронтальної бесіди з використанням таблиці 3.

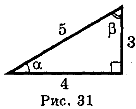 1. Дайте означення синуса гострого кута прямокутного трикутника.
1. Дайте означення синуса гострого кута прямокутного трикутника.
2. Дайте означення косинуса гострого кута прямокутного трикутника.
3. Дайте означення тангенса гострого кута прямокутного трикутника. (Увести поняття котангенса гострого кута прямокутного трикутника).
 4. Користуючись рис. 31, знайдіть sin α, cos α, tg α, ctg α, sin β, cos β, tg β, ctg β.
4. Користуючись рис. 31, знайдіть sin α, cos α, tg α, ctg α, sin β, cos β, tg β, ctg β.
5. Обчисліть:
а) 2 cos 60° + ![]() cos 30°; б) 3tg45°·tg60° ;
cos 30°; б) 3tg45°·tg60° ;
в) 2 cos 30° + 6 cos 60° – 4 tg 45°; г) 2 ctg 60° – 2 sin 60° .
6. Спростіть:
a) (l – cosα)(l + cosα); 6) tgα – ctgα + sin2 α + cos2 α.
III. Повторення відомостей про тригонометричні функції довільного кута.
 У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола. Нагадаємо ці означення. Нехай дано коло радіуса R, центр якого знаходиться у початку координат. Відкладемо від додатної півосі у верхню півплощину кут α, друга сторона якого перетне коло в точці Рα(х; у) (рис. 32).
У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола. Нагадаємо ці означення. Нехай дано коло радіуса R, центр якого знаходиться у початку координат. Відкладемо від додатної півосі у верхню півплощину кут α, друга сторона якого перетне коло в точці Рα(х; у) (рис. 32).
Синусом кута називається відношення ординати точки Рα(х; у) кола до його радіуса: ![]() .
.
Косинусом кута називається відношення абсциси точки Рα(.х; у) кола до його радіуса: ![]() .
.
Тангенсом кута називається відношення ординати точки Рα(х; у) до її абсциси:![]() .
.
Котангенсом кута називається відношення абсциси точки Рα(х; у) до її ординати: ![]() .
.
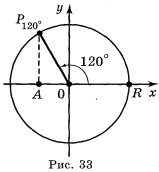 Приклад 1. Знайти sin α, cos α, tg α, ctg α, якщо α = 120°. Побудувавши точку Р120º, маємо (рис. 33):
Приклад 1. Знайти sin α, cos α, tg α, ctg α, якщо α = 120°. Побудувавши точку Р120º, маємо (рис. 33):
![]()
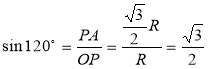 ;
;  ;
;  ;
;  ;
;
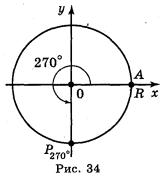 Якщо будь-який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному — проти годинникової стрілки, від'ємному — за годинниковою стрілкою), то дане визначення можна використовувати для будь-яких кутів.
Якщо будь-який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному — проти годинникової стрілки, від'ємному — за годинниковою стрілкою), то дане визначення можна використовувати для будь-яких кутів.
Приклад 2. Знайти sin α, cos α, tg α, ctg α, якщо α = 270°. При повороті на 270° навколо точки О радіус ОА, який дорівнює R, перейде в радіус ОР, тоді (рис. 34)
Р270º·(0; -R ) і, отже, sin 270° = ![]() = -1, cos 270° =
= -1, cos 270° = ![]() = 0, ctg270° =
= 0, ctg270° = ![]() = 0 , tg 270° не має змісту.
= 0 , tg 270° не має змісту.
Із курсу геометрії відомо, що величина кута в градусах виражається числом від 0° до 180''. Кут Повороту може виражатися в градусах, яким завгодно дійсним числом від -![]() до +
до +![]() .
.
Приклад 3. Якщо початковий радіус ОА зробив повний оберт проти годинникової стрілки, то кут повороту буде дорівнювати 360° (рис. 35). Якщо початковий радіус ОА зробив півтора оберти проти годинникової стрілки, то кут повороту буде дорівнювати 540º (рис. 36). Якщо початковий радіус ОА зробив два повних оберти і чверть оберту за годинниковою стрілкою, то кут повороту буде дорівнювати 2 (-360°) - 90° = - 810° (рис. 37).



 Розглянемо радіуси ОА і ОВ. Існує безліч кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ (рис. 38). Нехай <AОВ = α, тоді відповідні кути повороту будуть дорівнювати α + 360°n, де n — ціле число (п
Розглянемо радіуси ОА і ОВ. Існує безліч кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ (рис. 38). Нехай <AОВ = α, тоді відповідні кути повороту будуть дорівнювати α + 360°n, де n — ціле число (п ![]() Ζ).
Ζ).
Якщо початковий радіус переходить у радіус ОВ при повороті на кут а, то в залежності від того, у якій четверті буде радіус 0B, кут α називають кутом цієї чверті. Так, якщо 0° < α < 90°, то α – кут І чверті; якщо 90° < α < 180°, то α — кут II чверті; якщо 180° < α < 270°, то α — кут III чверті; якщо 270° < α < 360°, то α — кут IV чверті. Кути 0°; ±90°; ±180°; ±270°; ±360° не відносяться ні до якої чверті.
У курсі геометрії було доведено, що значення синуса, косинуса і тангенса кута α, де 0° < α < 180° залежить тільки від α і не залежить від довжини R. І в загальному вигляді sin α, cos α, tg α, а також ctg α залежать тільки від кута α.
Вирази sin α і cos α, визначені для будь-яких а, так само як для будь-якого кута повороту, можна знайти відношенням ![]() і
і ![]() .
.
Вираз tg α має смисл при будь-яких а, крім кутів повороту ±90°; ±270°; ±450°, тобто α ![]() 90°+180° n , (п
90°+180° n , (п ![]() Ζ).
Ζ).
Вираз ctg α має смисл при будь-яких а, крім кутів повороту 0°; ±180°; ±360°.., тобто, α ![]() 180° n , (п
180° n , (п ![]() Ζ).
Ζ).
Кожному допустимому значенню α відповідає єдине значення sin α, cos α, tg α, ctg α, тому синус, косинус, тангенс, котангенс є функціями кута α. Їх називають тригонометричними функціями.
Виконання вправ
- Чому дорівнюють кути повороту, які показано на рисунку 39.



Рис. 39
2. Накресліть коло із центром у початку координат і побудуйте кут повороту, що дорівнює: а) 135°; б) -120°; в) 540°; г) -810°.
3. Запишіть всі кути поворотів, при яких радіус ОА переходить у радіус ОВ (рис. 40).
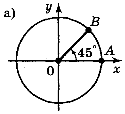



Рис. 40
4. Побудуйте коло з центром у початку координат і кути повороту, що дорівнюють:
а) 90° + 360° n, (п ![]() Z); б) 180° + 360° n, (п
Z); б) 180° + 360° n, (п ![]() Z);
Z);
в) –90º + 180° n, (п ![]() Z); г) ±60° + 360º n, (п
Z); г) ±60° + 360º n, (п ![]() Z).
Z).
5. Визначте, кутом якої чверті є кут α, якщо кут а дорівнює:
а) 181°; б) 179°; в) 271°; г) 361°; д) 345°; є) 800°.
6. Серед кутів повороту 790°; 500°; -30°; 1580°; -220°; -290° знайдіть такі, при яких початковий радіус займе таке саме положення, як і при повороті на кут: а) α = 70°; 6) α = 140°.
7. Накресліть коло з центром на початку координат і радіусом R = 5 см. Поверніть початковий радіус на кут α і знайдіть наближене значення sin α, cos α, tg α, ctg α, якщо α = 50°; 175°; -100°.
IV. Підсумок уроку.
V. Домашнє завдання.
Розділ І § 2. Запитання і завдання для повторення № 32-34. Вправи № 4, 5.
ТЕМА УРОКУ
Періодичність тригонометричних функцій
МЕТА УРОКУ
Дидактична:
- Введення поняття періодичної функції; знаходження найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій у = sin (kx + b), у = cos (kx + b), у=tg(kx+b), у = ctg (kx + b).
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
Проведення самостійної роботи
І в. II в.
1. Побудуйте на одиничному колі точку Рα, на яку відображаються початкова точка Р0 (1; 0) при повороті на α рад навколо центра, якщо:
|
|
|
|
2. Знайдіть
|
2. Знайдіть
|
|
3. Визначте знак добутку sin 1 · cos 2 · tg 3. (5 бали) |
3. Визначте знак добутку сos 1 · sin 2 · ctg 3. (5 бали) |
Відповідь:


І в.: 1. Рис. 55. 2. 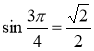 ,
,  ,
, ![]() ,
, ![]() . 3. Плюс.
. 3. Плюс.
ІІ в.: 1. Рис. 56. 2.  ,
, ![]() ,
, ![]() ,
,  .3.мінус.
.3.мінус.
II. Формування поняття періодичної функції, періодe функції.
У природі часто зустрічаються явища, які повторюються періодично. Наприклад, Земля при обертанні навколо Сонця періодично повертається У своє початкове положення через рік, два роки, три роки і т. д., тому говорять, що період обертання Земля навколо Сонця дорівнює одному року. Періодичний характер мають рухи маховика і колінчатого вала. Властивість періодичності мають звукові, електромагнітні явища, робота серця людина і т. д. Закономірності періодичних явищ описуються періодичними функціями, до вивчення яких ми і приступаємо.
!
Функція у = f(x) називається періодичною з періодом Т ![]() 0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) = f(x – Т) = f(x).
0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) = f(x – Т) = f(x).
Так як одній і тій самій точці Рα одиночного кола відповідає нескінченна множина дійсних чисел α + 2πk, де k ![]() Z, то
Z, то
sin(α + 2nk) = sin α
cos(α + 2nk) = cos α
Звідси випливає, що 2nk – періоди функції синус і косинус (k ![]() 0).
0).
Доведемо, що число 2π є найменшим додатним періодом функції у = cos х. Нехай Τ > 0 – період косинуса, тобто для будь-якого х виконується нерівність cos (х + Τ) = cos x. Взявши х = 0, одержимо cos Т = 1. Звідси Τ = 2nk, k ![]() Ζ. Через те що Τ > 0, Τ може дорівнювати 2π, 4π, 6π... і тому період не може бути меншим 2π.
Ζ. Через те що Τ > 0, Τ може дорівнювати 2π, 4π, 6π... і тому період не може бути меншим 2π.
Можна довести, що найменший період функції у = sin x теж дорівнює 2π. Нехай Τ — довільний період синуса. Тоді sin(x + Τ) = sin x для будь-якого х. Взявши х = ![]() , одержимо sin
, одержимо sin  = sin
= sin ![]() = 1, але sin
= 1, але sin  = 1, якщо Т +
= 1, якщо Т + ![]() =
= ![]() + 2πn , n
+ 2πn , n ![]() Ζ, тому Τ = 2πn. Найменше додатне число виду 2πn, n
Ζ, тому Τ = 2πn. Найменше додатне число виду 2πn, n![]() Ζ є число 2π.
Ζ є число 2π.
Доведемо, що найменшим додатним періодом функції у = tg х є число π. Нехай Т — додатний період тангенса, тобто tg(x+ Т) = tg х. Взявши х = 0, маємо tg Т = tg 0 = 0. Звідси Т = πn, n ![]() Ζ. Через те що найменше ціле додатне n = 1, π — найменший період функції у = tg х. Найменшим додатним періодом котангенса теж є число π. Отже, tg (α + πn) = tg α , ctg (α + πn) = ctg α.
Ζ. Через те що найменше ціле додатне n = 1, π — найменший період функції у = tg х. Найменшим додатним періодом котангенса теж є число π. Отже, tg (α + πn) = tg α , ctg (α + πn) = ctg α.
Як правило, слова “найменший додатний період” опускають. Прийнято говорити, що період тангенса і котангенса дорівнює π, а період косинуса і синуса дорівнює 2π.
Справедливе твердження.
!
Якщо функція у = f(x) періодична і має період Т, то функція у = Af(kx + b), де А, k, b — постійні (k ![]() 0), також періодична, причому її період дорівнює
0), також періодична, причому її період дорівнює ![]()
Доведемо це твердження.
Спочатку доведемо, що T0 = ![]() є періодом функції у = Af(kx + b):
є періодом функції у = Af(kx + b):
Af(k(x + T0) + b) = Af = Af(kx ± T + b) = Af(kx + b ± T) = Af(kx + b).
= Af(kx ± T + b) = Af(kx + b ± T) = Af(kx + b).
Нехай T0 — період функції у == Af(kx + b), тобто
Af(k(x + T0) + b)= Af(kx + b),
Af(kx +b+ kT0) = Af(kx +b).
Позначивши kx + b = x1, маємо Af(x + kT0) = Af(x1).
Через те що найменшим періодом функції f(x) є Т, то │k│T0 = Τ, звідси Т0 = ![]() .
.
III. Усвідомлення поняття періодичної функції.
Виконання вправ
1. Обчисліть: a) sin 1470°; б) tg 1860°; в) cos 1140°; r) ctg 1125°.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) 1.
; г) 1.
2. Знайдіть значення: a) sin ![]() ; б) cos
; б) cos ![]() ; в) tg
; в) tg ![]() ; г)ctg
; г)ctg![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) 1.
; г) 1.
3. Знайдіть найменший додатний період функцій:
а) у = ![]() sin2х; б) у = 3cos 4x; в) y = 5tg
sin2х; б) у = 3cos 4x; в) y = 5tg![]() ; г) y=0,6ctg
; г) y=0,6ctg![]() .
.
Відповідь: а) π; б) ![]() ; в)
; в) ![]() ; г) 4π.
; г) 4π.
4. Знайдіть значення sin α, якщо:
a) sin (α + 2π) = 0,3; б) sin (4π - α) = 0,2; в) sin (α + 6π) = 0,5; г) sin (α - 2π) = 0,1.
Відповідь: а) 0,3; б) -0,2; в) 0,5; г) 0,1.
V. Домашнє завдання.
Розділ І § 5. Запитання і завдання для повторення до розділу І № 47—49. Вправа № 24 (1—3). Повторіть геометричні перетворення графіків функцій (таблиця 1 підручника).
ТЕМА УРОКУ
Співвідношення між тригонометричними функціями одного аргументу
МЕТА УРОКУ
Дидактична:
- Вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значень тригонометричних функцій за однією відомою функцією. Ознайомити учнів з поняттям «логарифмічні рівняння та їх системи» та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
II. Мотивація навчання.
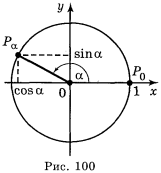 Дуже часто при розв'язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо задано лише значення однієї з них. Отже, на сьогоднішньому уроці ми повинні згадати формули (залежності), які пов'язують тригонометричні функції одного і того самого аргументу.
Дуже часто при розв'язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо задано лише значення однієї з них. Отже, на сьогоднішньому уроці ми повинні згадати формули (залежності), які пов'язують тригонометричні функції одного і того самого аргументу.
III. Сприймання і усвідомлення нового матеріалу.
1. Співвідношення між синусом і косинусом. Нехай точка Ρα(х, у) одиничного кола отримана поворотом точки Р0(1; 0) на кут α радіан, тоді згідно з означенням синуса і косинуса: х = cos α, у == sin α (рис. 100)
Оскільки точка Рα(х;у) належить одиничному колу, то координати (х; у) задовольняють рівнянню х2 + у2 = 1. Підставивши в це рівняння замість х і у значення cos α і sin α , отримаємо:
(cos α)2 + (sin α)2 = 1 або (враховуючи, що (cos α)2 = cos2 α, (sin α)2 = sin2 α)) cos2 α + sin2 α = 1.
Таким чином, sin2 α + cos2 α = l для всіх значень α. Ця рівність називається основною тригонометричною тотожністю.
З основної тригонометричної тотожності можна виразити sin α через cos α і навпаки. ![]() ,
, ![]() .
.
Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
a) cosα = ![]() і sinα =
і sinα = ![]() ; б) sinα = -
; б) sinα = -![]() і cosα = -
і cosα = -![]() ; в) sinα =
; в) sinα = ![]() і cosα = -
і cosα = - ![]() .
.
при одному і тому самому значенні α?
Відповідь: а) ні; б) так; в) так.
2. Знайдіть cos α, якщо sin α = 0,6 і ![]() < α < π.
< α < π.
Відповідь: cos α = -0,8.
3. Знайдіть sin α, якщо cos α = ![]() і
і ![]() < α < 2π.
< α < 2π.
Відповідь: sin α = -![]() .
.
4. Спростіть вирази:
а) 1 + sin2 α + cos2 α; б) 1 – sin2 α – cos2 α; в) 2sin2 α + cos2 α – 1;
г) (1 – cos α)(l + cos α); д) ![]() ; є) sin4 α – cos4 α + 1.
; є) sin4 α – cos4 α + 1.
Відповідь: а) 2; 6) 0; в) sin2 α; r) sin2 α; д) tg2α; є) 2sin2α.
5. Доведіть тотожності:
а) (1 – cos 2α)(l + cos 2α) = sin2 2α; 6) cos4 α – sin4 α = cos2 α – sin2 α;
в) (sin2 α – cos2 α)2 + 2cos2α sin2α = sin4 α + cos4 α;
r) 2cos2α sin2α + cos4α + sin4α = 1; д) sin6 α + cos6 α = 1 – 3sin2α cos2α;
є)  .
.
6. Знайдіть cos α, якщо cos4 α – sin4 α = ![]() .
.
Відповідь: cosα = ±![]() .
.
2. Співвідношення між тангенсом і котангенсом. Згідно з визначенням тангенса і котангенса,
![]() ,
, ![]() .
.
Перемноживши ці рівності, одержимо
![]()
Отже, tgα · ctgα = l для всіх значень α, крім α = ![]() , k, k
, k, k ![]() Ζ. із одержаної рівності можна виразити tg α через ctg α і навпаки:
Ζ. із одержаної рівності можна виразити tg α через ctg α і навпаки: ![]() ;
; ![]() .
.
Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
a) tg α = ![]() і ctgα =
і ctgα = ![]() ; б) tgα =
; б) tgα = ![]() і ctgα =
і ctgα = ![]() ; в) tg α = -
; в) tg α = - ![]() і ctg α = 2
і ctg α = 2
при одному і тому самому значенні α?
Відповідь: а) так; б) ні; в) ні.
2. Знайдіть
а) tg α, якщо ctg α = ![]() ; б) ctg α, якщо tg α = -1; в) tg α, якщо ctg α = 0.
; б) ctg α, якщо tg α = -1; в) tg α, якщо ctg α = 0.
Відповідь: а) ![]() ; б) -1; в) не існує.
; б) -1; в) не існує.
3. Дано: х = 2tg α, у = ctg α. Знайдіть ху.
Відповідь: ху = ![]() .
.
4. Дано tg α + сtg α = 2. Знайдіть tg 2 α + сtg2 α.
Відповідь: 2.
5. Спростіть:
а) tg α · сtg α – 1; б) sin2 α – tg α · сtg α; в) tg 1° · tg 3° · tg 5° · ... · tg 89°.
Відповідь: а) 0; б) – соs α; в) 1.
6. Доведіть тотожності:
а) (tg α + сtg α)2 - (tg α - сtg α)2 = 4; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
є) 4 + (сtg α - tg α)2 = (сtg α + tg α)2.
3. Співвідношення між тангенсом і косинусом, котангенсом і синусом.
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на соs2α, вважаючи, що соs2α ≠ 0, одержимо:
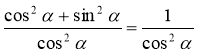 ;
; 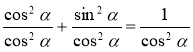 ,
,
звідси: ![]() , де
, де ![]() .
.
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на sіn2 α, вважаючи, що sіn α ≠ 0, одержимо
 ;
;  ,
,
звідси: ![]() , де
, де ![]() .
.
Виконання вправ______________________________
1. Чи можуть бути справедливими одночасно рівності.
а) tg α = ![]() і соs α =
і соs α = ![]() ; б) сtg α = 1 і sіn α =
; б) сtg α = 1 і sіn α = ![]() ; в) tg α =
; в) tg α = ![]() і sіn α =
і sіn α = ![]() при одному і тому ж значенні α?
при одному і тому ж значенні α?
Відповідь: а) ні; б) так; в) ні.
2. Відомо, що tg α = 2 і ![]() . Знайдіть sіn α, соs α і сtg α.
. Знайдіть sіn α, соs α і сtg α.
Відповідь: sіn α = ![]() ; соs α =
; соs α = ![]() ; сtg α =
; сtg α = ![]() .
.
3. Відомо, що sіn α = ![]() і 0 < α <
і 0 < α < ![]() . Знайдіть соs α, tg α, сtg α.
. Знайдіть соs α, tg α, сtg α.
Відповідь: соs α = ![]() ; tg α =
; tg α = ![]() ; сtg α =
; сtg α = ![]() .
.
4. Відомо, що сtg α = -3 і α — кут IV чверті. Знайдіть sіn α, соs α, tg α.
Відповідь: sіn α = ![]() ; соs α =
; соs α = ![]() ; tg α =
; tg α = ![]() .
.
5. Відомо, що соs α = ![]() і α — кут І чверті. Знайдіть sіn α, tg α, сtg α.
і α — кут І чверті. Знайдіть sіn α, tg α, сtg α.
Відповідь: sіn α = ![]() ; tg α =
; tg α = ![]() ; сtg α =
; сtg α = ![]() .
.
6. Спростіть вираз:
а)  ; б)
; б) 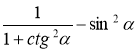 ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
Відповідь: а) 1; б) 0; в) 0; г) 0; д) ![]() ; є) tg α.
; є) tg α.
7. Доведіть тотожності:
а) ![]() ; б) (1 – сtg α)2 + (1 + сtg α)2 =
; б) (1 – сtg α)2 + (1 + сtg α)2 = ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
III. Підведення підсумків уроку.
IV. Домашнє завдання.
Розділ І § 8. Запитання і завдання для повторення до розділу І № 56-58. Вправи № 40 (1; 2; 4; 10), № 44 (1; 2).
ТЕМА УРОКУ
Формули додавання. Тригонометричні функції подвійного і половинного аргументу.
МЕТА УРОКУ
Дидактична:
- Вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
Розв'язання вправ, аналогічних до домашніх: вправа № 40 (11), 44 (3).
ІII. Сприймання і усвідомлення формул суми і різниці двох чисел.
 1. Розглянемо, як пов'язані косинус різниці двох чисел із синусом і косинусом цих самих чисел.
1. Розглянемо, як пов'язані косинус різниці двох чисел із синусом і косинусом цих самих чисел.
На одиничному колі позначимо точки Рα і Рβ (α > β) проведемо вектори ![]() і
і ![]() , тоді
, тоді ![]() (соs α; sіn α),
(соs α; sіn α),
![]() (соs β; sіn β) (рис. 101).
(соs β; sіn β) (рис. 101).
Знайдемо скалярний добуток векторів ![]() і
і ![]() , двома способами:
, двома способами:
1) ![]() ·
· ![]() = соs α · соs β + sіn α · sіn β;
= соs α · соs β + sіn α · sіn β;
2) ![]() ·
· ![]() =
= ![]() ·
·![]() · соs (α – β) = 1·1соs (α – β) = соs (α – β).
· соs (α – β) = 1·1соs (α – β) = соs (α – β).
Звідси маємо, що
соs (α – β) = соs α · соs β + sіn α · sіn β. (1)
Користуючись одержаною формулою, можна одержати інші формули:
соs (α + β) = соs α · соs β – sіn α · sіn β; (2)
sіn (α + β) = sіn α · соs β + соs α · sіn β; (3)
sіn (α – β) = sіn α · соs β – соs α · sіn β; (4)
 (5)
(5)
 (6)
(6)
Змінивши в формулі (1) β на –β і врахувавши, що соs(-β) = соs β, sіn(-β) = -sіnβ, одержимо
соs(α + β) = соs(α - (-β)) = соsα · соs(-β) + sіnα · sіn(-β) = соsα · соsβ – sіnα · sіnβ;
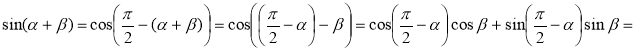 = sinα · cosβ + cosα · sinβ.
= sinα · cosβ + cosα · sinβ.
Таким чином,
sіn(α + β) = sіn α · соs β + соs α · sіn β
Змінивши в останній формулі β на – β одержимо:
sin(α - β) = sіn α · соs(-β) + соs α · sіn(-β)
Звідси sіn(α – β) = sіn α · соs β – соs α · sіn β
Виведемо формулу тангенса суми чисел:
 .
.
Отже 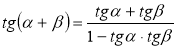
Змінивши β на – β, одержимо ![]()
1. Знайдіть значення виразів:
а) соs 42° соs 18° – sіn 42°sіn 18°; б) ![]() ;
;
в) sіn 56° соs 34° + соs 56° sіn 34°; г) ![]() ;
;
д)  ; є)
; є) 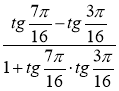 .
.
2. Спростіть вирази:
а) sіn(α + β) – sіn α · соs β; б) ![]() ;
;
в) 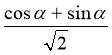 .
.
Відповідь: а) соs α · sіn β; б) sіn 2α;
в)  .
.
3. Обчисліть: а) соs 75°; б) tg 15°; в) сtg 75°; г) sіn ![]() ..
..
Відповідь: а) ![]() ; б) tg15° = tg (45° - 30°) = 2 -
; б) tg15° = tg (45° - 30°) = 2 - ![]() ; в) 2 -
; в) 2 - ![]() ; г)
; г) ![]() .
.
Сприймання і усвідомлення тригонометричних функцій подвійного аргументу.
Демонструється таблиця “Тригонометричні функції подвійного аргументу” (табл. 6).
Таблиця 6
Тригонометричні функції подвійного аргументуsіn 2α = 2sіn α соs α соз 2α = соs2 α - sіn2 α |
Виведемо формули, які виражають тригонометричні функції аргументу 2α через функції аргументу α.
Скористаємося формулою sіn(α + β) = sіn α · соs β + соs α · sіn β.
Вважаючи β = α, маємо:
sіn 2α = 2sіn α · соs α.
Аналогічно із формули соs(α + β) = соs α · соs β – sіn α · sіn β при α = β одержуємо:
соs 2α = соs2 α – sin2 α.
Із формули 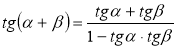 при β = α, маємо:
при β = α, маємо:  .
.
Виконання вправ
1. Обчисліть:
а) 2sin15° соs15°; б) соs215° – sіn215°; в)  ; г) (соs 75° – sіn 75°).
; г) (соs 75° – sіn 75°).
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Обчисліть sіn 2α, якщо а) sin α = ![]() ;
; ![]() < α < π; б) соs α =
< α < π; б) соs α = ![]() ; π < α <
; π < α < ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() .
.
3. Спростіть:
а) sіn α соs α; б) соs α · соs ![]() ; в) 2соs23α – 1;
; в) 2соs23α – 1;
г) 1 – 2sin2 5α; д) соs 4α + sіn2 2α; є) sіn 2α + (sin α – соs α)2.
Відповідь: а) ![]() sin2α; б)
sin2α; б) ![]() sіn2α; в) соs 6α; г) соs 10α; д) соs2α; є) 1.
sіn2α; в) соs 6α; г) соs 10α; д) соs2α; є) 1.
4. Доведіть тотожності:
а) 2соs2 α – соs 2α = 1; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
IV. Сприймання і усвідомлення тригонометричних функцій половинного аргументу.
За відомими значеннями тригонометричних функцій аргументу а можна знайти значення тригонометричних функцій аргументу ![]() якщо відомо, у якій чверті лежить кут α.
якщо відомо, у якій чверті лежить кут α.
Із формули соs 2x = соs2х - sіn2x при х = ![]() , одержуємо:
, одержуємо:
соs α = соs2 ![]() – sіn2
– sіn2 ![]() . (1)
. (1)
Запишемо основну тригонометричну тотожність у вигляді:
1 = соs2![]() + sin2
+ sin2![]() . (2)
. (2)
Складаючи почленно рівності (2) і (1) й віднімаючи почленно із рівності (2) рівність (1), одержуємо:
1+ соs α = 2соs2 ![]() ; (3)
; (3)
1 – соs α = 2sіn2 ![]() . (4)
. (4)
Формули (3) і (4) можна записати так:
![]() (5)
(5)
![]() (6)
(6)
Формули (5) і (6) називають формулами синуса і косинуса половинного аргументу. Ці формули називають також формулами зниження степеня.
Виконання вправ
1. Знайдіть числові значення виразу:
а) 2соs2 ![]() – 1; б) 1 – 2sin2
– 1; б) 1 – 2sin2 ![]() ; в)
; в) ![]() + 2sіn215°; г) -
+ 2sіn215°; г) - ![]() + 2соs215°. Відповідь: а)
+ 2соs215°. Відповідь: а) ![]() ; б)
; б) ![]() ; в) 1; г) 1.
; в) 1; г) 1.
2. Нехай соs α = 0,6 і 0 < α < ![]() . Обчисліть: а) sin
. Обчисліть: а) sin ![]() ; б) соs
; б) соs ![]() ; в) tg
; в) tg ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Обчисліть: а) sіn 15°; б) соs 15°; в) tg 22°30'.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. Спростіть:
а) ![]() ; б)
; б) ![]() .
.
Відповідь: а) 2соs α; б) tg α.
5. Доведіть тотожності:
а)  ; б)
; б) ![]() ; в)
; в) ![]() .
.
Демонструється таблиця 7.
Таблиця 7
Формули перетворення суми у добуток
|

1. Спростіть вирази:
а) ![]() –
– ![]() ; б)
; б) ![]() –
– ![]() .
.
в) sіn α · ![]() ; г)
; г) ![]() +
+![]() .
.
Відповідь: а) ![]() sin β; б) sin 2α; в)
sin β; б) sin 2α; в) ![]() ; г)
; г) ![]() соs α.
соs α.
2. Обчисліть:
а) соs 22° – соs 38°; б) sin 5° + sin 55°.
Відповідь: а) sіn 8°; б) соs 25°.
3. Перетворіть в добуток:
а) соs 2α + соs 14α + соs 6α + соs 10α;
б) sin 4β + sin 10β + sin 22β + sin 16β .
Відповідь: а) 4соs 2α соs 4α соs 8α; б) 4 соs 3β соs 6β sіn 13β.
4. Доведіть тотожність:
а) ![]() ; б)
; б) ![]() .
.
VI. Домашнє завдання.
Розділ І § 10 (1; 3; 4). Запитання і завдання для повторення до розділу І № 63—65, 67, 68. Вправа: № 51 (1, 2, 3, 6, 7).
ТЕМА УРОКУ
Формули зведення
МЕТА УРОКУ
Дидактична:
- Вивчення формул зведення, формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
1. Відповіді на питання учнів, що виникли в процесі виконання домашнього завдання.
2. Самостійна робота.
Варіант 1
1. Спростіть  . (3 бали)
. (3 бали)
2. Знайдіть tg 2α, якщо tg α = - 0,4. (3 бали)
3. Спростіть  . (3 бали)
. (3 бали)
4. Обчисліть ![]() . (З бали)
. (З бали)
Варіант 2
1. Спростіть 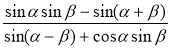 . (З бали)
. (З бали)
2. Знайдіть tg 2β, якщо tg β = 6. (З бали)
3. Спростіть 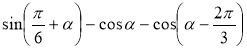 . (З бали)
. (З бали)
4. Обчисліть ![]() . (З бали)
. (З бали)
Відповідь: В-1. 1. –tgα tgβ . 2.![]() . 3. 0. 4.
. 3. 0. 4. ![]() .
.
В-2. 1. –сtgα tgβ. 2. ![]() . 3. 0. 4.
. 3. 0. 4. ![]() .
.
IІI. Сприймання і усвідомлення формул зведення.
Тригонометричні функції чисел виду ![]() ± α, π ± α;
± α, π ± α; ![]() ± α, 2π ± α можуть бути виражені через функції кута α за допомогою формул, які називаються формулами зведення.
± α, 2π ± α можуть бути виражені через функції кута α за допомогою формул, які називаються формулами зведення.
Користуючись формулами тригонометричних функцій суми (різниці) двох чисел, можна довести формули зведення:
|
для синуса
|
для косинуса
|
|
для тангенса і котангенса
|
|
Формули зведення запам'ятовувати необов'язково. Для того щоб записати будь-яку з них, можна користуватися таким правилом:
1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < α < ![]() .
.
2) Якщо в лівій частині формули кут дорівнює ![]() ± α,
± α, ![]() ± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується.
± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується.
Розглянемо приклади.
Приклад 1. Виразимо tg(π – α) через тригонометричну функцію кута α. Якщо вважати, що α — кут І чверті, то π – α буде кутом II чверті. У II чверті тангенс від'ємний, отже, у правій частині рівності слід поставити знак «мінус». Для кута π – α назва функції «тангенс» зберігається. Тому.
tg (π – α) = - tg α.
За допомогою формул зведення знаходження значень тригонометричних функцій будь-якого числа можна звести до знаходження значень тригонометричних функцій чисел від 0 до ![]() .
.
Приклад 2. Знайдемо значення sіn ![]() .
.
Маємо: 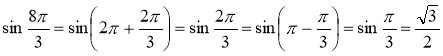 .
.
Виконання вправ______________________________
1. Приведіть до тригонометричних функцій числа а:
а)![]() ; б)
; б)![]() ; в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є)
; в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є)![]() .
.
Відповідь: а) соs α; б) - sіn α; в) - ctgα; г) tg α; д) - sіn α; є) сtg α.
2. Знайдіть:
а) sіn ![]() ; б) соs
; б) соs ![]() ; в) tg
; в) tg ![]() ; г) sіn
; г) sіn ![]() .
.
Відповідь: а) ![]() ; б) -
; б) - ![]() ; в) -
; в) - ![]() ; г)
; г) ![]() .
.
3. Спростіть:
а)  ; б)
; б)  .
.
Відповідь: а) 1. б) –1.
4. Доведіть, що
а)  , б)
, б) 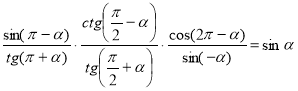 .
.
IV. Домашнє завдання.
Розділ І § 10 (2). Запитання і завдання для повторення до розділу І № 66. Вправи № 52 (12), № 26.
ТЕМА УРОКУ
Побудова графіків тригонометричних функцій
МЕТА УРОКУ
Дидактична:
- Побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Вивчення їх властивостей.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевірка домашнього завдання.
1. Один учень відтворює розв'язування вправи № 24 (1—3).
2. Фронтальна бесіда:
1) Назвіть явища в природі, які періодично повторюються.
2) Дайте означення періодичної функції.
3) Якщо функція у = f(x) має періодом число Т, то чи буде періодом цієї функції число 2Т, 3T...? Відповідь обґрунтуйте.
4) Знайдіть найменший додатний період функцій:
a) y = cos![]() ; б) y = sin
; б) y = sin ![]() ; в) у = tg
; в) у = tg ![]() ; г) у =
; г) у = ![]() .
.
5) Чи періодична функція у = З? Якщо так, то вкажіть період цієї функції.
ІII. Побудова графіка функції у = sin х.
Для побудови графіка функції у = sin x скористаємось одиничним колом. Побудуємо одиничне коло радіусом 1 см (2 клітинки). Праворуч побудуємо систему координат, як на рис. 57.
На вісь ОХ нанесемо точки ![]() ; π;
; π; ![]() ; 2π (відповідно 3 клітинки, 6 клітинок, 9 клітинок, 12 клітинок). Розділимо першу чверть одиничного кола на три рівні частини і на стільки ж частин відрізок
; 2π (відповідно 3 клітинки, 6 клітинок, 9 клітинок, 12 клітинок). Розділимо першу чверть одиничного кола на три рівні частини і на стільки ж частин відрізок ![]() осі абсцис. Перенесемо значення синуса до відповідних точок осі ОХ. Одержимо точки, які треба з'єднати плавною лінією. Потім розділимо другу, третю і четверту чверть одиничного кола також на три рівні частини і перенесемо значення синуса до відповідної точки осі ОХ. Послідовно з'єднавши всі отримані точки, одержимо графік функції у = sin х на проміжку [0;π].
осі абсцис. Перенесемо значення синуса до відповідних точок осі ОХ. Одержимо точки, які треба з'єднати плавною лінією. Потім розділимо другу, третю і четверту чверть одиничного кола також на три рівні частини і перенесемо значення синуса до відповідної точки осі ОХ. Послідовно з'єднавши всі отримані точки, одержимо графік функції у = sin х на проміжку [0;π].

Через те що функція у = sin x періодична з періодом 2π, то для побудови графіка функції у = sin x на всій прямій ОХ досить паралельно перенести побудований графік вздовж осі ОХ на 2π, 4π, 6π... одиниць вліво і вправо (рис. 58).

Крива, яка є графіком функції у = sin x, називається синусоїдою.
Побудова графіка функції у = cos x.
Як відомо, cos х = sin ![]() , тому у = cos x і у = sin
, тому у = cos x і у = sin ![]() — однакові функції. Для побудови графіка функції у = sin
— однакові функції. Для побудови графіка функції у = sin ![]() скористаємося геометрич-ними перетвореннями графіків: спочатку побудуємо (рис. 63) графік функції у = sin х, потім у = sin (-х) і наприкінці у = sin
скористаємося геометрич-ними перетвореннями графіків: спочатку побудуємо (рис. 63) графік функції у = sin х, потім у = sin (-х) і наприкінці у = sin ![]() .
.

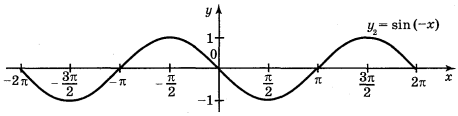

IV. Побудова графіка функції у = tg x.
Графік функції у = tg x побудуємо за допомогою лінії тангенсів на проміжку ![]() , довжина якого дорівнює періоду π цієї функції. Побудуємо одиничне коло радіусом 2 см (4 клітинки) і проведемо лінію тангенсів. Праворуч побудуємо систему координат, як на рис. 68.
, довжина якого дорівнює періоду π цієї функції. Побудуємо одиничне коло радіусом 2 см (4 клітинки) і проведемо лінію тангенсів. Праворуч побудуємо систему координат, як на рис. 68.
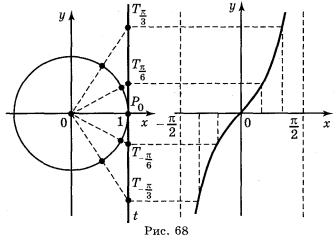
На вісь ОХ нанесемо точки ![]() ;
; ![]() (6 клітинок). Розділимо першу і четверту чверть кола на 3 рівні частини і на стільки ж частин кожний із відрізків
(6 клітинок). Розділимо першу і четверту чверть кола на 3 рівні частини і на стільки ж частин кожний із відрізків ![]() і
і ![]() . Знайдемо значення тангенсів чисел
. Знайдемо значення тангенсів чисел ![]() ;
; ![]() ; 0;
; 0; ![]() ;
; ![]() за допомогою лінії тангенсів (ординати точок
за допомогою лінії тангенсів (ординати точок ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() лінії тангенсів). Перенесемо значення тангенсів до відповідних точок осі ОХ. Послідовно з'єднавши всі отримані точки, одержимо графік функції у = tg x на проміжку
лінії тангенсів). Перенесемо значення тангенсів до відповідних точок осі ОХ. Послідовно з'єднавши всі отримані точки, одержимо графік функції у = tg x на проміжку ![]() .
.
Через те що функція у = tg x періодична з періодом π, для побудови графіка функції у = tg x на всій прямій ОХ досить паралельно перенести побудований графік вздовж осі ОХ на π, 2π, 3π, 4π... одиниць вліво і вправо (рис. 69).
Графік функції у = tg x називається тангенсоїдою.

V. Побудова графіка функції у = ctg x.
Графік функції у = ctg x легко одержати, скориставшись формулою ctg x = tg ![]() і двома геометричними перетвореннями (рис. 74): симетрія відносно осі ΟΥ паралельне перенесення вздовж осі ОХ на
і двома геометричними перетвореннями (рис. 74): симетрія відносно осі ΟΥ паралельне перенесення вздовж осі ОХ на ![]() .
.

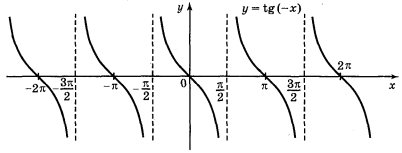

Властивості вивчених тригонометричних функцій зручно записати в таблицю 5.
Таблиця 5

IV. Домашнє завдання.
Розділ І § 6. Запитання і завдання для повторення до розділу І № 50-51. Вправи № 28 (а-г).
ТЕМА УРОКУ
Геометричні перетворення графіків тригонометричних функцій
МЕТА УРОКУ
Дидактична:
- Удосконалювати вміння та навички побудови графіків функцій, за допомогою геометричних перетворень;
- Ознайомити студентів з можливостями використання прикладного програмного забезпечення для побудови графіків функцій.
Розвиваюча:
- розвивати творчі здібності студентів;
- розвивати просторову уяву.
Виховна:
- виховувати інтерес до математики як науки;
- виховувати графічну культуру, культуру математичної мови та письма.
ТИП УРОКУ
Бінарний урок узагальнення та систематизації знань (математика + інформатика).
ОБЛАДНАННЯ
- Матеріал з даної теми.
- Комп’ютери, діапроектор, екран.
- Програмне забезпечення (MS Power Point, Advanced Grapher 2.2).
- Дошка, маркери, лінійка, функціональні лінійки (15 шт), індивідуальні картки.
ПЛАН УРОКУ
- Організаційна частина.
- Актуалізація опорних знань.
- Узагальнення знань студентів з даної теми.
- Розв’язування прикладів.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
(Представлення викладачів).
ІІ. Фронтальне опитування:
На попередніх уроках ми з’ясували, який вигляд мають графіки тригонометричних функцій.
Отже,
- Що є графіком функції y=sin x ?
(Слайд № 2)
Синусоїда.
- Як з графіка функції y=sin x отримати графік y=cos x?
(Слайд № 3)
Треба виконати паралельне перенесення графіка y=sin x вліво на ![]() одиниць, виходячи з рівняння
одиниць, виходячи з рівняння ![]() .
.
- Який період мають графіки y=sin x, y=cos x?
![]() .
.
- Що є графіком функції y=tg x ?
(Слайд № 4)
Тангенсоїда.
- Через які значення проходять асимптоти графіка y=tg x?
Через точки виду ![]() .
.
- Які перетворення графіків функцій ви знаєте?
Симетрія, паралельне перенесення, деформація(стиск, розтяг).
Таким чином, ми з’ясували вигляд графіків основних тригонометричних функцій, але на практиці, наприклад, в фізиці при вивченні гармонійних коливань, графіка напруги необхідно вміти будувати графіки більш складних функцій.
(Слайд № 5, 6)
Наприклад, Що спільного між: гойдалками, музикою та світлом? Це коливальні процеси, які описуються рівнянням
![]() .
.
Побудувати графік даного типу можна, виконавши геометричні перетворення над графіком y=sin x.
ІІІ. Отже, тема уроку: Геометричні перетворення графіків тригонометричних функцій.
(На екрані з’являється тема заняття . Слайд № 7).
Завдання № 1 (УСНО)
(Слайд № 8)
Проаналізуйте малюнок і назвіть геометричні перетворення, які виконуються для побудови графіків.
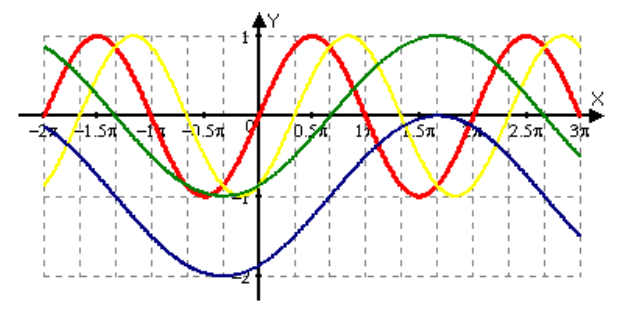
![]() 1)
1) ![]()
![]() 2)
2) ![]() - паралельне перенесення графіка вправо на
- паралельне перенесення графіка вправо на ![]() одиниць.
одиниць.
![]() 3)
3) ![]() розтяг попереднього графіка вздовж осі ОХ в 2 рази
розтяг попереднього графіка вздовж осі ОХ в 2 рази
4) ![]() паралельне перенесення останнього графіка
паралельне перенесення останнього графіка
![]() вниз на одиницю.
вниз на одиницю.
IV.
(Слайд № 9-13)
Завдання № 2
Побудувати графіки:
![]()
Розв’язання
![]() 1)
1) ![]()
![]() 2)
2) ![]() - стиск попереднього графіка вздовж осі ОY в 2 рази
- стиск попереднього графіка вздовж осі ОY в 2 рази
3) ![]() паралельне перенесення другого графіка
паралельне перенесення другого графіка
![]() вліво на
вліво на ![]() одиниць (4 клітинки)
одиниць (4 клітинки)
![]() 4)
4) ![]() паралельне перенесення останнього графіка вгору на одиницю.
паралельне перенесення останнього графіка вгору на одиницю.

![]()
![]() 1)
1) ![]()
![]() 2)
2) ![]() - стиск попереднього графіка вздовж осі ОY в 3 рази
- стиск попереднього графіка вздовж осі ОY в 3 рази
3) ![]() паралельне перенесення другого графіка
паралельне перенесення другого графіка
![]() вправо на
вправо на ![]() одиниць.
одиниць.
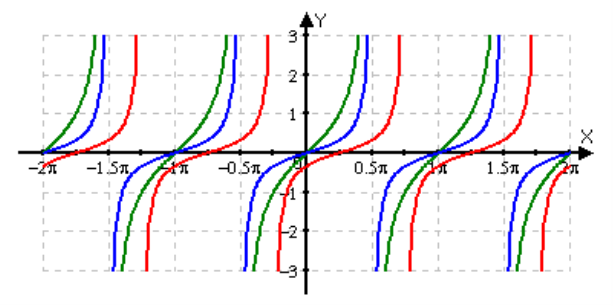
Завдання № 3
(Слайд №14)
Серед графіків, які зображено на малюнках 1- 4 назвіть графік функції:
а) y=2sin x+2
б) y=2cos 2x
в) ![]()
г) ![]()
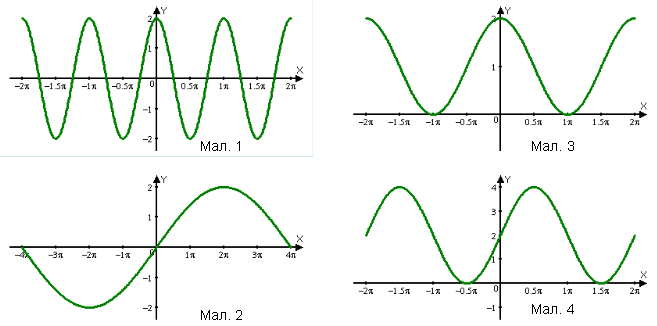
Відповідь: а) мал.. 4; б) мал.. 1; в) мал.. 2; г) мал.. 3.
Завдання № 4 (Слайд № 15)
Виконати в зошиті індивідуальне завдання з картки та перевірити правильність побудови за допомогою комп’ютера (програма Advanced Grapher 2.2).
(Роздаються картки по одній на 2 студентів. Вони виконують побудову в зошиті. Пересідають за комп’ютери та будують ту саму функцію за допомогою запропонованої програми. Порівнюють результати).
V. Підсумки. (Оголошення оцінок). Д/з.:
(Слайд № 16)
- 1. Побудувати графіки функцій:
![]() ;
; ![]()
- 2. Повторити значення синусів, косинусів, тангенсів від 0 до 1800.
ТЕМА УРОКУ
Поняття про обернену функцію. Обернені тригонометричні функції, їх властивості та побудова
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «обернена функція», розглянути вигляд та розкрити властивості обернених тригонометричних функцій.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
Тригонометричні функції та їх властивості.
ІІІ. 1. Поняття оберненої функції
Функція f, яка має обернену, називається оборотною.
Оберненою до даної оборотної функції ![]() називається така функція
називається така функція ![]() , яка кожному
, яка кожному ![]() із множини значень функції
із множини значень функції ![]() ставить у відповідність єдине число х із її області визначення.
ставить у відповідність єдине число х із її області визначення.
Графік функції ![]() , оберненої до функції
, оберненої до функції ![]() , симетричний графіку
, симетричний графіку ![]() відносно прямої
відносно прямої ![]() .
.
Алгоритм знаходження оберненої функції:
-
З’ясовуємо, чи є функція
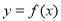 оборотною на всій області визначення. Якщо ні, то виділяємо підмножину області визначення, де існує функція обернена до
оборотною на всій області визначення. Якщо ні, то виділяємо підмножину області визначення, де існує функція обернена до 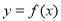 .
.
-
Розв’язуємо рівняння
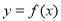 відносно змінної х, тобто знаходимо функцію
відносно змінної х, тобто знаходимо функцію 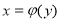 , яка є оберненою до
, яка є оберненою до 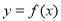 .
.
-
Міняємо позначення змінних
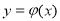 .
.
2.Функція обернена до ![]() .
.
Розглянемо ![]() на проміжку
на проміжку ![]() функція монотонна.
функція монотонна.
Відобразимо отриманий графік відносно ![]() .
.
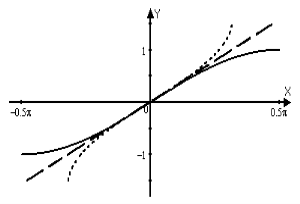
Властивості:
1. ![]()
2. ![]()
3. непарна, ![]()
4. неперіодична
5. зростаюча
6. ![]()
Арксинусом числа а називається такий кут х, синус якого дорівнює а.
![]()
3. Функція обернена до ![]() .
.
Розглянемо ![]() на проміжку
на проміжку ![]() функція монотонна.
функція монотонна.
Відобразимо отриманий графік відносно ![]() .
.

Властивості:
1. ![]()
2. ![]()
3. не є парна, не є непарна ![]()
4. неперіодична
5. спадаюча
6. ![]()
4. Функція обернена до ![]() .
.

Властивості:
1. ![]()
2. ![]()
3. непарна, ![]()
4. неперіодична
5. зростаюча
6. ![]()
5. Функція обернена до ![]() .
.
Властивості:
1. ![]()
2. ![]()
 3. не є парна, не є непарна
3. не є парна, не є непарна ![]()
4. неперіодична
5. спадаюча
6. ![]()
ІV. Обчислити:
1) ![]() так як
так як ![]() .
.
2) 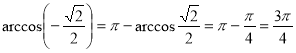
3) ![]()
4) ![]()
5) ![]()
6) 
7) ![]()
8) ![]()
9) ![]()
V. Д/з Шкіль ст.. 125 № 12(1-10).
ТЕМА УРОКУ
Розв’язування найпростіших тригонометричних рівнянь
МЕТА УРОКУ
Дидактична:
- Ознайомити учнів з поняттям «тригонометричні рівняння » та розкрити методи їх розв’язання.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Перевіряю Д/з. Запитую означення обернених тригонометричних функцій.
ІІІ. 1. Тригонометричними називаються рівняння, у яких невідома (змінна) входить лише під знак тригонометричних функцій.
|
Приклади |
Контрприклади |
|
|
|
|
|
|
|
|
|
Тригонометричні рівняння або зовсім не мають розв’язків, або мають безліч розв’язків (так як функція періодична).
2. ![]()
Будуємо в одній системі координат графіки ![]() ,
, ![]() .
.
Якщо ![]() , тобто
, тобто ![]() і
і ![]() пряма і синусоїда не перетинаються. Тому рівняння
пряма і синусоїда не перетинаються. Тому рівняння ![]() не має розв’язків.
не має розв’язків.
Якщо ![]() , тобто
, тобто ![]() , рівняння має безліч коренів. Знайдемо корені рівняння на
, рівняння має безліч коренів. Знайдемо корені рівняння на ![]() , а потім скористаємося періодичністю.
, а потім скористаємося періодичністю.
![]() перетинає синусоїду в точках Р1 та Р2. Оскільки розв’язання рівняння зводиться до знаходження числа , синус якого дорівнює а, то цим числом є
перетинає синусоїду в точках Р1 та Р2. Оскільки розв’язання рівняння зводиться до знаходження числа , синус якого дорівнює а, то цим числом є ![]() , якщо воно міститься на відрізку
, якщо воно міститься на відрізку![]() .
.

Абсциса точки Р2 - ![]() .
.
Якщо врахувати періодичність, то
![]()
![]()
Ці множини можна об’єднати в одну
![]()
Часткові випадки:
![]()
![]()
![]()
 3.
3. ![]()
Якщо ![]() , то рівняння не має розв’язків.
, то рівняння не має розв’язків.
Якщо ![]() , тобто
, тобто ![]() , рівняння має безліч коренів.
, рівняння має безліч коренів.
![]()
![]()
Ці множини можна об’єднати в одну
![]()
Часткові випадки:
![]()
![]()
![]()
4. ![]()

Знайдемо корені рівняння на ![]() , а потім скористаємося періодичністю.
, а потім скористаємося періодичністю.
![]()
Часткові випадки:
![]()
![]()
![]()
5. ![]()
Для розв’язання даного рівняння треба розв’язати рівняння ![]() .
.
IV. Розв’язати рівняння:
1. ![]()
![]()
![]()
2. ![]()
![]()
![]()
3. ![]()

![]()
![]()
4. ![]()
![]()
![]()
5. ![]()
![]()
![]()
V. Д/з. Шкіль стр. 126 № 1(4,6,8,10,12,14,18)
ТЕМА УРОКУ
Деякі способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших
МЕТА УРОКУ
Дидактична:
- Ознайомити студентів з методами розв’язання рівнянь, що відрізняються від найпростіших; розглянути нові види рівнянь (лінійні, однорідні).
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. 4 студенти біля дошки показують розв’язання домашніх прикладів.
Математичний диктант.
|
І варіант |
ІІ варіант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ІІІ. 1. Алгебраїчний метод (зведення до однієї тригонометричної функції).
Наприклад, ![]()
З основної тригонометричної тотожності ![]() .
.
Тоді ![]()
![]()
![]()
![]()
Маємо 2 рівняння ![]()
![]()
2.Спосіб розкладання на множники:
- Перенести усі члени рівняння у ліву частину;
- Представити отриманий вираз у вигляді добутку;
- Використати достатню та необхідну умову рівності дробу нулю.
![]()
За формулами зведення ![]()
![]() За формулою
За формулою ![]() .
.
Отримаємо ![]()
![]()
![]()
![]()
![]()
![]()
- Спосіб розв’язування однорідних рівнянь.
Рівняння є однорідним, якщо його ліва частина є многочлен, у кожному члені якого сума показників степенів синуса і косинуса одного й того самого аргументу однакова, а права – нуль.
Алгоритм розв’язання:
-
Ділять обидві частини на
 ;
;
-
Переконуються, що
 .
.
![]()
![]() .
.
![]()
![]()
- Спосіб введення допоміжного аргументу.
Даним способом користуються при розв’язувані лінійних рівнянь, якими називаються рівняння виду ![]() .
.
![]()
![]() Представимо
Представимо ![]() ,
, ![]()
 Помножимо на
Помножимо на ![]() .
.
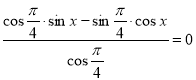
![]()
![]()
![]()
Частіше використовують заміну  ;
;  .
.
- Спосіб піднесення до квадрата.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Графічний спосіб.
![]() або
або ![]()
Точки перетину даних графіків є корені даного рівняння.

ІV. Розв’язати рівняння:
1) ![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]() або
або ![]()
![]()
![]()
3) ![]()
Замінимо тангенсом половинного аргументу.
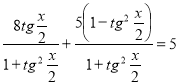
![]()
![]()
![]()
![]() або
або ![]()
![]()
![]()
4) ![]()
![]()
![]()
![]() або
або ![]()
![]()
![]()
![]()
![]()
ІV. Д/з Шкіль стр. 127 № 2(1,6,10,22).
ТЕМА УРОКУ
Практична робота
МЕТА УРОКУ
Дидактична:
- Навчити застосовувати розглянуті методи розв’язування тригонометричних рівнянь, навчити розрізняти рівняння за їх видами.
Розвиваюча:
- розвивати аналітичне мислення.
ТИП УРОКУ
Засвоєння знань, умінь та навичок.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Застосування матеріалу в стандартних умовах.
- Застосування матеріалу в нестандартних умовах.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
І. Вітаюся. Відмічаю відсутніх.
ІІ. Фронтальне опитування:
- Які рівняння називаються однорідними?
Рівняння є однорідним, якщо його ліва частина є многочлен, у кожному члені якого сума показників степенів синуса і косинуса одного й того самого аргументу однакова, а права – нуль.
- Які рівняння називаються лінійними?
Рівняння виду ![]() називаються лінійними рівняннями.
називаються лінійними рівняннями.
- Перерахуйте способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших.
- Алгебраїчний метод (зведення до однієї тригонометричної функції), спосіб розкладання на множники, спосіб розв’язування однорідних рівнянь, спосіб введення допоміжного аргументу, спосіб піднесення до квадрата, графічний спосіб.
- Які недоліки алгебраїчного способу?
Громіздкий.
- Які недоліки графічного способу?
Неточний.
ІІІ. Розв’язати рівняння:
1. ![]()
![]()
![]()
![]()
![]()
Введемо позначення ![]() , тоді
, тоді
![]()
![]()
![]()
![]()
![]()
![]()
2. ![]()
Замінимо синус та косинус тангенсом половинного аргументу

![]()
![]()
Позначимо ![]() , тоді
, тоді
![]()
![]()
Відповідь: розв’язків не має.
3. ![]()
![]()
![]()
![]()
Погрупуємо та винесемо спільний множник за дужки
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ІV. Розв’язати рівняння:
4.
![]()
![]() Поділимо на
Поділимо на ![]()
![]()
![]()
![]()
![]()
![]()
![]()
5. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Самостійно розв’язати рівняння:
1) ![]()
2) ![]()
3) ![]()
V. Д/з. Шкіль стр. 127 № 2(41, 17)
41) 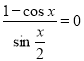 17)
17) ![]()
ТЕМА УРОКУ
Розв'язування тригонометричних нерівностей
МЕТА УРОКУ
Дидактична:
- Формування умінь учнів розв'язувати тригонометричні нерівності.
ТИП УРОКУ
Засвоєння нових знань.
ПЛАН УРОКУ
- Організаційна частина.
- Перевірка Д/з. Актуалізація опорних знань.
- Повідомлення нового матеріалу.
- Засвоєння нового матеріалу.
- Підсумки. Домашнє завдання.
ХІД УРОКУ
 І. Перевірка домашнього завдання.
І. Перевірка домашнього завдання.
1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання.
2. Фронтальна бесіда з учнями з використанням рис. 135.
1) Які дуги відповідають нерівностям:
tg t > a, tg t < a, tg t > - a, tg t < - a?
2) Нехай <AOB = ![]() . Запишіть у вигляді нерівності дугу, яка відповідає нерівності:
. Запишіть у вигляді нерівності дугу, яка відповідає нерівності:
tg x ![]() a, tg x
a, tg x ![]() a, tg x
a, tg x ![]() - a, tg x
- a, tg x ![]() -a.
-a.
3) Розв'яжіть нерівності:
tg x ![]() 0; tg x
0; tg x ![]() 0; ctg x
0; ctg x ![]() 0; ctg x
0; ctg x ![]() 0.
0.
II. Формування умінь розв'язувати тригонометричні нерівності.
1. Розв'яжіть нерівності:
а) 2sin ![]()
![]() –
– ![]() ; б) 2sin
; б) 2sin ![]()
![]() l; в) 3ctg
l; в) 3ctg ![]() > –
> – ![]() ; г)
; г) ![]() sin
sin ![]()
![]() 1.
1.
Відповідь: а) ![]() , п
, п ![]() Z; б)
Z; б) ![]() , п
, п ![]() Z;
Z;
в) ![]() , п
, п ![]() Z; г) [4πп; π + 4πп], п
Z; г) [4πп; π + 4πп], п ![]() Z.
Z.
2. Розв'яжіть нерівності:
a) sin![]() cos
cos![]()
![]() -
-![]() ; б) 2sin2
; б) 2sin2![]() <
<![]() ;
;
в) sin 2х + ![]() cos 2х < 0; г) sin2 x + 2sin x < 0.
cos 2х < 0; г) sin2 x + 2sin x < 0.
Відповідь: а) ![]() , п
, п ![]() Z; б)
Z; б) ![]() , п
, п ![]() Z;
Z;
в) ![]() , п
, п ![]() Z; г) (-π + 2πn; 2πn), п
Z; г) (-π + 2πn; 2πn), п ![]() Z.
Z.
II. Самостійна робота.
Варіант 1
Розв'яжіть нерівності:
а) 2sin х < – 1. (4 бали) б) – 3tgx ![]()
![]() . (4 бали) в) 2 cos
. (4 бали) в) 2 cos ![]() <
< ![]() . (4 бали)
. (4 бали)
Варіант 2
Розв'яжіть нерівності:
a) 2cosx ![]()
![]() . (4 бали) б) -
. (4 бали) б) - ![]() tgx
tgx ![]() 3. (4 бали) в) 2 sin
3. (4 бали) в) 2 sin ![]()
![]() -1 . (4 бали)
-1 . (4 бали)
Відповідь: B-l: a) ![]() , п
, п ![]() Z; б)
Z; б) ![]() , п
, п ![]() Z;
Z;
в) ![]() , п
, п ![]() Z
Z
B-2: a) ![]() , п
, п ![]() Z; б)
Z; б) ![]() , п
, п ![]() Z;
Z;
в) ![]() , п
, п ![]() Z.
Z.
IV. Узагальнення відомостей про розв'язання тригонометричних нерівностей.
Питання
1. При яких значеннях а має розв'язки нерівність a) sin t > а; б) sin t < a?
2. При яких значеннях b має розв'язки нерівність a) cos t > b; б) sin t < b?
3. Як знайти розв'язки нерівностей
a) sin t > а; б) sin t < а; в) cos t > b; г) cos t < b?
4. Як знайти розв'язки нерівностей
a) tg t > а; б) tg t < а; в) ctg t > b; г) ctg t < b?
У ході обговорення питань заповнюється таблиця 12 на дошці і в зошитах учнів.
V. Підведення підсумків уроку.
VI. Домашнє завдання.
Розв'яжіть нерівності:
a) sin ![]() <
< ![]() ; б) cos2
; б) cos2 ![]() - sin2
- sin2 ![]()
![]() - 0,5; в) sin х +
- 0,5; в) sin х + ![]() cos х > 0 .
cos х > 0 .
Таблиця 12


1
-
Дякую


про публікацію авторської розробки
Додати розробку







 ;
; 
 .
.







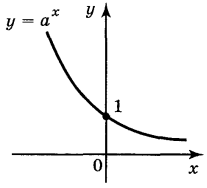

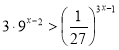
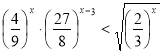


 , тоді
, тоді