Урок "Застосування похідної до дослідження функції"

          Тема уроку: Застосування  похідної до дослідження функцій.

Мета уроку:

Навчальна: повторити, систематизувати й узагальнити знання учнів про похідну функції; закріпити навички застосування похідної до дослідження функцій; продовжити роботу з формування вмінь виконувати дії відповідно до складеної схеми та зображувати ескізи графіків функцій за здобутими результатами дослідження її властивостей;

Розвивальна: розвивати логічне мислення, навички практичного використання набутих теоретичних знань, вміння орієнтуватись у нестандартних ситуаціях;

Виховна: виховувати інтерес до математики, точність та послідовність при виконанні вправ, прагнення до поглиблення та удосконалення знань з математики.

Тип уроку: урок узагальнення та систематизація знань.

Метод проведення: бесіда, демонстраційний, проблемно – пошуковий, груповий.     

Міжпредметні зв'язки: Інформатика "Інформаційні технології у навчанні"; Всесвітня історія "Культура XVII–XIIXст."

Обладнання: мультимедійні засоби навчання, тематична презентація в MSPowerPoint, інтерактивні навчальні модулі в LearningApps.org, картки самооцінювання.

Література:

1. Г.П. Бевз. В.Г. Бевз. Математика. 11 клас. Рівень стандарту. – Київ: "Генеза", 2013.

2. Збірник завдань для державної підсумкової атестації з математики: 11 – й кл. /О.І. Глобін та ін. – К. : Центр навч. – метод. л – ри, 2013.

3. О.О. Старова. Алгебра та початки аналізу. 11 клас. Рівень стандарту. – Харків: "Основа", 2011.

 

Хід уроку

І. Організаційний етап

Організація уваги учнів. Перевірка готовності групи до заняття.

Учням роздано аркуші оцінювання з переліком завдань та кількістю балів, які можна набрати за їх виконання. Кожен учень вписує у аркуш оцінювання своє прізвище та ім’я. Упродовж уроку учні самостійно занотовують кількість набраних балів за кожен вид роботи.

 

ІІ. Перевірка домашнього завдання

Творче домашнє завдання. Презентація історичного дослідження на тему "Вклад вчених у розвиток диференціального числення".

 

ІІІ. Повідомлення теми, мети і завдань уроку

Фундаментом математики служить математичний аналіз. Основою математичного аналізу є взаємопов’язані за змістом розділи – диференціальне та інтегральне числення.

Одним з важливих понять математичного аналізу є похідна. І сьогодні, у центрі уваги – дослідження функції за допомогою похідної.

 

ІV. Мотивація навчальної діяльності

Сучасні фахівці повинні добре володіти математичним апаратом, який має надзвичайне значення для багатьох професій. Використання теорії диференціального числення є важливим для розвитку сучасної економіки, бізнесу, фінансової справи. 

Тому девізом нашого уроку будуть слова Ісаака Ньютона "Досвід – це не те, що трапляється з вами, а те, що ви робите з тим, що трапляється з вами"

 

V. Актуалізація знань, умінь та навичок

-  Інтерактивна гра "Відгадай мене скоріше???" (з використанням он-лайн сервісу LearningApps.org).

Необхідно пригадати основні поняття з теми: "Похідна та її застосування", які ми вивчали на попередніх уроках, та вписати пропущені слова у математичний кросворд.

 

 

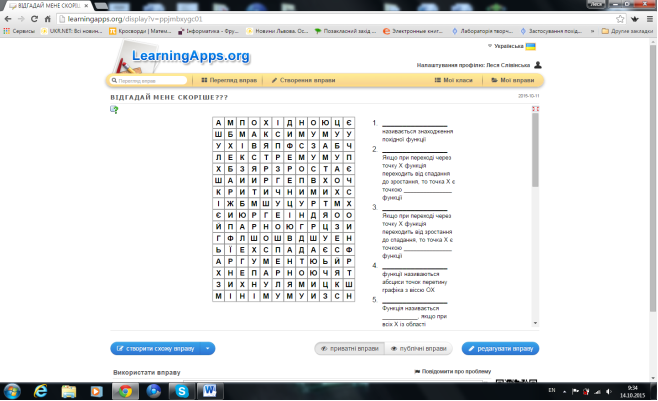
Перелік запитань:

1. Диференціюванням називається знаходження похідної функції.
2. Якщо при переході через точку х функція переходить від спадання до зростання, то точка х є точкою мінімуму функції.
3. Якщо при переході через точку х функція переходить від зростання до спадання, то точка х є точкою максимуму функції.
4. Нулями функції називаються абсциси точок перетину графіка з віссю О_х.
5. Функція називається парною, якщо при всіх х із області визначення функції виконується рівність:  f(-х)=f(х).
6. Якщо для всіх х з даного проміжку виконується рівність f '(х), то функція f спадає на даному проміжку.
7. Критичними точками функції називаються точки, в яких похідна функції дорівнює нулю, або не існує.
8. Область визначення функції – це множина значень, яких набуває аргумент.
9. Функція називається непарною, якщо при всіх х із області визначення функції виконується рівність: f (-х)=-f(х).
10.  Похідною функції f у точці х₀  називається число, яке дорівнює границі відношення приросту функції до приросту аргументу, при умові, що приріст аргументу прямує до нуля.
11.  Якщо для всіх х з даного проміжку виконується рівність f '(х)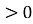, то функція f зростає на даному проміжку.
12.  Точками екстремуму називаються точки максимуму і точки мінімуму функції.

 

V. Повторення та аналіз основних знань

1. Розв'язування вправ. Математична естафета.

Знаходження похідних елементарних функцій

 

3х2 + 5	2х2 + 10х	2х7 - 8х2 + 12
х 6	х10	3х3
2х3 – 4х	6х11	10х9 +9
4х4	4х5- 99	4х2 + 4х - 2
5х6 -3х2+7	7х2 -2х7+14	20х+20
х 100	5х8 - 8х	5х10

 

2. Математичний пазл "Істинна чи хибність".

За даним графіком функцій визначити істинність твердження, відкриваючи пазли он-лайн сервісу LearningApps.org.

 

 

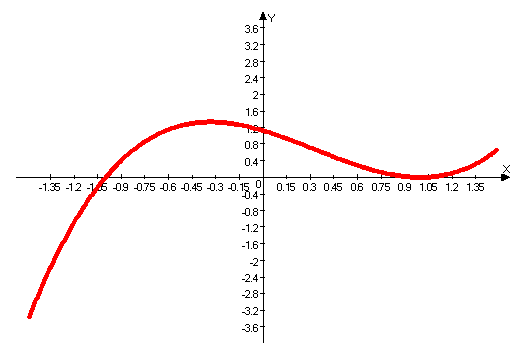
1) Функція визначена на всій числовій прямій. (Істина)

2) Функція не є ні парною, ні непарною. (Істина)

3) Функція періодична. (Хибність)

4) Нулями функції є точки х=1,5. (Хибність)

5) Дана функція має три критичні точки. (Хибність)

6) Функція зростає на проміжку [0.33; 1]. (Хибність)

7) Функція спадає на проміжку [ -0.33; 1]. (Істина)

8) Функція має мінімум в точці х=1. (Істина)

9) Функція має максимум в точці х=-0.33. (Істина)

10) Графік функції не перетинає вісь ординат. (Хибність)

 

 

При достовірному відкритті учнями математичного пазлу - з'явиться дане зображення у 3 – ох вимірному просторі.

 

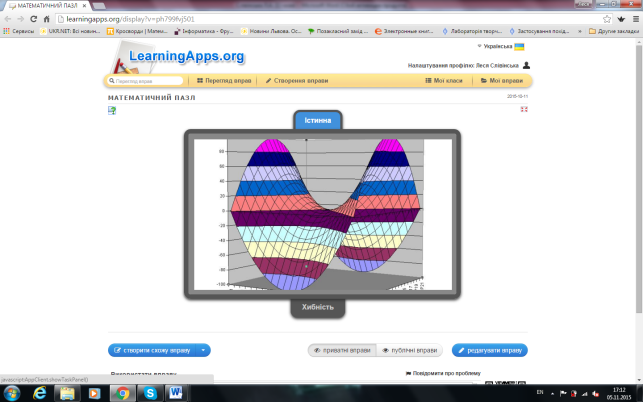
  VI. Узагальнення та систематизація знань

Робота в групах. Дидактична гра "Шифрувальники"

Учні об’єднуються в 2 групи, вибираючи колір групи (блакитний, жовтий). Кожна група отримує графік функції. Необхідно "зашифрувати"  його за допомогою описування властивостей даної функції, достатніх для побудови графіка функції:

1. Проміжки спадання;
2. Проміжки зростання;
3. Нулі функції;
4. Координати точок максимуму;
5. Координати точок мінімуму;
6. Координати точки перетину графіка з віссю ОУ.

Обидві групи обмінюються "шифровками" і кожна з груп за описаними властивостями функції будує її графік. Після цього побудований графік звіряється зі зразком.

За правильне "шифрування" члени груп отримують по 2 бали, за правильне "розшифрування" – по 3 бали.

 

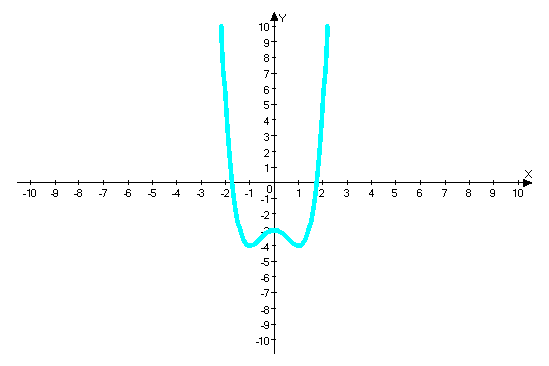
Графік функції для групи блакитного кольору: y=x⁴-2x²-3.

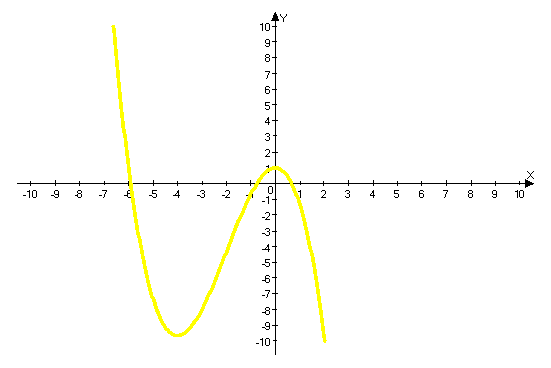
Графік функції для групи жовтого кольору: 

VIІ. Підсумки уроку

Учні рахують бали в аркуші оцінювання; згідно таблиці відповідності переводять їх у 12–бальну систему оцінювання і результати повідомляють викладачу. Учні самостійно аналізують свою роботу на уроці. Викладач виставляє і коментує оцінки.

 

VIІI. Домашнє завдання

Повторити §10 (ст. 78). Виконати вправи  № 364 (а – г), № 365 (а – г) (ст. 85).

 

  

Додаток

Аркуш оцінювання

 

Прізвище, ім'я учня
Номер завдання	Назва завдання	Кількість балів	Усього балів	Кількість набраних балів	Оцінка за 12-бальною шкалою
1	Творче домашнє завдання	3 бали	3
2	Вправа "Відгадай мене скоріше ???"	по 1 балу	12
3	Математична естафета	по 1 балу	18
4	Математичний пазл	по 1 балу	10
5	Самостійна робота: а) шифрування графіка; б) розшифрування графіка	2 бали 3 бали	5
Загальна кількість балів			48

 

 

Таблиця відповідності балів

Кількість набраних балів	Оцінка за 12 – бальною системою оцінювання навчальних досягнень учнів
0-3	1
4-6	2
7-9	3
10-12	4
13-15	5
16-18	6
19-23	7
24-28	8
29-33	9
34-38	10
39-43	11
44-48	12