Інтерактивний урок "Рівняння з модулями"

 

План уроку.

I Організаційний момент.

II Повідомлення теми та мети уроку.

III Мотивація навчальної діяльності.

IV Прес-конференція.

1. Рівняння з модулями:
   • Історична довідка
   • «поміркуй» (розгадування кросворду)
2. Модуль числа. Найпростіші рівняння з модулями:
   • Розв’язування рівнянь.
   • Презентація групи.
   • Виконання тесту за комп’ютером.
3. Способи розв’язування рівнянь:
   • Презентація груп.

- Розкриття модуля за означенням.

- Піднесення обох частин рівняння до квадрату.

- Метод інтервалів.

- Графічний метод.

• Самостійна робота.

4. Рівняння, що містять модулі і параметри:
   • Способи розв’язування рівнянь.
   • Розв’язування рівнянь.
   • Самостійна робота.

V Рефлексія.

VI Домашнє завдання.

VII Підсумки навчальної діяльності.

VIII Самооцінка учнів. Оцінювання.

Тема: Рівняння з модулями.

Інтерактивний урок із застосуванням комп’ютерних технологій з алгебри та початків аналізу в 10 класі.

Мета: Систематизувати та узагальнити знання про рівняння з модулями.

Завдання:

• Навчальні
  1. відтворити знання про модуль, рівняння з модулям, його види, способи розв’язування;
  2. систематизувати та узагальнити навчальні досягнення учнів щодо розв’язання рівнянь з модулями;
  3. виробити і засвоїти навички і вміння розв’язувати рівняння з параметрами;
  4. оволодіти значним арсеналом методів дослідження.
• Розвивальні
  1. розвивати увагу, мислення, пам'ять культуру математичного мовлення;
  2. вміння працювати самостійно, вміння спілкуватись, допомагати іншим, аналізувати ситуацію, оцінювати свої дії та дії інших учнів;
  3. вміння і навички щодо розв’язування рівнянь, оформлення завдань;
  4. набути комунікативної компетентності;
  5. оволодіти інформаційно-комунікаційними технологіями.
     •    Виховні

1. виховувати уважність, кмітливість, акуратність, самостійність, дисциплінованість, самокритичність.

Тип уроку: Узагальнення та систематизація знань, умінь і навичок.

Обладнання:   Комп’ютери, роздавальний матеріал, таблиці.

Хід уроку.

I Організаційний момент (1 хв.)

II Повідомлення теми та мети уроку.

III Мотивація навчальної діяльності.

 

Минуле і майбутнє… Таємниці історії великих відкриттів і сучасні досягнення науки. Різні галузі застосування знань… Життя – найчарівніший дар природи, але, щоб воно приносило радість, потрібно навчитись працювати захоплено, прагнути полегшити свою працю та вдосконалити її звичні форми.

 Математика – це мова плюс міркування, це наче мова й логіка разом. Математика – це знаряддя для міркування – зазначає Р.Фейнман.

Сьогодні на уроці ми перенесемось у зачарований науковий світ. Уявимо, що ми на прес-конференції, де обговорюється питання «Рівняння з модулями». Поняття модуля необхідне для розуміння багатьох питань сучасної математики. Враховуючи те, що в учнів виникають певні труднощі під час розв’язування рівнянь, які містять модулі, та рівнянь, які містять і модулі, і параметри, ми сьогодні проводимо прес-конференцію по питанню «Рівняння з модулями».

Прес-конференція

1. Рівняння з модулями

• Історична довідка.

Математичні знання необхідні кожній людині незалежно від того, чим вона займається в житті.

Початок лічби губиться у глибині віків і належить до того періоду історії людства, коли ще не було письменництва. Писати людина навчилася тоді, коли досить далеко просунулась в умінні рахувати. Математичні знання в далекому минулому застосовувались до розв’язання щоденних задач, і саме практика значною мірою керувала всім подальшим розвитком математики.

Але для того, щоб математика залишалась знаряддям дослідів нових глибоких явищ, її треба систематично розвивати, відточувати розроблені нею методи дослідження та створювати нові. Розв’язування багатьох практичних задач зводиться до рівнянь.

Лінійні рівняння з одним невідомим вміли розв’язувати ще в давньому Вавилоні та Єгипті більш ніж 4 тис. років тому. Єгипетські жриці шукане невідоме число називали «хау» ( у перекладі – «куча» ) і позначали спеціальним знаком.

На зламі III-ΙV ст.. припадає діяльність Діофанта із Олександрії, який яскраво виділяється на тлі наукового застою незвичним талантом. Учений в основному займався рівняннями більш високих степенів.

 Історія зберегла дуже мало відомостей про Діофанта, навіть точно не встановлені роки його життя. Дещо про його життя і про те, скільки років він прожив, можна дізнатися з напису на могильній плиті.

Епітафія Діофанта.

Прах Діофанта гробниця ховає:

Вдивися – і камінь мудрим мистецтвом розкриє покійного вік.

З волі богів шосту частину життя був він дитина,

А ще половину шостої- стрів із пушком на  щоках.

Тільки минула сьома, з коханою він одружився.

З нею п’ять років проживши, сина діждався мудрець,

Та пів життя свого тішився батько лиш сином:

Рано могила дитину у батька забрала.

Років двічі по два батько оплакував сина.

А по роках цих і сам встрів він кінець свій печальний
Знак модуля числа  IXI ввів у 1841 році німецький математик
К. Вейєрштрасс (1815-1897 р.). Термін «модуль( від латинського modulus- міра) ввів значно раніше англійський математик Р.Котес (1682-1716 р.)

• «Поміркуй» (розгадування кросворду)

2. Модуль числа. Найпростіші рівняння з модулями.

• Презентація групи.
• Розв’язування рівнянь

Найпростіші рівняння розв’язуємо застосовуючи алгебраїчний та геометричний зміст модуля.

ПРИКЛАД 1 Розв’язати рівняння

Розв’язання

Міркуючи як і в попередньому прикладі, маємо:

Очевидно, що . Тому маємо
х+5=3, х=-2;   -(х+5)=3, х= -8.

ПРИКЛАД 2 Розглянемо рівняння .

Розв’язати його – означає знайти всі точки координатної прямої, що лежить на відстані семи одиничних відрізків від точки 3. Рухаючись у здовж координатної прямої на сім одиничних відрізків в додатному, а потім у від’ємному напрямах, знаходимо розв’язки х=-4 або х=10.

-4    3    10

0      х

Виконання тесту на комп’ютері.

3. Способи розв’язування рівнянь.

• Презентація групи.
  • розкриття модуля за означенням.

За означенням модуля маємо:

Рівняння для а≥0 рівносильне сукупності рівнянь:

Якщо а<0, то рівняння не має розв’язків.

Приклад : Розв’яжіть рівняння:

Розв’язання

Оскільки 5>0, то рівняння рівносильне сукупності рівнянь:

 Відповідь.   3;-2

Рівняння виду

Рівняння цього виду рівносильне сукупності двох систем: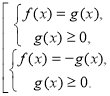
 

Приклад Розв’яжіть рівняння: Iх² +3х-10I=3х-1

 Розв’язання

Рівняння рівносильне сукупності двох систем  Відповідь:3;-3+2√5

• піднесення обох частин до квадрату.

Рівняння виду рівносильне сукупності двох рівнянь:

Приклад. Розв’яжемо рівняння:

 Розв’язання

Рівняння рівносильне сукупності двох рівнянь

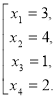
 Відповідь. 1;2;3;4.

Рівняння виду можна розв’язувати піднесенням обох частин рівняння до квадрату.

Приклад , , , , Відповідь. 0;2/3.

• метод інтервалів.

1. Знаходять нулі виразів, що стоять під знаком модуля;
2. Знайдені значення відкладають на числовій прямій, вони розбивають числову пряму на інтервали;
3. Розкривають знаки модулів на кожному з інтервалів.

Приклад. Розв’яжіть рівняння.

Розв’язання

Для цього рівняння на числову пряму наносимо точки х=1та х=2

1  2       х

Ці точки розбивають пряму на 3 інтервали. Розв’язуємо рівняння на кожному з них.

Якщо ,то , , ,. Але число 1 не належить інтервалу . Тому на інтервалі рівняння розв’язків не має.

Якщо , то   Отже, усі є розв’язками рівняння. Якщо то

Оскільки , то - розв’язок рівняння.

Графічний спосіб

Зручно використовувати до рівнянь виду: ,  , та систем. Корені рівняння можна наближено визначити, побудувати графіки функцій та знайшовши абсциси точок перетину їх.

 

• Самостійна робота.

Розв’яжіть рівняння.

а)

б)

в)

г)

4. Рівняння що містять модулі і параметри.

 Серед основних способів розв’язування задач з параметрами є такі:

1. графічний;
2. аналітичний;
3. графічно-аналітичний.

Переваги надають графічному та графічно-аналітичному способам, оскільки вони простіші.

 Приклад. Знайти максимальну кількість розв’язків рівняння.

 .

Розв’язання

За допомогою комп’ютера будуємо графіки функцій:

  ( стаціонарний графік),
(рухомий графік).

Знаходимо найбільшу кількість їх спільних точок, а саме 4, яка відповідає максимальній кількості розв’язків.

 

Технологічна картка 1.

1. Завантажте програму GRAN 1.
2. Завантажте графік функції .

( Меню-Файл-Відкрити F1).

3. Перед початком роботи з новим об’єктом не забудьте вилучити попередній (виділіть функцію та натисніть Delete).

 

Приклад 2. Скільки розв’язків залежно від значення параметра має рівняння

Розв’язання

Подамо рівняння у вигляді  За допомогою комп’ютера  будуємо графіки функцій:

  ( стаціонарний графік)  

( рухомий графік).

За кількістю спільних точок графіків (n) робимо висновок про кількість розв’язків рівняння:

1. якщо , тобто а<-3, то n=0 і розв’язків немає;
2. якщо , тобто а=-3, то n=4 і рівняння має 4 розв’язки ;
3. якщо, тобто 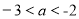, то n=8 і рівняння має 8 розв’язків;
4. якщо, тобто , то n=6 і рівняння має 6 розв’язків;
5. якщо, тобто 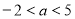, то n=4 і рівняння має 4 розв’язки;
6. якщо, тобто , то n=3 і рівняння має 3 розв’язки;
7. якщо 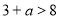, тобто, то n=2 і рівняння має 2 розв’язки.
   Технологічна картка 2.

1. Побудуйте графіки функцій

та

для , , , , ,.

2. Для кожної функції задайте межі відрізка:

А=-7, В=7.

3. Перед початком роботи з новим об’єктом не забудьте вилучити попередній (виділіть функцію та натисніть Delete).

 

Приклад 3.

Скільки розв’язків має система рівнянь

Залежно від значень параметра?

Розв’язання

Будуємо рухомий графік функції

(множина прямих, що мають кутовий коефіцієнт а-3 і проходять через точку (-2;-1) ).

Будуємо графік рівняння (квадрат зі стороною 2, центр якого знаходиться в точці (0;0), а сторони паралельні осям координат).

За кількістю точок  перетину графіків робимо висновок про кількість розв’язків системи:

1. якщо 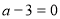, тобто 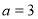, то система має безліч розв’язків;
2. якщо 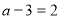, тобто , то система має один розв’язок;
3. якщо , то система має 2 розв’язки;
4. якщо або , то розв’язків не має.

Технологічна картка 3.

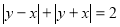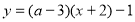1. Побудуйте графіки функцій та для , , , .

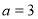Зверніть увагу, що перша функція задана неявно, а всі інші – явно.

2. Для кожної функції задайте межі А=-3, В=3.
3.               Для якіснішого відображення графіків задайте однаковий масштаб на осях (Графік – Властивості - ху).
   Самостійна робота
   Скільки розв’язків має система залежно від значень параметра?

 

 Учні самостійно виконують завдання та контролюють правильність побудов на екрані ПК, порівнюючи їх із попередньо розданим друкованим зразком. Це дозволяє учням з недостатньо сформованими навичками роботи з комп’ютером не відставати від решти учнів класу. На етапі виконання побудови графіків відповідних функцій учні можуть скористатися допомогою консультантів.

 V Рефлексія

VI  Домашнє завдання

1. Знайти розв’язки рівняння

 

залежно від значень параметра.

2. Знайти значення а для яких система

має чотири розв’язки.

 Зауваження. Враховуючи те, що учні не робили малюнків до завдань у зошитах, а тільки записували розв’язання до них, у кінці уроку кожному учневі роздається аркуш з комп’ютерними роздруківками до виконаних завдань, який вклеюється в робочий зошит.

VII Підсумки навчальної діяльності.

 

•                                                                       - Що ви вивчали на сьогоднішньому уроці?
•                                                                       - Що було незрозумілим на уроці?
•                                                                       - Що вам давалось найважче?

 

VIII  Самооцінка учнів. Оцінювання.