Відкритий урок з геометрії в 9 класі "Перетворення фігур"

Комунальний заклад

«Полтавська загальноосвітня школа І-ІІІ ступенів №27

Полтавської міської ради Полтавської області»

 

 

 

 

 

 

Розробка відкритого уроку у 9 класі

 

«Перетворення фігур»

 

 

 

 

 

 

 

 

 

 

 

 

З досвіду роботи

вчителя математики

Комунального закладу

                                                                  «Полтавська загальноосвітня

                                                               школа І-ІІІ ступенів №27

                                                             Полтавської міської ради

                                                       Полтавської області»

                                                                       Гусєвої Л.С.,вчитель

вищої кваліфікаційної

                                                                      категорії,педагогічне звання

« учитель-методист»

 

 

 

                                                         2018 –2019 н.р.

 

Гусєва Л.С.

Комунальний заклад « Полтавська загальноосвітня школа І-ІІІ ступенів №27

Полтавської міської ради полтавської області»,

учитель математики вищої кваліфікаційної  категорії,

педагогічне звання « учитель-методист»

 

 

Перетворення фігур.

Симетрія, види симетрії  (9 клас)

Підсумковий урок (два уроки)

 

Мета: систематизувати знання учнів з теми «Перетворення фігур», повторити відомі види перетворень, їх властивості, класифікувати види симетрій по Вейлю, розвивати кмітливість, допитливість , виховувати почуття прекрасного, домогтися, щоб діти зрозуміли, що поняття симетрії є одним із основних понять будови всесвіту, неорганічного і органічного світу.

 

 

Х І Д    У Р О К У

І. Актуалізація опорних знань і умінь учнів.

Вчитель: ми  вивчали тему „Перетворення фігур”. Поясніть, що ж називають перетворенням однієї фігури в іншу?

Учень: якщо кожну точку даної фігури F змістили яким-небудь чином, і дістали нову фігуру F¹, то говорять, що ця фігура F¹  утворилась перетворенням даної фігури F.

Вчитель: які види перетворень вивчають у школі?

Учень:  вивчають два види перетворень: рух і перетворення подібності.

Вчитель: яке перетворення однієї фігури в іншу називають рухом?

Учень: перетворення однієї фігури в іншу називається рухом, якщо воно зберігає відстань між точками, тобто будь-які дві точки Х і У фігури F переводить у дві точки Х¹ і У¹ фігури F¹ і при цьому ХУ=Х¹У¹.

Вчитель: яке перетворення однієї фігури в іншу називають перетворенням подібності?

Учень: перетворення фігури F у фігуру F¹ називається перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну і ту ж саму кількість разів, тобто це означає, що Х¹У¹=kХУ, де k – коефіцієнт подібності.

Вчитель: перелічіть властивості руху.

Учень:   1) прямі переходять у прямі, промені у промені, відрізки у відрізки.

2) зберігається порядок взаємного розміщення точок на прямій.

3) зберігається градусна міра кутів.

4) зберігається паралельність прямих.

Вчитель: чи є ці властивості характерні для перетворення подібності?

Учень: так. Всі перелічені властивості є характерні і для перетворення подібності.

Вчитель: а, що ж відрізняє ці два види перетворень?

Учень: при рухові одержуємо рівні фігури, а при перетворення подібності – подібні.

Вчитель: які види перетворень відносяться до руху. Перелічіть.

Учень:   а) центральна симетрія;

б) осьова симетрія;

в) поворот;

г) паралельне перетворення.

Вчитель: яке перетворення називають центральною симетрією? Як виконується центральна симетрія? Перелічити  властивості. Довести, що центральна симетрія є рух.

Учень: Перетворення фігури F у фігуру F¹, при якому кожна її точка Х переходить у точку Х¹, симетричну відносно даної точки О, називається перетворенням симетрії відносно точки О або центральною симетрією з центром О.

                  Властивості:

 

                   __________________

 

1. всі три точки Х,О,Х¹ лежать на одній прямій;
2. ХО=ОХ¹.  

 

Теорема: Перетворення симетрії відносно точки є рухом.

Доведення. Нехай Х і У – дві довільні точки фігури F. Перетворення симетрії відносно точки О переводить їх у точки Х¹ і У¹. Розглянемо ХОУ і   Х¹ОУ¹.

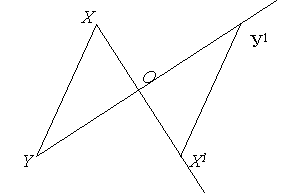Ці трикутники рівні за І ознакою рівності трикутників. У них кути при вершині О рівні як вертикальні, а ОХ=ОХ¹, ОУ=ОУ¹ за властивостями симетрії відносно точки О. З рівності трикутників випливає рівність сторін ХУ=Х¹У¹. А це означає, що симетрія відносно точки О є рух. Теорему доведено.

 

 

 

Вчитель: яке перетворення називається осьовою симетрією? Як виконується осьова симетрія? Властивості. Довести, що осьова симетрія є рух.

Учень: Перетворення фігури F у фігуру F¹, при якому кожна її точка Х переходить у точку Х¹, симетричну відносно даної прямої l, називається перетворення симетрії відносно прямої l.

 

Властивості:

 

 

1) всі три точки Х,О, Х¹ лежать на одній прямій;

2) ХО=ОХ¹.

3) ХХ¹ перпендикулярний l

 

 

Теорема: Перетворення симетрії відносно прямої є рух.

Доведення. Приймемо дану l за вісь ОУ. Візьмемо дві довільні точки А(х₁; у₁) В (х₂; у₂).

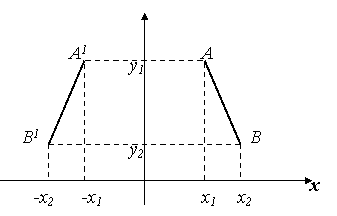Побудуємо симетричні їм точки відносно осі ОУ, одержимо точку А¹(-х₁; у₁) і В¹(-х₂; у₂).

Маємо

АВ²=(х₂-х₁)²+(у₂-у₁)²

А¹В¹=(-х₂+х₁)²+(у₂-у₁)².

Очевидно, що АВ=А¹В^1. Це означає, що перетворення симетрії відносно прямої є рух. Теорему доведено.

 

 

Вчитель: що можна сказати про координати двох точок, якщо вони симетричні: а) відносно початку відліку; б) відносно осі ОХ; в) відносно осі ОУ.

Учень: а) якщо дві точки симетричні відносно початку відліку, то їх координати протилежні А(х; у) А¹(-х; -у); б) якщо дві точки симетричні відносно осі ОХ, то їх абсциси рівні, а ординати протилежні А(х; у) А¹(х¹; -у); в) якщо дві точки симетричні відносно осі ОУ ,то їх абсциси протилежні, а ординати рівні А(х; у) А¹(-х; у).

Вчитель: Діти, вдома ви виконували дві практичні роботи, по центральній і осьовій симетрії, прошу здати їх, за виконання ви одержати оцінки. А тепер перейдемо до усних вправ.

 

Усні вправи.

1. Чи має центр симетрії 1) відрізок; 2) промінь; 3) коло; 4) пара прямих, що перетинаються; 5) пара паралельних прямих. Назвати центр симетрії.

2. Чи може пряма при симетрії відносно даної точки відображатись сама в себе? Чи може промінь при симетрії відносно даної точки відобразитись сам в себе?

3.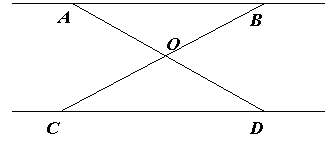 Прямі АВ||СД, точки А і Д симетричні відносно точки О. Пряма ВС проходить через точку О. Довести, що точки В і С – симетричні відносно точки О.

4. Знайти точку Д¹, симетричну точці Д(-5; -7) відносно початку координат? Відносно прямої ОХ? Відносно прямої ОУ?

5. Серед точок А(3; -4), В(-3; -4), С(-3; 4), Д(4; -7), К(-4; 7), Р(3; 4) вказати пари симетричних відносно точки О.

6. Чи симетричні точки М(-5; 8), N(-3; 4) відносно точки К(-1; 2).

7. Знайти центр симетрії точок А(-4; 3) і В(2; -7).

8. Знайти точку С, яка симетрична точці В(-3; 1) відносно точки А(2; -5).

9. Точки А(-4; m) і В(n; 3) симетричні відносно точки К(5; -2). Знайти m і n.

10. Записати рівняння кола, яке симетричне колу (х-4)²+(у+3)²=11 відносно а) початку відліку; б) відносно осі ОХ; в) відносно осі ОУ; г) відносно точки     М(-4; 2).

11. Точки А(х; -2) і В(3; у) симетричні відносно осі ОУ. Знайти х і у.

 

ІІ. Самостійна робота. Учні виконують самостійну роботу по заздалегідь  заготовлених текстах

	І варіант	ІІ варіант
1.	Знайти точку, симетричну даній відносно початку відліку
	А(-3; -4)	В(-5; 8)
2.	Знайти точку, симетричну даній точці відносно осі ОХ
	А(-2; 3)	В(3; -4)
3.	Знайти точку, симетричну даній точці відносно осі ОУ
	А(5; -6)	В(-2; -4)
4.	Знайти центр симетрії двох точок
	А(-6; 4), В(8; -2)	А(3; -4), В(-7; 2)
5.	Знайти координати точки В, симетричної точці А відносно точки О, якщо
	А(1; -5), О(-2; 3)	А(-6; 4), О(1; -2)
6.	Записати рівняння кола, центр якого симетричний центру даного кола відносно початку координат і радіус удвічі більший від радіуса даного кола.
	(х+1)2+(у-4)2=4	(х-4)2+(у+5)2=9
7.	Дано АВС, де А(0; 2), В (-2; 6), С(2; 6). Знайти координати АВ1С1, симетричного даному відносно точки А.	7.	Дано АВС А(-2; 1), В(-1; 5),      С(-6; +2). Знайти координати         А1ВС1, симетричного даному відносно точки В.

На звороті дошки заздалегідь заготовлені правильні відповіді, діти обмінюються варіантами і перевіряють самостійну роботу, а потім оголошуються оцінки.

 

ІІІ. Вчитель. А тепер давайте заслухаємо ті повідомлення, які приготували діти.

Щоб вияснити питання, що ж таке симетрія,

згадаємо старовинну притчу про буріданового віслюка.

У одного філософа по імені Бурідан був віслюк. Одного разу, від’їжджаючи надовго, філософ положив перед віслюком дві однакові кучі сіна – одну зліва, а другу справа. Віслюк не зміг вирішити, з якої почати їсти і здох з голоду. Звичайно, це жарт. Але коли ми поглянемо на малюнок , де зображені дві чаші терезів, то побачимо,

що в обох випадках ліва і права частина настільки однакові, що важко чомусь віддати перевагу.

В обох випадках ми маємо справу з симетрією, яка проявляється в повній рівновазі лівого і правого.                                     

Відомий математики Герман Вейль писав, що „симетрія є тією ідеєю, завдяки якій людина на протязі багатьох віків намагається досягти і створити порядок, красу і цілковиту гармонію». Математично строге означення симетрії сформувалось порівняно недавно в ХІХ ст. В праці „Симетрії” того ж самого Вейля читаємо, що „симетричним називається такий об’єкт, який можна якимось чином змінювати, переміщати, одержуючи в результаті те, що мали спочатку”. Виходячи з цього, необхідно переглянути ті твердження, про які ми говорили раніше. Ми говорили, що існують такі види руху: центральна симетрія, осьова симетрія, поворот, паралельне перенесення. Насправді, по Вейлю, це все одне перетворення – симетрія, а точніше її різні види. Симетрія буває: 1) дзеркальна; 2) поворотна; 3) переносна (трансляційна).

 

 

 

 

 

Розглянемо дзеркальну симетрію. Можливі три випадки: а) якщо об’єкт одномірний, то одержимо центральну симетрію; б) якщо об’єкт двохмірний, то одержимо осьову симетрію; в) якщо трьохмірний, то одержимо симетрію відносно площини. Продемонструємо все сказане на таких малюнках:

 

 

 

                                   

 

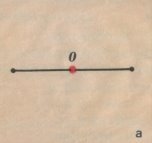
Дзеркальна симетрія по іншому називається геральдичною, тому що використовувалась в зображенні геральдичних гербів. Її можна побачити на відомій срібній вазі царя Ептемени, який правив біля 2700 років до н.е. в країні шумерів, потім на пізніших зображеннях древніх персів, сірійців, візантійців.

 

                    

На Заході дзеркально-симетричні зображення можна побачити на мозаїках кафедральних соборів, храмів, нагробних плитах, іконах, сосудах та інших пам’ятках древнього мистецтва, архітектури.

 

 

                 

 

 

 

 

Наступний вид симетрії – поворотна. Розглянемо букву И. Вона не має дзеркальної симетрії, але якщо повернути її на 180⁰ навколо осі, то буква суміщається сама в себе, тобто буква „И” симетрична відносно повороту на 180⁰. Поворотна симетрія допустима і до букви Ф. Говорять, що якщо об’єкт суміщається сам з собою при повороті навколо деякої осі на кут 360⁰/n, то говорять про поворотну симетрію n^го порядку. Якщо букви N і Ф повертались на 180⁰, то це симетрія 2^го порядку. Квадрат суміщається сам у себе через 90⁰, отже це поворотна симетрія 4^го порядку, у правильного трикутника через 120⁰, тобто 3^го порядку і т.д.

         Розглянемо наступний вид симетрії – переносну (або трансляційну), по суті це той вид перетворень, який ми називаємо паралельним перенесенням. Щоб зрозуміти як виконується переносно симетрія, познайомимось з теорією бордюрів. Бордюр – це малюнок на довгій стрічці, що періодично повторюється. Це може бути орнамент, що прикрашає стіни, галереї, чавунні візерунки на литих  парканах, решітках, на гіпсових барельєфах, керамічних виробах. Всього існує 7 типів бордюрів.

Розглянемо деякі.

1 тип. Самий простий. Схема його така. Один і той самий об’єкт зміщується на один і той самий напрямлений відрізок (вектор).

2 тип. Щоб одержати другий тип бордюра треба взяти окремий об’єкт, відобразити його відносно прямої (осьова симетрія), а потім змістити паралельним перенесенням і т.д.

5 тип. Спочатку виконуємо центральну симетрію даного об’єкта, а потім паралельне перенесення і т.д.

Теорія бордюрів дуже добре ілюструє властивості руху, які стверджують, що 1) два рухи, виконані послідовно, є рухом; 2) перетворення, обернене до руху, є рухом. Говорячи, про бордюри не можна не згадати і орнаменти – ці чудові малюнки,

які часто зустрічаються в декоративно-прикладному мистецтві. Виявляється, це також математика! Орнамент – це не що інше, як дуже чудернацьке поєднання переносної, дзеркальної і поворотної симетрії.

Далеко не треба ходити, погляньте на шпалери в кімнаті. Або погляньте на два орнаменти відомого голандського художника Емера. Один з них „Ящірки”, а другий „Птахи, що летять”.

 

 Існують фігури, які мають і дзеркальну, і поворотну симетрію, і переносну, тобто таке перетворення, яке є композицією кількох видів симетрії.

 

       

 

 

             Розглядаючи симетрію, можна чітко прослідкувати зв’язки математики з різними науками. Так, наприклад, симетрія і астрономія. Спостерігаючи хаотичні розсипи зірок на нічному небу, ми розуміємо, що за зовнішнім хаосом сховані симетричні спіральні структури галактики і   планетних систем. Цю симетрію непогано ілюструє фотографія, на якій зображена наша Галактика і Сонячна система. Але ще більше симетрія проявляється в неорганічному світі. Хто з нас не захоплювався сніговою крижиною! Кожна сніжинка – є маленький кристал, форма сніжинки може бути різною, але всі вони мають симетрію – поворотну 6^го порядку, а також дзеркальну. Тісно пов’язані між собою симетрія і кристалографія – наука про кристали. Уявіть собі правильний многогранник з ідеально правильними кутами, ребрами, гранями. Важко уявити, що це симетричне тіло утворилось само собою, його ніхто не шліфував, ніякий чарівник не будував такі правильні споруди, крім природи. У кожного кристала своя закономірність у розміщенні частинок, його будові. Це можна продемонструвати на прикладах, зображених на фото.

             

 

Приклади симетрії видно і на наступному мал., де показано будову молекули ДНК. Молекула складається із величезної кількості ланок, які називаються нуклеотидами. Ці ланки зв’язані в два ланцюги.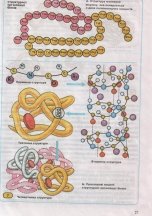 Кожний нуклеотид містить молекулу цукру, фосфорної кислоти, азотистої сполуки. Приведена просторова модель молекули ДНК є не що інше як переносна і поворотна симетрія, де один і той самий набір повторюється нескінчену кількість разів.

Багато прикладів симетрії можна продемонструвати на прикладах живої природи. Дзеркальну симетрію ІІ^го порядку мають листочки, стовбури, деякі квіти. Зірвіть листок дуба, клена, верби і ви впевнитися у цьому. Придивіться до самої скромної польової квіточки – у неї ідеально симетричні пелюстки, при чому це поворотна симетрія 5^го порядку на кут 36⁰.

 

  

 

У тварин поворотна симетрія зустрічається дуже рідко – це у морської зірки і морського їжачка, а в більшості живі істоти мають осьову симетрію. Це пояснюється дією законів природи, і в першу чергу законом всесвітнього тяжіння. Звернемо увагу на стовбур дерева, він завжди є віссю симетрії, завдяки цьому дерево досягає стійкого положення. Така ж осьова симетрія притаманна і самому досконалому витвору природи – організму людини, його фігурі.

 

            

 

Цікава, що чудова дитяча казка Льюїса Керрела „Аліса в Задзеркальї” є не тільки цікавою казкою, а і в деякій мірі серйозною математичною працею, адже її автор, Л.Керрол, сам був математиком і його країна Задзеркальє – є не що інше, як перетворення дзеркальної симетрії ІІІ порядку.

Але ми здивуємо вас іще більше, коли скажемо, що симетрія лежить в основі музичного чи поетичного твору, при чому переносна симетрія, адже в основі музики, поезії лежить ритм – тобто правильне періодичне повторення частки музичного твору, а це і є суть переносної симетрії! А якщо музичний твір записаний нотами на папері – то це очевидне підтвердження такої симетрії. Те ж саме можна сказати і про поетичний твір. Великий німецький поет Йоган Гете говорив, що „всяка музична композиція спирається на скриту симетрію”. Вірші всіх геніальних поетів легко лягають на музику. Поезія і музика – це ніби-то орнамент у часі, сплетений із звуків, нот і слів.

                   

На кінець нашої розмови погляньте на роботи великих майстрів пензля Леонардо да Вінчі „Мадонна Літта” і Рафаєля „Сікстінська мадонна” та інших художників. На цих картинах чітко видно осьову симетрію навіть  неозброєним математикою оком!

 

            

 

 

Таким чином:

1. Ми переконались, що симетрія скрізь, вона оточує нас повсюди, кожна звичайна людина легко помічає її в багатьох проявах. Зате будь-яке порушення симетрії ми сприймаємо з почуттям незадоволення. Ми жалкуємо, дивлячись на птаха з одним крилом, або на криве похилене дерево і думаємо, як могло таке статися! Адже ми знаємо точно, як не повинно бути. Говорячи про симетрію, не можна не сказати про асиметрію.
2. Симетрія і асиметрія поруч, але симетрія це спільна властивість всіх об’єктів оточуючого світу, а асиметрія відображає індивідуальність. Таким чином, симетрія – основа всього, вона первооснова краси.
3. Симетрія – одне із фундаментальних понять, яке лежить в основі неорганічного і органічного світу, в основі будови Всесвіту.

 

І закінчимо урок словами основоположника теорії симетрії Г.Вейля:

 

„Симетрія є тією ідеєю, зо допомогою якої кожна людина на протязі

багатьох віків намагається пізнати і створити порядок, красу і досконалість”