Розв'язки завдань з планіметрії

Варіант 1

Кути паралелограма відносяться як 2 : 3. Знайдіть кут між висотами паралелограма, проведеними з вершини гострого кута.

Розв’язання:

– паралелограм,

Проведемо

(внутрішні різносторонні при AB || CD, січній AD)

(внутрішні різносторонні при AD || BC, січній AB)

;

(внутрішні односторонні при AD || BC, січній AB)

– коефіцієнт пропорційності;

Відповідь: 108°

Варіант 2

Діагональ рівнобічної трапеції ділить навпіл її тупий кут, а середню лінію трапеції на відрізки 4 см і 5 см. Знайдіть периметр трапеції.

Розв’язання:

(внутрішні різносторонні при AD || BC, січній BD)

(BD – бісектриса )

– рівнобедрений, AB = AD = CD

− середня лінія

KN – середня лінія

Відповідь: 38 см

 

 

Варіант 3

Катети прямокутного трикутника дорівнюють 12 см і 16 см. Знайдіть довжину бісектриси трикутника, що проведена з вершини більшого гострого кута.

Розв’язання:

Більший кут трикутника лежить проти більшої сторони. AC = 16, BC = 12, тому .

Проводимо бісектрису BK.

За властивістю бісектриси:

(піфагорова трійка)

  (теорема Піфагора)

Відповідь: см

Варіант 4

Діагональ рівнобічної трапеції перпендикулярна до її бічної сторони. Знайдіть площу трапеції, якщо її основи дорівнюють 12 см і 20 см.

Розв’язання:

ABCD – трапеція, AB = CD, AD || BC,

Для рівнобедреної трапеції , тоді

З прямокутного трикутника ABD:

Відповідь: 128 см²

Варіант 5

Дві сторони трикутника дорівнюють 7 см і 11 см, а медіана, проведена до третьої сторони, на 8 см менша за цю сторону. Знайдіть невідому сторону трикутника.

Розв’язання:

– медіана.

Добудуємо трикутник до паралелограма (продовжимо ВМ за точку М на відрізок MD = BM. Оскільки діагоналі чотирикутника точкою перетину діляться навпіл, то цей чотирикутник паралелограм)

Нехай

Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

;

;

;

; ;

Відповідь: 14 см

Варіант 6

У ромбі висота, що проведена з вершини тупого кута, ді­лить сторону навпіл. Знайдіть площу ромба, якщо його більша діагональ дорівнює см.

Розв’язання:

рівнобедрений (AC = BC).

як сторони ромба. Отже, – рівносторонній,

,

– бісектриса (властивості діагоналей ромба)

Відповідь: см²

Варіант 7

Точка дотику кола, вписаного у прямокутний трикутник, ділить гіпотенузу на відрізки 4 см і 6 см. Знайдіть периметр трикутника.

Розв’язання:

BM = BK = 4, AK = AN = 6, CN = CM = (властивість дотичних, проведених до кола з однієї точки)

(теорема Піфагора)

Відповідь: 24 см

Варіант 8

Сторони трикутника дорівнюють см і 2 см. Знайдіть третю сторону трикутника, якщо вона дорівнює радіусу кола, описаного навколо цього трикутника.

Розв’язання:

За теоремою синусів:

За умовою

За теоремою косинусів:

Відповідь: 1 см

Варіант 9

Сторони трикутника дорівнюють відповідно 11 см, 12 см, 13 см. Знайти медіану, яку проведено до більшої сторони трикутника.

Розв’язання:

Нехай медіана , AC = 13.

Добудуємо трикутник до паралелограма (продовжимо ВМ за точку М на відрізок MD = BM)

Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

;

Відповідь:

Варіант 10

Знайдіть площу прямокутного трикутника, якщо бісек­триса його гострого кута ділить протилежний катет на відрізки завдовжки 3 см і 5 см.

Розв’язання:

AK – бісектриса кута А. За властивістю бісектриси:

(піфагорова трійка)

Відповідь: 24 см²

Варіант 11

Бісектриса кута прямокутника ділить його діагональ у відношені 2:7. Знайдіть площу прямокутника, якщо його периметр дорівнює 108 см.

Розв’язання:

АК – бісектриса кута А прямокутника.

Властивість бісектриси:

– коефіцієнт пропорційності, тоді

Відповідь: 504 см²

Варіант 12

Основи рівнобічної трапеції дорівнюють 6 см і 10 см, а діагональ ділить навпіл тупий кут трапеції. Знайдіть до­вжину цієї діагоналі.

Розв’язання:

(внутрішні різносторонні при AD || BC, січній BD)

(BD – бісектриса )

– рівнобедрений, AB = AD

Проведемо висоту .

 Для рівнобічної трапеції

Відповідь: см

Варіант 13

Бісектриса прямого кута прямокутного трикутника ді­лить гіпотенузу на відрізки завдовжки 15 см і 20 см. Знайдіть радіус кола, вписаного у трикутник.

Розв’язання:

CD – бісектриса прямого кута С.

За властивістю бісектриси:

AB = AD + BD = 20 + 15 = 35

(піфагорова трійка)

BC = 21; AC = 28

Відповідь: 14 см

Варіант 14

Центр кола, описаного навколо  трапеції, лежить на її більшій основі. Знайдіть радіус цього кола, якщо діагональ трапеції дорівнює 20 см, а її висота – 12 см.

Розв’язання:

ABCD – рівнобічна трапеція (оскільки навколо трапеції описано коло), BK – висота, BD – діагональ.

О – центр описаного кола, AD – більша основа трапеції, діаметр описаного кола.

– прямокутний - вписаний кут спирається на діаметр)

(піфагорова трійка)

AD = AK + KD = 9 + 16 = 25

Відповідь: 12,5 см

Варіант 15

Навколо трапеції, основи якої дорівнюють 12 см і 16 см, а висота – 14 см, описано коло. Знайдіть довжину цього кола.

Розв’язання:

ABCD – рівнобічна трапеція (оскільки навколо трапеції описано коло), BK – висота, BD – діагональ.

Коло, описане навколо трапеції співпадає з колом, описаним навколо

Для рівнобічної трапеції:

KD = AD – AK = 16 – 2 = 14

(теорема синусів)

Відповідь: см

Варіант 16

Катети прямокутного трикутника дорівнюють 18 см і 24 см. Знайдіть бісектрису трикутника, проведену з вершини його меншого гострого кута.

Розв’язання:

Менший кут прямокутного тракутника АВС лежіть проти меншого катета ВС. Проведемо бісектрису АК.

(піфагорова трійка)

За властивістю бісектриси:

Відповідь: см

Варіант 17

У трикутнику ABC АМ – медіана. На стороні AB трикут­ника ABC позначили точку K так, що AK : KB = 2 : 3. У якому відношенні медіана АМ ділить відрізок СК?

Розв’язання:

O – точка перетину АМ та СК.

Проведемо через точку К відрізок KF || AM.

ABM: (узагальнена теорема Фалеса)

М – середина ВС (АМ – медіана)

  (узагальнена теорема Фалеса)

Відповідь: 5 : 2

Варіант 18

Перпендикуляр, проведений з точки кола до його радіуса, дорівнює 24 см. Цей перпендикуляр ділить радіус у від­ношенні 5 : 8, починаючи від центра кола. Знайдіть до­вжину кола.

Розв’язання:

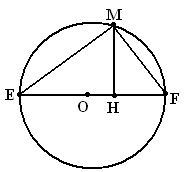Розглянемо коло з центром в точці О. Проведемо з точки М, що лежить на колі .

– коефіцієнт пропорційності,

 

(вписаний кут спирається на діаметр)

Відповідь: см

Варіант 19

У прямокутну трапецію вписано коло, радіус якого до­рівнює 6 см. Точка дотику поділяє більшу бічну сторону трапеції на два відрізки, довжина більшого з яких дорів­нює 8 см. Знайдіть площу трапеції.

Розв’язання:

ABCD – трапеція, BC || AD,

O – центр вписаного кола. CD – більша бічна сторона, М – точка дотику, (радіус, проведений в точку дотику перпендикулярний до дотичної)

Відрізки дотичних, проведених до кола з однієї точки, рівні.

Проведемо радіус ОК. BKON, AKOL – квадрати, сторони яких дорівнюють радіусу вписано кола.

Проведемо висоту CT.

;

BC = BN + CN =   ; AD = AL + LD = 6 + 8 = 14 ;

Відовідь: 133,5 см²

Варіант 20

Знайдіть радіус кола, описаного навколо трапеції, основи якої дорівнюють 11 см і 21 см, а бічна сторона – 13 см.

Розв’язання:

Навколо трапеції можна описати коло тільки якщо вона рівнобічна.

ABCD – трапеція, AD || BC, AB = CD.

Проводимо

Для рівнобічної трапеції

Коло, описане навколо трапеції співпадає з колом, описаним навколо трикутника ABD.

З (піфагорова трійка 5 ; 12; 13);

 (теорема синусів)

Відповідь: см

Варіант 21

Центр кола, описаного навколо трапеції, належить біль­шій основі. Знайдіть кути трапеції, якщо основи відно­сяться як 1 : 2.

Розв’язання:

Навколо трапеції можна описати коло тільки якщо вона рівнобічна. AB = CD,

O – центр описаного кола, середина AD.

AO = OB = OC = OD = R – радіуси кола.

За умовою .

BO = BC = OC - рівносторонній

(за трьома сторонами)

Відповідь: 60°, 120°, 120°, 60°

Варіант 22

Коло, вписане у прямокутну трапецію, ділить точкою до­тику більшу бічну сторону на відрізки завдовжки 4 см і 25 см. Знайдіть площу трапеції.

Розв’язання:

ABCD – прямокутна трапеція, BC || AD,

CD – більша бічна сторона, М – точка дотику, СМ = 4, CD = 25

В трапецію можна вписати коло, тому сума основ дорівнює сумі бічних сторін. AD + BC = AB + CD

DL = DM = 25, CM = CN = 4 (відрізки дотичних, проведених до кола з однієї точки, рівні).

Проводимо висоту CT. TD = LD – LT = MD – CM = 25 – 4 =21

Відповідь: 490 см²

Варіант 23

Бісектриса гострого кута паралелограма ділить його сто­рону у відношенні 3 : 4, рахуючи від вершини тупого кута. Периметр паралелограма дорівнює 80 см. Знайдіть його сторони.

Розв’язання:

ABCD – паралелограм, A < 90°, AK – бісектриса

KAD = AKB (внутрішні різносторонні при  AD || BC і січній АК)

KAВ = AKB (АК – бісектриса)

KAВ = AKB – рівнобедрений, АВ = ВК

– коефіцієнт пропорційності,

Відповідь: 12см, 28см, 12 см, 28 см

Варіант 24

Периметр паралелограма дорівнює 26 см, а його діагона­лі дорівнюють 7 см і 11 см. Знайдіть сторони паралело­грама.

Розв’язання:

Сума квадратів сторін паралелограма дорівнює сумі квадратів діагоналей (наслідок з теореми косинусів).

;

;

;

;

Відповідь: 6 см, 7см, 6 см, 7 см