Урок для учнів 6 класу на тему "Раціональні числа"
Даний матеріал для вчителів, які викладають математику у 6 класі. У даному конспекті є поєднання математики з іншими предметами. До цього матеріалу буде додана презентація та додатковий документ, що містить роздатковий матеріал.
Відділ освіти Тисменицької районної державної адміністрації
Районний методичний кабінет
Угринівський НВК
Раціональні числа.
Ров’язування вправ.
Підготувала
вчитель математики
Угринівського НВК
Стефурак О. М.
Тема: Раціональні числа. Розв’язування вправ.
Мета: навчальна: узагальнити та систематизувати знання учнів з
теми «Раціональні числа»; удосконалити вміння
розв’язувати вправи з цієї теми;
розвивальна: формувати вміння аналізувати та узагальнювати
інформацію;
виховна: виховувати свідоме ставлення до навчання,
відповідальність за результатами своєї роботи.
Тип уроку: узагальнення та вдосконалення знань.
Обладнання та наочність: ноутбук, телевізор, роздатковий
матеріал.
Хід уроку
- Перевірка домашнього завдання за відповідями на екрані.
№1013 (2б): 5; №1059 (1) : 6; -11; ![]() ; -1004;
; -1004; ![]() ;
; ![]() ;
; ![]() .
.
№1067![]() (додатково): х=1, то у=5; х=2, то у=4; х=3, то у=3;
(додатково): х=1, то у=5; х=2, то у=4; х=3, то у=3;
х=4, то у=2; х=5, то у=1.
Питання до учнів «Чи хтось допустив помилку? Яку саме?»
- Організаційний момент. Оголошення теми.
- Математичний диктант.
- Записати за допомогою знаку ‟+„ або ‟-„ висота гори Ай-Петрі 1234 м.
- Записати число розташоване на 5 одиниць вліво від початку відліку.
- Вдень температура повітря була +2⁰С, а на вечір знизилася на 3⁰С. Яка стала температура повітря?
- Дано числа: -5, 4, 0, -2, -3. Вибрати невід’ємні числа і записати.
- До числа 7 записати протилежне.
- Знайти відстань між числами -6 і 6.
- Записати за допомогою знаку ‟+„ або ‟-„ найбільша глибина Білого моря 350 м.
- Модуль числа -13 буде число.
- Порівняйте -5 і -6
-
Знайти корені рівняння
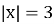
-
Скільки коренів має рівняння
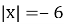 ?
?
- Серед чисел -200, -100, -3, 4 назвати найбільше число.
Взаємоперевірка. Правильні відповіді на екрані.
(Відповіді. 1. +1234 7. -350
2. -5 8. 13
3. -1 9. -5![]()
4. 4, 0 10. -3, 3
5. -7 11. жодного
6. 12 12. 4
При перевірці математичного диктанту звучать питання, що стосуються даної теми. Отже, виконуючи математичний диктант ми побачили. Що від’ємні числа зараз часто використовуються. А чи знаєте ви відколи почали застосовувати ці числа, і ким введено сучасні знаки та поняття? Зараз ми це послухаємо.
- Історична довідка.
Додатні і від'ємні числа були відомі китайським вченим приблизно ІІ ст. до н.е. «Математика в дев’яти книгах» - це була енциклопедія знань китайських вчених Х-ІІ ст до н.е. Описано розв'язання 246 задач. У 8 книзі зустрічаються від'ємні числа.
Додатні кількості в китайській математиці назвали «чен», від’ємні — «фу»; їх зображали різними кольорами: «чен» — червоним, «фу» — чорним. Такий спосіб зображення використовувався в Китаї до середини XIII ст., поки Лі Є не запропонував зручніше позначення від’ємних чисел — цифри, що зображали від’ємні числа, перекреслювали рискою навскіс справа наліво.
У Європі довгий час від’ємні числа дуже рідко застосовували, вважаючи їх “хибними”. У XIII–XVI ст. європейці розглядали їх лише в окремих випадках. З відкриттям кубічних рівнянь, від’ємні числа поступово знаходять місце в алгебрі. Тільки в 1629 р. французький математик Альберт Жірар увів їх сучасну інтерпретацію. Ян Відман - німецький математик увів сучасні позначення додатних і від'ємних чисел з допомогою знаків “+” і “-”
- Робота з підручником
Будемо працювати по рівнях.
Середній рівень (4-6 балів)
№ 1090 (2)
-31.4; -12.5; -10; -6.7; 0; 0.08; 9; 45.
Достатній рівень (7-9 балів)
№ 1098 (1)
-12≤х≤4 і -4.5≤х≤8
-4; -3; -2; -1; 0; 1; 2; 3; 4.
Високий рівень (10-12 балів)
№ 1107 (1)
-1.3≤![]() ≤73.8
≤73.8
Х=-73
Додаткова вправа для тих, хто швидше працює № 1108* (усно з поясненням)
- Завдання із ЗНО.
-
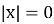 А. 0
А. 0
-
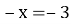
-
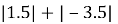 В. 3
В. 3
-
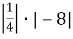 Г. 5
Г. 5
Д. 2
Якщо виписати цифри, які є правильними відповідями попорядку вийде 0352, і оскільки першою цифрою в числі 0 стояти не може, то ми його відкинемо та отримаємо 352. Що це за число?
Ви проживаєте в с.Угринів і ваше село поділене умовно на 2 частини: нижній та верхній Угринів. Чи задавалися ви колись питанням, чому? А тому, що у Верхньому Угриневі є точка, яка знаходиться на висоті 352 м., над рівнем моря, а це є досить високо.
Скажіть за допомогою якого знаку ‟+„ чи ‟-„ будемо записувати дане число?
- Фізкультхвилинка.
- Математичний квест
Ви поділені на 3 групи. На парті перед вами є карточки із завданнями та кольорові карточки із відповідями. Вам потрібно розділити між собою завдання, розв’язати їх та знайти правильну відповідь. Будьте обережні – відповідей є більше. Отже є і неправильні. Знайшовши правильну відповідь підходите до вчительського столу і я по кольору видаю вам слово, яке ви клеїте до дошки. В нас має вийти три речення.
I група
Property and property makes a total of property
(Сума майна і майна є майном)
(Збірник завдань і задач для тематичного оцінювання)
№ 157 (5) (ст.96)
Виберіть серед чисел 863; 6.7; -308; ![]() ; 18; 0; 10; 90.12; -34; -7.2;
; 18; 0; 10; 90.12; -34; -7.2; ![]() цілі від’ємні ( -308; - 34 )
цілі від’ємні ( -308; - 34 )
№ 158 (2)
Знайдіть значення х, якщо –х= - 82 ( 82 )
№ 163 (1)
Знайдіть значення виразу ![]() ( 4.9 )
( 4.9 )
№ 163 (2)
Знайдіть значення виразу ![]() ( 7.54 )
( 7.54 )
№ 163 (4)
Знайдіть значення виразу ![]() (
( ![]() )
)
№ 164 (1)
Обчисліть значення виразу ![]() , якщо
, якщо ![]()
( ![]() )
)
№ 166 (3)
Розв’язати рівняння ![]() ( 0 )
( 0 )
II група
Debt and debt makes a total of debt
(Сума боргу і боргу є боргом)
№ 159 (2)
Знайдіть значення – у, якщо ![]()
№ 163 (3)
Знайдіть значення виразу ![]() ( 5.8 )
( 5.8 )
№ 164 (2)
Обчисліть значення виразу ![]() , якщо
, якщо ![]()
( ![]()
№ 166 (1)
Розв’язати рівняння ![]() (11. -11)
(11. -11)
№ 168 (2)
Порівняйте числа ![]()
![]()
№ 174 (2)
Знайдіть найбільше ціле число, при якому є правильна нерівність
![]()
№ 163 (5)
Знайдіть значення виразу ![]() ( 70 )
( 70 )
III група
Property and debt makes a total of their
(Сума майна і боргу дорівнює їх різниці)
№ 157 (1) (ст.72)
Виберіть серед чисел 863; 6.7; -308; ![]() ; 18; 0; 10; 90.12; -34; -7.2;
; 18; 0; 10; 90.12; -34; -7.2; ![]() натуральні ( 863; 18; 10 )
натуральні ( 863; 18; 10 )
№ 158 (3)
Знайдіть значення с, якщо –с= - 12 ( 12 )
№ 163 (2)
Знайдіть значення виразу ![]() ( 12.1 )
( 12.1 )
№ 163 (3)
Знайдіть значення виразу ![]() ( 22.94 )
( 22.94 )
№ 166 (3)
Розв’язати рівняння ![]() (розв’язків немає)
(розв’язків немає)
№ 164 (1)
Обчисліть значення виразу ![]() , якщо
, якщо ![]()
(![]() )
)
№ 174 (1)
Знайдіть найменше ціле число, при якому є правильна нерівність
![]()
Індійський математик Брахмагупта (VII ст.) використовував такі правила для додавання додатніх і від’ємних чисел. І цю тему ми будемо вивчати на наступних уроках.
- Підсумок уроку
- Що ми з вами сьогодні повторили?
- Що ви дізналися нового?
- Чи сподобався наш урок?
- З якими іншими предметами був взаємозв’язок?
Якщо залишиться часу, то завдання з підручника № 130.
- Домашнє завдання
Повторити §§ 21 – 25
№ 1104; № 1109* (1) додатково.
Історична довідка
Додатні і від'ємні числа були відомі китайським вченим приблизно ІІ ст. до н.е. «Математика в дев’яти книгах» - це була енциклопедія знань китайських вчених Х-ІІ ст до н.е. Описано розв'язання 246 задач. У 8 книзі зустрічаються від'ємні числа.
Додатні кількості в китайській математиці назвали «чен», від’ємні — «фу»; їх зображали різними кольорами: «чен» — червоним, «фу» — чорним. Такий спосіб зображення використовувався в Китаї до середини XIII ст., поки Лі Є не запропонував зручніше позначення від’ємних чисел — цифри, що зображали від’ємні числа, перекреслювали рискою навскіс справа наліво.
У Європі довгий час від’ємні числа дуже рідко застосовували, вважаючи їх “хибними”. У XIII–XVI ст. європейці розглядали їх лише в окремих випадках. З відкриттям кубічних рівнянь, від’ємні числа поступово знаходять місце в алгебрі. Тільки в 1629 р. французький математик Альберт Жірар увів їх сучасну інтерпретацію. Ян Відман - німецький математик увів сучасні позначення додатних і від'ємних чисел з допомогою знаків “+” і “-”
Роздатковий матеріал



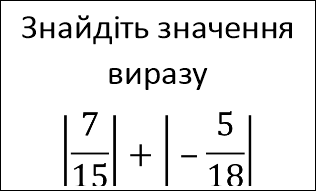

















1


про публікацію авторської розробки
Додати розробку
