Урок з математики, 6кл. за темою: "Довжина кола"

Розробка уроку з математики, 6 кл.   Вчитель: Ганенко Вікторія Леонідівна

Тема: Довжина кола

Мета: Ознайомити учнів з поняттям «довжина кола», та навчити знаходити довжину кола. Показати практичне застосування формули довжини кола для розв’язування практичних задач. Розвивати уяву, пам'ять, логічне мислення. Виховувати позитивне ставлення до навчання та зацікавленість предметом математики.

Обладнання: проектор, слайди, обруч, моделі кола, нитка, лінійка, монета.

Тип уроку: вивчення нового матеріалу.

Хід уроку:

1. Організаційний момент.

«Знати – це означає, насамперед, уміти користуватися знаннями».

В.О. Сухомлинський.

2. Перевірка домашнього завдання.

Усно звірити отримані результати.

3. Актуалізація опорних знань.

На дошці причеплено гімнастичний обруч (хулахуп). Учням пропонується розглянути його і відповісти на запитання:

• На яку фігуру він схожий? (коло)
• Як називається точка всередині нього? (центр кола)
• Яка відстань від центра до точки кола? (виміряти лінійкою)
• Як вона називається? (радіус)
• Яка довжина діаметра? (радіус помножений на 2)
• Як називається частина кола? (дуга)
• Як називається дуга, що є половиною кола? (півколо)

4. Мотивація навчальної діяльності.

Проблемне питання:

Чи читали ви роман Жюля Верна «Навколо світу за 80 днів»? Один з героїв цього роману задався питанням: Як рухалися частини його тіла під час навколосвітньої подорожі, голова, чи ноги подолали більший шлях, а можливо порівну? Тема сьогоднішнього уроку допоможе нам знайти відповідь на ці запитання. Сьогодні ми вивчаємо довжину кола.

5. Вивчення нового матеріалу.

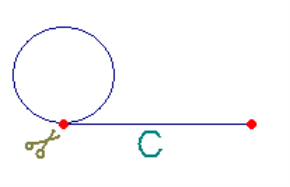
Якщо ми візьмемо кільце з паперу та розріжемо це коло, то довжина цієї полоси є довжиною кола. Її позначають літерою С.

Практична робота:

Для виконання наступного досліду нам потрібні: нитка, лінійка та монети 5 коп. і 50 коп. Виконаємо наступні вимірювання та заповнимо таблицю:

А) діаметр кожної монети вимірюємо лінійкою;

Б) довжину кола кожної монети вимірюємо ниткою.

В) Порівняємо відношення довжини кола до діаметра обох монет

Висновок: Відношення довжини кола до його діаметра завжди стала величина.

Це вперше відмітив ще Архімед (.287-212 рр. до н.е.). Але тільки у 1736 р. Леонардо Ейлер ввів позначення для цього числа і його найбільш точне значення.

Ми для розв’язання задач беремо округлене значення числа Пі до сотих.

В Сіетлі (США) існує пам’ятник числу П, який знаходиться на сходах перед Музеєм мистецтв.

 Через те що відношення довжини кола до його діаметра завжди стала величина – число Пі, можна вивести формулу знаходження довжини кола:

    або    

6. Фізкультхвилинка

Зараз ми всі разом встали.

Швидко руки вверх підняли,

В сторони, вперед, назад.

Повернулись вліво, вправо,

Тихо сіли, знов за справи.

7. Відпрацювання вмінь та навичок.

№1. Давайте знайдемо довжину екватора землі, якщо радіус Землі приблизно 6370 км. (С=2 π r.С≈2*3,14*6370≈40003,6 км)

№2. На цирковій арені кінь побігає коло за 3 хв. Зі швидкістю 13,5 м/хв. Який діаметр арени?(С=V*t=13,5*3=40,5(м) – довжина кола арени. d= C/π=40.5/3.14≈13(м))

8. Підсумки уроку.

Повернемось до задачі Жюля Верна. Знайдемо, який шлях пройшли ноги, та який шлях «пройшла» голова, якщо радіус Землі приблизно 6370 км., а зріст людини приблизно 2 м. = 0,002 км.

Розв’язання: 

1. =2*3,14*6370 = 40003,6 (км)
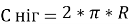
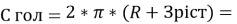2. 2*3,14*(6370+0,002) = 40003,612 (км)
3. 40003,612 – 40003,6= 0,012 (км) = 12 м

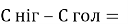
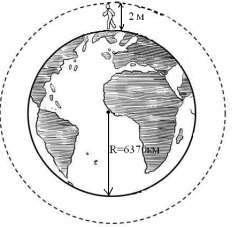Відповідь: За час навколосвітньої подорожі голова подолала на 12 м. довший шлях ніж ноги. 

Ось таке незвичне застосування цієї теми! Чи сподобалась вам тема? Що запам’ятали з уроку?

Домашнє завдання:

Хвилинна стрілка годинника за 15 хв. проходить відстань 6,28 см. Знайди довжину стрілки годинника.