Урок-дослідження "Площа паралелограма"

Тема:  Площа паралелограма

Мета: Навчальна. Вивести формулу для знаходження площі паралелограма, формувати навички розв’язування задач із використанням отриманої формули.

Розвиваюча. Розвивати логічне мислення, пам’ять, кругозір учнів, вміння працювати в групі.

Виховна. Виховувати цікавість, допитливість.

Тип уроку: формування нових знань, умінь та навичок.

Вид уроку: дослідницька робота.

Обладнання: паперові моделі паралелограмів, ножиці, маркери.

Види роботи: групова робота, колективна робота.

Хід уроку:

І. Організаційний момент

ІІ. Актуалізація опорних знань учнів

Запитання до класу:

1. Що таке рівновеликі фігури?
2. Властивості площі фігури:

1. рівні фігури мають….
2. якщо дану фігуру розбити на частини, то площа даної фігури буде дорівнювати….

3.  Що таке палетка?
4. Як визначають площу фігури за допомогою палетки?

ІІІ. Мотивація навчальної діяльності. Проблематизація.

Як, використовуючи формулу площі прямокутника і властивості площі фігури, знайти площу паралелограма?

(Якщо дану фігуру розбито на частини, які є геометричними фігурами, то площа даної фігури дорівнює сумі площ одержаних фігур)

ІV. Об’єднання дітей у групи,

Для розв’язання даної проблеми учні об’єднуються у дві групи. Групам роздаються паперові моделі паралелограма зі сторонами а та b і висотою h, ножиці, маркери, папір.

1. Самостійна робота над дослідженням

Розглядаються два варіанти:

                          1 варіант                                                       2 варіант

Вчитель наводить учнів на думку, що з паралелограма можна зробити прямокутник, розбивши його на частини.

                     

2. Створення продукту проектної роботи

Зробивши з паралелограма прямокутник, учні роблять висновок, що площа паралелограма зі стороною а і висотою h, дорівнює площі прямокутника зі сторонами а і  h.

Позначивши в першому варіанті сторону основи а, а висоту – h_a, а в другому варіанті – бічну сторону b, а висоту – h_b, учні роблять висновок, що

S_пар-ма = а h_a

S_пар-ма = b h_b

V. Презентація роботи

Групи по черзі представляють свою роботу біля дошки, використовуючи моделі, з якими вони працювали.

Перша група представляє утворений прямокутник зі сторонами h та а, друга група –  прямокутник зі сторонами h та b.

         Робота першої групи:                                Робота другої групи:

VІ. Спільна робота класу над поставленою задачею

Вчитель: Якщо площу одного паралелограма можна виразити двома способами, використовуючи різні елементи даної фігури (S = а h_a , S  = b h_b), то можна і прирівняти праві частини даних формул.

а h_a  = b h_b

Яка пропорція випливає з даної рівності?

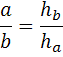
Висновок: Сторони паралелограма обернено пропорційні його відповідним висотам.

VІІ. Аналіз роботи проектних груп та оцінювання роботи учнів.

Запитання до класу

1. Про що нове ви дізналися з уроку?
2. Чи існує паралелограм, сторони якого дорівнюють 4 см і 6 см, а відповідні висоти 5 см і 3 см?
3. Що на уроці було найскладнішим?
4. Які труднощі подолали?

VІІІ. Домашнє завдання