Урок з теми "Подібність трикутників. Підготовка до контрольної роботи"
Предмет: геометрія
Клас: 8
Тема: Подібність трикутників. Підготовка до контрольної роботи.
Мета уроку: узагальнити та систематизувати знання учнів з теми «Подібність трикутників»;
виховати вміння аналізувати, культуру спілкування математичною мовою;
розвити логічне мислення, уміння працювати в групі, робити висновки;
Тип уроку: узагальнення та систематизація знань, умінь і навичок учнів –
урок-презентація.
Форми роботи:
- Взаємоперевірка;
- Бліц-інтерв’ю
- Колективна робота в групах;
- Самоаналіз;
Хід уроку.
І. Організаційний момент.
Учні об’єднуються в групи, кожна з яких складається з учнів з різним рівнем підготовки.
ІІ. Перевірка домашнього завдання
Учні перевіряють розв’язання тесту одне в одного за відповідями, які проектуються на екран.
Відповіді до завдань домашнього тесту:
1. Г. 2. Б. 3. Г. 4. В. 5. В. 6. Б. 7. Г. 8. Г. 9. Б. 10. Г. 11. В. 12. А.
ІІІ. Формулювання теми, мети і завдань уроку
ІV. Актуалізація опорних знань.
Проводиться у формі бліц-інтерв’ю. Група, що дала найбільшу кількість правильних відповідей, заробляє бонус – 1 бал.
Запитання бліц-інтерв’ю
1. ∆МNК ![]() ∆АFC. Що із цього випливає?
∆АFC. Що із цього випливає?
2. Що можна сказати про трикутники, відповідні сторони яких є пропорційними?
3. Два кути трикутника рівні. Що можна сказати про його сторони?
4. Дві сторони трикутника пропорційні. Чи подібні ці трикутники?
5. Яку умову потрібно додати до пункту 4, щоб трикутники були подібними?
6. Які пропорційні відрізки ви можете назвати в прямокутному трикутнику?
7. Чому дорівнює квадрат гіпотенузи в прямокутному трикутнику?
8. Як пов’язані між собою дотична й січна, проведені з однієї точки поза колом до кола?
9. На які відрізки бісектриса кута ділить протилежну йому сторону?
10. Як відносяться висоти подібних трикутників?
11. Чи є правильним твердження, що всі рівнобедрені трикутники подібні?
12. Чи є правильним твердження, що рівнобедрені прямокутні трикутники подібні?
V. Узагальнення набутих навичок і вмінь
Розв’язування різнорівневих задач у групах
Усім групам даються однакові завдання. Консультант групи організує всіх членів групи так, щоб кожний виконав певну частину роботи. Група вважається готовою до презентації розв’язання задач біля дошки за умови, що будь-який член групи може провести презентацію. Група, що виконала завдання раніше відведеного часу, розв’язує додаткову задачу, за правильне розв’язання якої група одержує бонус – 2 бали додатково.
Завдання групам
-
У трикутниках АВС і DEF
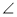 А =
А = 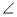 Е,
Е, 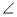 С =
С = 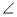 D, СА = 6 м, DE = 10 м, суми сторін АВ і EF, ВС і DF відповідно дорівнюють 24 м і 32 м. Знайдіть довжину цих сторін.
D, СА = 6 м, DE = 10 м, суми сторін АВ і EF, ВС і DF відповідно дорівнюють 24 м і 32 м. Знайдіть довжину цих сторін.
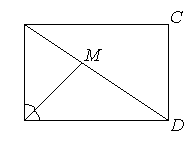
- Бісектриса, проведена з вершини прямокутника, ділить його діагональ на відрізки 15 см і 20 см. Знайдіть периметр прямокутника.
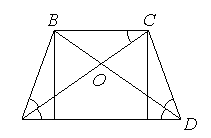
- Дано рівнобедрену трапецію АВСD (ВС || АD), АС, ВD – бісектриси гострих кутів, які перетинаються в точці О. АО : ОС = DO : ОВ = 13 : 5; висота ВЕ = 32 см. Знайдіть периметр трапеції.
Додаткова задача. Діагональ рівнобедреної трапеції ділить висоту, проведену з вершини тупого кута, на відрізки завдовжки 15 см і 12 см, а бічна сторона трапеції дорівнює її меншій основі. Знайдіть сторони трапеції.
(Відповідь: 45 см; 45 см; 45 см; 117 см)
Розв’язання задач 1 – 3.
Задача 1. Розв’язання
Нехай АВ = х м (х > 0), а ВС = у м (у > 0), тоді EF = (24 – х) м, DF = (32 – у) м. Із рівності кутів А і Е, С і D випливає подібність трикутників АВС і EFD. Звідси ![]() ;
; 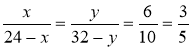 ;
; ![]() ; 5х = 72 – 3х; 8х = 72; х = 9. Отже, АВ = 9 м, FE = 24 – 9 = 15 м.
; 5х = 72 – 3х; 8х = 72; х = 9. Отже, АВ = 9 м, FE = 24 – 9 = 15 м. 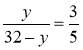 ; 5у = 96 – 3у; 8у = 96; у = 12.
; 5у = 96 – 3у; 8у = 96; у = 12.
Отже, ВС = 12 м, DF = 20 м.
Відповідь: 9 м, 12 м, 15 м, 20 м.
|
Задача 2. Розв’язання
Нехай АВСD – даний прямокутник, ВD – його діагональ. АМ – бісектриса кута А, ВМ = 15 см, МD = 20 см. За властивістю бісектриси в трикутнику ВАD маємо: |
|
|
ВD2 = 25х2; ВD = 5х. З іншого боку, ВD = ВМ + МD = 35 (см).Отже, 5х = 35; х = 7. Звідси АВ = 21 см, АD = 28 см. Отже, РАВСD = 2(АВ + АD) = 2(21 + 28) = 98 (см). Відповідь: 98 см. |
|
|
Задача 3. Розв’язання
Нехай АВСD – дана трапеція. ∆ВОС ∞ ∆АОD, оскільки АО : ОС = DO : ОВ = 13 : 15, |
|
|
й січній АС), тоді
Із трикутника СFD (
РАВСD = 3 · ВС + АD = 3 · 5х + 13х = 28х = 28 ·
Відповідь: 298 |
|
VІ. Підсумки уроку
Технологія «Мікрофон».
Запитання до класу:
- Яка тема уроку?
- Які факти були повторені на початку уроку?
- Які форми роботи були використані на уроці?
- Які учнів працювали активно? Неактивно? Не працювали?
- Який настрій був у вас на уроці й чому?
- На розвиток яких рис характеру вплинув цей урок?
- Що заважало вам працювати продуктивно
- Про що корисне для подальшого навчання ви дізналися на цьому уроці?
- Чим цей урок важливий для вас?
- У яких ситуаціях ви зможете застосувати отриманий досвід?
VІ. Домашнє завдання
- Підготуватися до контрольної роботи з теми «Подібність трикутників».
- Розв’язати задачі.
Середній рівень: Задачі 1, 4 варіанта А на стор. 134 підручника.
Достатній рівень: Задачі 2, 4 варіанта Б на стор. 134 підручника.
Високий рівень: Задача 7 на стор. 137 підручника.


про публікацію авторської розробки
Додати розробку