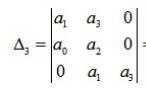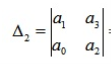Дисципліна: "Основи автоматичного керування та робототехніка»

 

МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ  РОБОТИ

 

«Дослідження стійкості системи автоматичного управління»

 

Мета роботи: дослідити замкнуту систему автоматичного управління (САУ) за допомогою критеріїв стійкості.

 

 

Короткі теоретичні відомості

 

Лінійна система називається стійкою, якщо при виведенні її зовнішніми діями із стану рівноваги (спокою) вона повертається в нього після припинення зовнішніх дій. Якщо після припинення зовнішньої дії система не повертається до стану рівноваги, то вона є нестійкою.  Для нормального функціонування системи управління необхідно, щоб вона була стійкою, оскільки інакше в ній виникають великі помилки.

 Властивість стійкості САУ є важливою властивістю, абсолютно необхідною для забезпечення працездатності системи. Тому дослідження стійкості САУ є важливим елементом теорії автоматичного управління.

 Для визначення стійкості системи автоматики необхідно вирішити диференціальне рівняння, що описує цю систему. Є також спрощені, але достатньо точні методи, які називаються критеріями (умовами) стійкості.

 

Програма лабораторної роботи

 

1.               Реалізувати САУ, структурна схема якої представлена  на рисунку 1, згідно з даними варіанту (див. таблицю 1):

 

Таблиця 1 – Варіанти параметрів ланок

 

Варіант	ko	k1	k2	To	T1
1	10	2	1	0,1	0,56
2	6	2,1	0,8	0,13	0,24
3	3	2,6	1,4	0,16	0,08
4	8,5	1,7	0,4	0,18	0,49
5	9	2,2	1,1	0,12	0,62
6	4	2,0	1,3	0,10	0,22
7	7	2,4	0,9	0,11	0,38
8	5	2,5	0,6	0,15	0,41
9	8	2,3	1,2	0,14	0,64
10	6,5	1,9	0,9	0,17	0,12

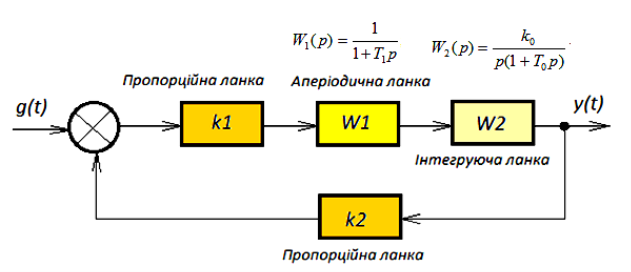
Рисунок 1 - Структурна схема системи

 

 

2.               Перевірити систему на стійкість по вигляду її перехідної характеристики

3. Визначити стійкість системи по критерію Ляпунова.

4. Перевірити систему на стійкість по алгебраїчному  критерію Рауса-Гурвіца.

5. Перевірити систему на стійкість по частотному критерію Михайлова.

6. Перевірити систему на стійкість по частотному критерію Найквіста.

 

 

Порядок виконання лабораторної роботи

 

1.               Математична реалізація передавальних функцій САУ

 

Запишемо передавальні функції ланок САУ, що представлені на рисунку 1, а також передавальні функції розімкнутої та замкнутої  систем в загальному вигляді:

 

       (1)

 

 

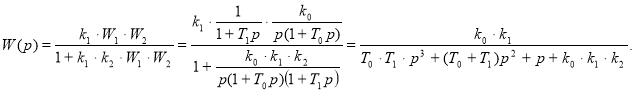(2)

 

 

 

 

2.               Визначення стійкості системи по її перехідній характеристиці

 

 

По вигляду перехідної функції (див. рисунок 2) можна судити про стійкість системи, час перехідного процесу, величину перерегулювання, статичну помилку і інші динамічні характеристики системи. Система буде стійка, якщо її вільні рухи затухають з часом і в системі встановлюється вимушений процес.

 

 

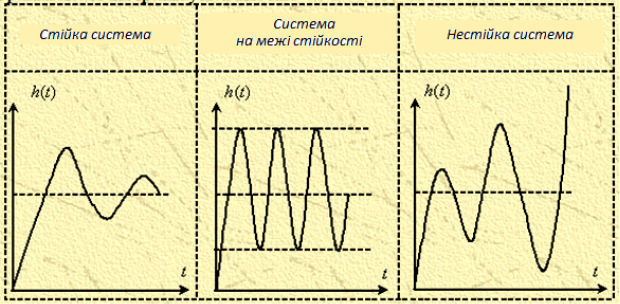
Рисунок 2 – Характер вільних рухів  в САУ

 

Для нестійких систем ця умова не виконується, тоді практичне їх використання є неможливим.

 

Запустіть комп’ютерну програму моделювання автоматичних систем  SamSim і побудуйте у вікні редагування  структурну схему моделі дослідження інтегруючої   ланки з  типових блоків, що представлені у вікні бібліотек програми  (див. рисунок 3). Встановіть контрольні точки на виходах блоків.

 

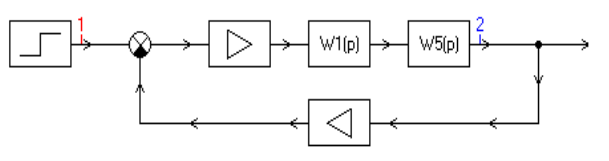
Рисунок 3 – Структурна схема моделі дослідження системи

 

 

Задайте чисельні значення джерела сигналу та   ланкам системи згідно з варіантом.

Виконайте програмний розрахунок схеми (натисніть кнопку «Розрахунок» на панелі інструментів) і у вікні графіків одержіть перехідну характеристику системи при заданих параметрах елементів і вхідній одиничній дії (див. приклад на рисунку 4).

 

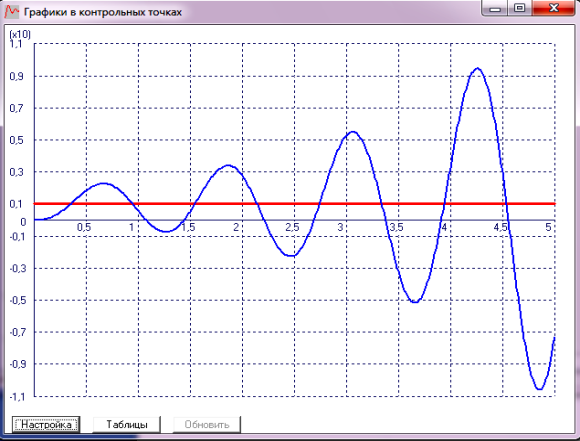
Рисунок 4 – Приклад перехідної характеристики системи

 

Стійкою називається система автоматики, яка після припинення дії збурюючих чинників прагне до початкового або нового стійкого стану, тобто перехідні процеси в ній є затухаючими.

 Порівнюючи   одержану перехідну характеристику з характером вільних рухів САУ (дів. рисунок  2) можна зробити висновок, що  досліджувана система є нестійкою.

 

3.               Визначення стійкості системи по критерію Ляпунова

 

Диференціальне рівняння, яке  описує систему, після перетворення Лапласа, має наступний вигляд

     

,       (3)

 

де g (p) – вхідна дія.

Стійка система повертається в стан спокою, якщо вхідна дія g(p) = 0. Таким чином, для стійкої системи рішення однорідного диференціального рівняння    повинно прагнути до нуля при t, що прагне до нескінченності.

комплексні коріння характеристичного  рівняння.

 Якщо дійсна частина коріння характеристичного рівняння  a_k < 0, то в системі відбуваються затухаючі коливання. При a_k > 0  –  в САУ відбуваються коливання зростаючої амплітуди, а при a_k = 0 - в САУ відбуваються коливання постійної амплітуди.

 

Критерій Ляпунова: для стійкості лінійної автоматичної системи управління необхідне і досить, щоб дійсні частини всіх коренів характеристичного рівняння системи були негативні.

 

 Визначить  корені  заданого характеристичного рівняння замкнутої САУ методом Кардано-Віета за допомогою комп’ютерної програми (калькулятора) Equation Wizard (на рисунку 5 представлений фрагмент вікна, на якому зображений процес визначення коренів):

 

.

 

 

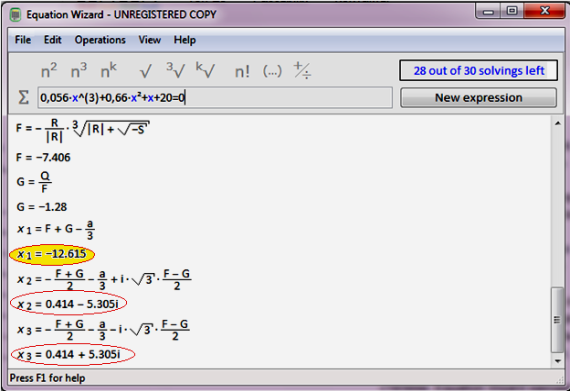
Рисунок 5 - Вікно калькулятора  Equation Wizard

 

В даному прикладі розрахунок показує, що два дійсні кореня характеристичного рівняння мають позитивну дійсну частину, що характеризує систему як нестійку.

 Проте користуватися критерієм Ляпунова на практиці для оцінки стійкості реальних систем достатньо складно, оскільки реальні промислові системи описуються диференціальними рівняннями високого порядку, або містять ланки чистого запізнювання, так що знаходження корінь характеристичного рівняння представляє важке завдання.  Для таких систем застосовуються наступні критерії стійкості: алгебраїчний критерій, Рауса-Гурвіца; частотний критерій Михайлова; амплітудно-фазочастотний критерій Найквіста.

 

 

4.               Перевірка системи на стійкість за критерієм Рауса-Гурвіца

 

 

Одним з найбільш поширених алгебраїчних критеріїв стійкості є критерій стійкості Рауса-Гурвіца. Він заснований на аналізі коефіцієнтів характеристичного полінома. 

Порядок перевірки стійкості САУ  по даному критерію наступний.

З коефіцієнтів характеристичного полінома

 

,

 

вважаючи, що  a_n > 0 , складається головний визначник Гурвіца.

Система стійка, якщо головний визначник Гурвіца і всі визначники нижчого порядку є позитивними.

 Головний визначник Гурвіца має такий загальний вигляд:    

 

 

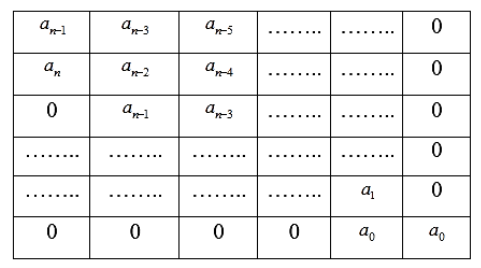
З головного визначника Гурвіца виділяються визначники нижчого порядку (мінори).

 

   і так далі .                                                      

Номер визначника Гурвіца відповідає його розмірності.

 

Критерій Рауса-Гурвіца: для того, щоб лінійна система автоматичного управління була стійка, необхідне і досить, щоб  всі визначники Гурвіца були позитивними, тобто

 

 

Виконайте  розрахунок визначників Гурвіца  в програмі  Exсel за наступним  алгоритмом (приклад):

 

Вхідні дані за варіантом:

 

К0	10
К1	2
К2	1
Т0	0,1
Т1	0,56
	Підстановка заданих даних в характеристичне рівняння  (2)
0,056	p3		+	0,66		P2	+		1		p		+				20			=	0
a0				a1					a2								a3
Виділення мінорів:
0,66	20	0			0,66			20
0,056	1	0			0,056			1
0	0,66	20
D3	-9,2				D2			-0,46				D1			0,66

 

D3 = a1·a2·a3+a3·0·0+0·a0·a1-0·a2·0-a1·0·a1-a3·a0·a3 =  a1·a2·a3 - a3·a0·a3.

D2 = a1·a2 – a0·a3.

 

Розрахунок визначників Гурвіца  показує, що досліджувана система із заданими параметрами є нестійкою, оскільки   два визначники Гурвіца є негативними.

 

5.               Перевірка системи на стійкість по частотному критерію Михайлова

 

 

Як і при використанні критерію Гурвіца початковою інформацією для використання критерію Михайлова є характеристичне рівняння досліджуваної системи. Тут застосовується геометрична ілюстрація траєкторії руху кінця вектора Михайлова - годограф Михайлова.

 На основі характеристичного рівняння замкнутої системи  вводиться в розгляд деяка функція комплексного змінного, яка одержана заміною  оператора p = jω.

 

+          (4)    

                                                      

Функцію (4) можна представити у вигляді

 

   .                                        (5)

 

Підставте в характеристичне рівняння замість оператора р вираз jω і одержіть багаточлен Михайлова для  заданих умов, наприклад:

 

D(jω) = 0,056(jω)³ + 0,66(jω)² + (jω) + 20,

або

 

D(jω) =  –0,056jω³ – 0,66ω² + jω + 20 = (20 – 0,66ω²) + j(ω-0,056ω³ ).

 

Розбийте  багаточлен на  дійсну  і  на уявну частини:

 

Re(ω) = 20 – 0,66ω²,      Im(ω) = ω - 0,056ω³.

Надайте кутовій  частоті  ω  різних значень (від 0 до ∞) і зведіть результати обчислень у таблицю 2:

 

Таблиця 2 – Приклад результатів обчислень багаточлена Михайлова

ω	0	1	2	3	4	5	6	7	8	9	∞
Re(ω)	20	19,34	17,36	14,06	9,44	3,5	-3,76	-12,34	-22,24	-33,46	∞
Im(ω)	0	0,944	1,552	1,488	0,416	-2	-6,096	-12,21	-20,67	-31,82	-∞

За даними таблиці 2  в програмі Excel побудуйте годограф Михайлова в комплексній площині, відкладаючи значення R_e(ω) по дійсній осі, а значення I_m(ω) по уявній осі (див. приклад на рисунку 6).

На комплексній площині R_e-I_m вектор D(jω) буде описувати при зміні  частоти ω от 0 до ∞ криву - годограф Михайлова (див. рисунок 6).

 

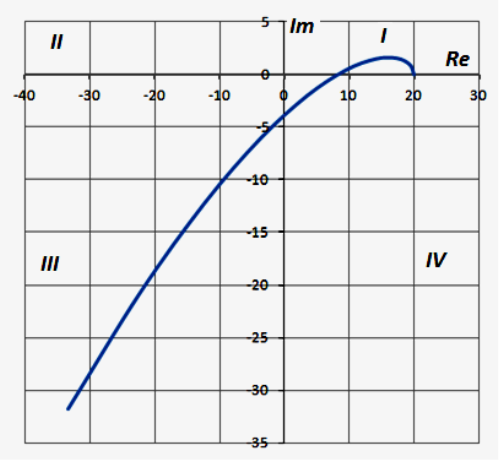
Рисунок 6 – Годограф Михайлова

 

Критерій Михайлова: для стійкої системи управління n-го порядку необхідне і достатнє, щоб годограф Михайлова при зміні  частоти ω від нуля до безкінечності, починаючи з дійсної позитивної піввісі, проходив проти годинникової стрілки послідовно через n- квадрантів.

З побудованого приклада годографа видно, що годограф, обертаючись  проти годинної стрілки на кут 3·π/2 = 270°,  проходить  у перший квадрант,   а потім одразу  у третій (непослідовно) квадрант.

Через те що  критерій Михайлова не виконується,  робимо висновок, що  система, яка  описується заданим характеристичним рівнянням,  нестійка.              

 

 

 

 

 

 

6.               Перевірка системи на стійкість по амплітудно-фазочастотному критерію Найквіста

 

 

Частотний критерій стійкості Найквіста дозволяє судити про стійкість замкнутої системи автоматичного регулювання по її амплітудно-частотній характеристиці в розімкненому стані.

 

  Критерій Найквіста: для того, що б автоматична система, стійка або нейтральна в розімкненому стані, була стійка в замкнутому стані необхідне і достатнє, щоб годограф АФЧХ розімкненої системи не охоплював точку М{-1, j0} на комплексній площині при зміні частоти  ω від нуля до безкінечності і повороті вектора  АФЧХ W(jω) за годинниковою стрілкою (див. приклад на рисунку 7).

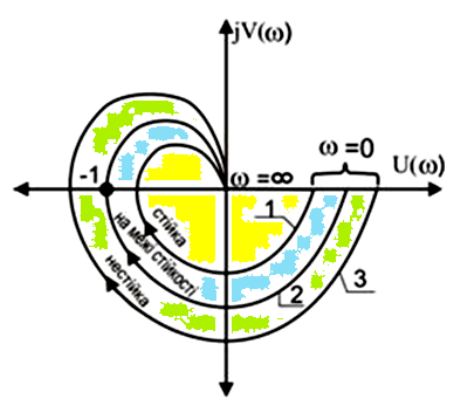
Рисунок 7 – Годограф Найквіста

 

Для побудови частотних характеристик у програмі моделювання автоматичних систем  SamSim  на вході схеми моделювання САУ поставте генератор хитної частоти («ГХЧ»). Частотний діапазон і вид характеристики задаються параметрами вхідного елемента – ГХЧ (див. рисунок 8).

Структурна схема моделі дослідження системи повинна бути розімкненою.

 

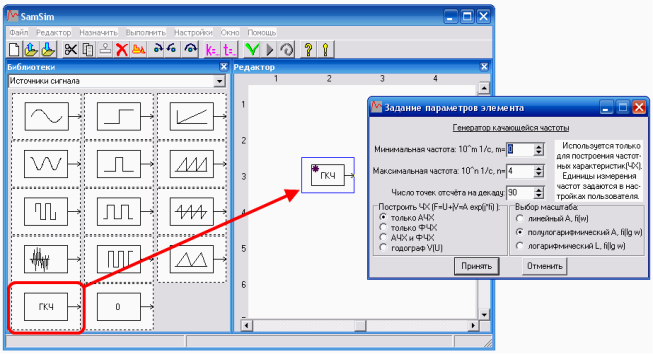
Рисунок 8 – Установка генератора хитної частоти (ГХЧ)

 

Виконайте   програмний розрахунок схеми (натисніть на  кнопку «Розрахунок» на панелі інструментів) і у вікні графіків одержіть годограф Найквіста системи (див. приклад на рисунку 9).

 

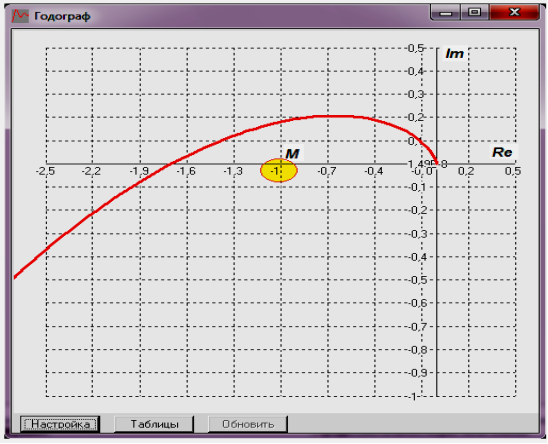
Рисунок 9 – Годограф Найквіста

На рисунку 9 видно, що годограф АФЧХ розімкненої системи охоплює точку М{-1, j0} на комплексній площині при зміні частоти  ω від нуля до нескінченності і повороті вектора  АФЧХ W(jω) за годинниковою стрілкою. Таким чином, досліджувана система є нестійкою.

 

 

 

 

 

 

 

Зміст  звіту лабораторної роботи

 

1.               Назва й ціль лабораторної роботи.
2.               Диференційне рівняння, передавальна та перехідна функції САУ.
3.               Варіант завдання та структурна схема моделі САУ.
4.               Вікно калькулятора  Equation Wizard.
5.               Розрахунок визначників Гурвіца  в програмі  Exсel.
6.               Годограф Михайлова. 
7.               Годограф Найквіста.
8.               Короткі висновки по роботі.
9.               Короткі відповіді на контрольні відповіді.

 

 

Контрольні питання

 

1. Назвіть способи опису динамічних властивостей САУ.

2. Назвіть характерні особливості передавальної функції стійкої САУ.

 

 

Література

 

1.               Головінський Б.Л. Теорія автоматичного управління / Б.Л. Головінський, Ю.В. Шуруб, В.П. Лисенко. - Київ: ВЦ НУБіП України, 2012.
2.               Климентовський Ю.А. Технiчнi засоби автоматики / Ю.А. Климентовський, А.М. Гладкий. – К.: Видавництво «КВIЦ», 2003.
3.               Попович М.Г. Теорія автоматичного керування: підруч. для студ. вищ. техн. навч. закл. / М.Г. Попович, О.В. Ковальчук. – К.: Либідь, 2007.