Урок-досліження: "Площа трапеції"

Олександрівський ліцей

Скадовської  міської ради

Херсонської області

Вчитель: Бульдяк Катерина Василівна

Урок –дослідження

Геометрія 8 клас

Тема : Площа трапеції   
 

Мета: створити умови для усвідомлення та осмислення   
блоку нової навчальної інформації засобами технології проблемного навчання 
та з використанням елементів особистісно-орієнтованого   

навчання ,особистісно-орієнтованого    навчання.   

Завдання:   

• освітні: формування навичок виведення формул для 
обчислення площі многокутників ;

закріпити навички розв'язування задач за виведеною 
формулою;   

• розвиваючі: розвиток уяви, мислення, порівняння, узагальнення;   

• виховні: формування комунікативних умінь   

Тип уроку: урок вивчення нового матеріалу та первинного закріплення   
нових знань.  

Технологія навчання: особистісно-орієнтована   

Форма організації навчальної діяльності: індивідуальна, фронтальна,   
робота в групах   

Методи навчання: репродуктивний, частково-пошуковий.  

Обладнання: комп'ютер, мультимедійна дошка, роздатковий матеріал -  
трикутники, чотирикутники, трапеції

.   
Хід уроку

І. Організаційний момент

Сьогодні у нас пошуково - дослідна робота. Ми з вами згадаємо   

все, що вивчили про площі. Спробуємо зробити відкриття нової   

формули. Адже ми сьогодні з вами - дослідники!

II. Перевірка домашнього завдання  

1. Що ми з вами вивчали на попередніх уроках? (Вивчали формули   

площі квадрата, прямокутника, паралелограма, ромба,   

трикутника.)   

2. Що розуміють під площею многокутника? (Площа - це величина   

тієї частини площини, яку займає даний многокутник.)   

3. Чим виражається площа? (Площа виражається додатним   

числом. Це число показує, скільки разів одиниця виміру вкладається у 
многокутнику.)   

4. Що прийнято за одиницю площі? (За одиницю вимірювання площі   

приймають площу квадрата зі стороною, що дорівнює одиниці довжини).   

5. Які одиниці вимірювання площ ви знаєте? (1мм2 , 1см2 , 1дм2 , 1м2 ,1км2;

1 а, 1 га - у сільському господарстві; 1 барн = 10-28 м2  - у хімії та фізиці).

6. Назвіть властивості площ.   

- Властивість 1. Рівні многокутники мають рівні площі

- Властивість 2. Якщо многокутник складаєтся з кількох многокутників, то 

його площа дорівнює сумі площ цих многокутників.

 - Властивість 3. Площа квадрата дорівнює квадрату його сторони.

7. Як можна знайти площу довільної геометричної фігури? (За   

допомоги палетки, але це не зовсім зручний спосіб, та й не точний)   

- Палетка (від франц. palette - пластинка, планка), накреслена на прозорому 
папері, склі або целулоїдній платівці сітка ліній, що утворюють   

квадрати відомих розмірів, за допомогою яких визначається площа   

ділянок на плані або карті.

8. Площі яких геометричних фігур ми вміємо знаходити? Як?

(Площа квадрата, прямокутника, трикутника, паралелограма, ромба.)

9. Для  чого потрібно знати та вміти знаходити площі фігур? Де це   

застосовується на практиці? (У будівництві, у сільському господарстві.)   

- Коли почали застосовувати площі та з якою метою?   

Історична довідка  

- Геометрія, як і інші науки, виникла з потреб практики. Саме   

слово "геометрія" - грецьке, у перекладі означає "землемірство". Люди   

дуже рано зіткнулися з необхідністю вимірювати земельні ділянки. Уже за 3-4  тис.років до н.е. кожен клаптик родючої землі в долинах Нілу,   

Тигру і Євфрату, річок Китаю мав значення для життя людей. Після розливу 
річок, особливо Нілу, доводилося знову ділити землю. Це вимагало   

певних знань. За єгипетськими папірусами, що дійшли до нас, і   
давньовавилонськими текстами видно, що вже за 2 тис. років до н.е. люди 
вміли    визначати площі трикутника, квадрата, прямокутника, трапеції.   

Розвиток архітектури висунув геометрії нові вимоги. І в Єгипті, і у Вавилоні 
споруджували колосальні храми, будівництво яких могло здійснюватися 
тільки на основі попередніх розрахунків площ.   

Тому дуже важливо знати, як обчислюються площі фігур і вміти їх   
обчислювати.   

1) Тест для перевірки теоретичного матеріалу   

1. Виберіть правильні твердження:   

а) площа прямокутника дорівнює добутку двох його сторін;   

б) площа квадрата дорівнює квадрату його сторони;   

в) площа прямокутника дорівнює подвоєному добутку двох його   

сусідніх сторін.   

2. Закінчіть фразу: площа ромба дорівнює половині добутку...   

а) його сторін;   

б) його сторони та висоти, проведеної до цієї сторони;   

в) його діагоналей.   

3. За формулою S= a∙hа можна обчислити площу:   

а) паралелограма;   

б) трикутника;   

в) прямокутника. 

4. Виберіть правильне твердження. Площа прямокутного   

трикутника дорівнює:   

а) половині добутку його сторони на будь-яку висоту;   

б) половині добутку його катетів;   

в) добутку його сторони на проведену до неї висоту.   

5. Площу трикутника за відомими трьома сторонами можна   

обчислити за допомогою:   

а) теореми Піфагора;   

б) теореми Фалеса;   

в) формули Герона.   

(Взаємоперевірка.Кожне завдання оцінююєтся у 2 бали)

Відповіді: 1) а, б; 2) в; 3) а; 4) б; 5) в.    

III. Актуалізація опорних знань

Обгрунтуйне відповідь 

- Фігура є опуклим многокутником .   

- Сума її внутрішніх кутів 360 градусів.   

- А сума внутрішніх кутів, прилеглих до однієї сторони ,180 градусів.   

- Цю фігуру можна розбити  на паралелограм і трикутник.   

- Що це за фігура?   

- Правильно, це трапеція! Отже, сьогодні ми поговоримо про трапецію та   

 виведемо формулу знаходження площі трапеції.    

IV. Сприйняття та осмислення нового матеріалу

Тема уроку: "Площа трапеції".   

- Яке запитання ви зараз собі ставите? (як знайти площу трапеції, для   

чого це потрібно знати і де це буде використовуватися?)   

- Отже, ви зараз самостійно  сформували мету нашого уроку: знайти зручний 
спосіб обчислення площі трапеції. Пошуками цього способу ми зараз і 
займемося.   

- Спочатку пригадаємо визначення трапеції. (Трапеція - це   

чотирикутник, у якого дві сторони паралельні, а дві інші - ні.)  - Як 
називаються сторони трапеції? (Основи та бічні.) 

- Яке інше значення має це слово? (Трапеція - цирковий снаряд;  трапеція - стиль одягу.)   

- Слово "трапеція" - походить від слова "трапеза" - це обід у ченців ,або столик  для їжі.   

- Як ви думаєте, чому? (Трапеція схожа на столик.)   

- Сьогодні ми будемо шукати зручніший, точніший спосіб знаходження площі  трапеції. У кожного з вас на столі лежать моделі трапеції. Ви   

можете розрізати її на такі фігури, площі яких ми вміємо знаходити.  Можете  розбивати за допомогою олівця та лінійки,Використовуючи властивості   

площ, знайдіть площу трапеції.   

- Як потрібно поводитися з ножицями? (Обережно, передавати тільки   

тупими краями.)   

- Отже, працюємо! (Учні працюють: розрізають трапеції на частини,   
виконують необхідні вимірювання та обчислюють площі отриманих   

фігур.)   

- Підіб'ємо підсумки: назвіть ваші результати: Sтр. = ...   

- Як ви знаходили Sтр. ?   

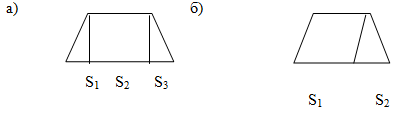
- Який спосіб найкращий? (Останній.)

   == , де а і в - основи, h - висота.   

Ура! Ми з вами зробили відкриття!   

- У групах обмінятися інформацією про способи знаходження площі   

трапеції.   

Можливі варіанти запропонованих рішень (всього 12 способів) - і це не межа.   

1. S трапеції=S трикутника +S прямокутника +S трикутника.   

2. S трапеції = S великого трикутника - S маленького трикутника.   
3. S трапеції=S паралелограма - S трикутника.   

4. S трапеції=S прямокутника - S трикутника -S трикутника.   

5. S трапеції=S трикутника +S трикутника.   

6. S трапеції=S паралелограма +S трикутника.   

- У групах обговорити варіанти словесних формулювань формули для   
знаходження площі трапеції.   

Кожна група пропонує свій варіант формулювання. Після спільного   

обговорення обирається найкращий варіант.   

- Порівняти отриману формулу та формулювання із запропонованими в   
підручнику. Кожен учень записує в зошит формулу площі трапеції   

і формулювання, обране ним.   

V. Первинне закріплення вивченого матеріалу  

Задача

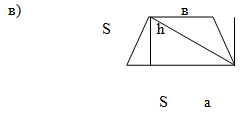
      У трапеції ABCD з основами AB і CD  проведено висоту CH. Знайдіть площу трапеції, якщо:
Знайдіть площу трапеції, якщо:
АВ=60 см,   CD=36 см,  СН=50 см.

1.     Дано: ABCD- трапеція, АВ=60 см,   CD=36 см,  СН=50 см.

Знайти:

Розв’язання:

За теоремою про площу трапеції

= 2400 (

Відповідь: 2400

      Фізкультхвилинка

VI. Осмислення об*єктивних зв*язків

Задача

Площа трапеції дорівнює S,  а її висота – h. Знайдіть суму основ трапеції.
S=60 , h=12 см.
Дано: S=60 , h=12 см.

Знайти: (a+b)

Розв’язання:

За теоремою про площу трапеції

  → = = 10(cм)

Відповідь: 10 см.

Дослідження задачі при зміні фігури.   

Можна запропонувати відповісти на запитання   

дослідницького характеру:   

1. Чи завжди трапецію можна розбити на три рівні трикутники?   

Це можна зробити тільки тоді, якщо одна основа вдвічі більша за   

іншої.   

2. Чи може трапеція бути складена з трьох рівних трикутників іншого виду?   
Трапецію можна скласти з трьох правильних трикутників, рівнобедрених і довільних трикутників.   

3. Чи зберігатимуться способи розв'язання в цих випадках? Які способи будуть    найбільш раціональними?   

VII. Підсумок уроку. Рефлексія.  

- Хто працював сумлінно?   

- Хто брав участь у будівництві храму знань?   

VIII. Домашнє завдання: