Урок "Формули коренів квадратного рівняння"

Про матеріал

Матеріал містить розробки трьох уроків з теми: "Формули коренів квадратного рівняння"

Перегляд файлу

План конспект уроку алгебри в 8 класі з теми:

«Формули коренів квадратного рівняння»

Мета:

Навчальна

познайомити учнів з основними формулами знаходження коренів повного квадратного рівняння;
познайомити з правилами оформлення розв’язку квадратного рівняння;
формувати вміння знаходити корені квадратного рівняння, використовуючи його означення та формули;
домогтися засвоєння формул коренів квадратного рівняння.

Розвиваюча

розвивати обчислювальні навички, уміння аналізувати й узагальнювати;
розвивати інтерес до математики.

Виховна

виховувати позитивне ставлення до навчання, почуття відповідальності,

активність, культуру емоцій, точність, акуратність.

Задачі уроку: познайомити учнів з поняттям дискримінанту, вивести формулу коренів квадратного рівняння, учити застосовувати її при розв ’язуванні квадратних рівнянь.

Тип уроку: засвоєння нових знань та вмінь.

Обладнання уроку: комп’ютери, проектор, роздавальний матеріал, зошит, підручник, довідники.

Якщо ти почуєш, що хтось не полюбляє математику - не вір.

Її не можна не любити - її можна тільки не знати.

Хід уроку

Органійзаційний етап.

Добрий день, шановні діти та гості, які присутні на нашому уроці.

Сценка. (До класу заходить учень, який сильно хромає).

Що трапилось?
Я бігав по коридору та впав. Здається, що вивихнув ногу.
Чим же ми можемо тобі допомогти?
Ви ж займаєтеся алгеброю? Значить, ви і зможете мені допомогти.
Дивно! Хоча ... (слайд Сценка)

Повідомлення учня. Термін "алгебра", як назву мистецтва відновлення, у арабів перейшов і в медицину. Мистецтво лікаря "костоправа" так само називали алгеброю, а самого лікаря - алгебраїстом.

Вчитель: Це все вірно, але ми тобі допомогти нічим не зможемо. Ми вивчаємо алгебру, квадратні рівняння. Алгебра від слова "аль - джебр" - відновлення, заповнення або "перенесення доданків з однієї частини рівняння в іншу". Вибач, тобі необхідно звернутись до лікаря.

Перевірка домашнього завдання, актуалізація опорних знань.

Перевірка домашнього завдання за заздалегідь записаними відповідями на дошці.
Фронтальне опитування (слайд Актуалізація )

? Які рівняння ви бачите на екрані? /Квадратні7

? Доведіть, що дані рівняння квадратні.

? Перелічіть види квадратних рівнянь, які зображені на екрані. /Неповні квадратні рівняння, повні квадратні рівняння, зведені квадратні рівняння).

? Які методи ви застосовуєте при розв’язанні квадратних рівнянь?

/1. При роз’вязку неповних квадратних рівнянь треба застосувати означення

квадратного кореня (коли немає доданку при х), або винесенням х за дужки; 2.

а) а=1, b=-2, с=3;

б) b=4, а=-1, с=4;

в) с=-5; а=2, b=-1;

г) b= 0, с=9; а=-1

а) а=2, b=-1, с= 5;

б) b=-5, с= 3; а= - 1;

в) с= -4; b= 2; а= -3;

г) с=0, а=5; b= - 3

3)Виділіть квадрат двочлена:

а) 4х² + 20х +31;

б) х² + 10х + 16

а) 9х² + 24х + 20;

б) х² + 14х + 25

Вивчення нового матеріалу

Мотивація (слайд Мотивація, звернення учнів 5 класу за поміччю у розв 'язку задачі)

- Шановні учні 8 класу. При підготовці до олімпіади з математики, ми розв’язували задачу на складання рівняння, але наших знань не вистачає, щоб отримати відповідь, допоможіть нам.

Життєва задача: Фермер виділив під баклажани ділянку прямокутної форми розмірами 8 * 10 м. Для захисту від шкідливих комах він висадив базилік уздовж двох сусідніх сторін ділянки, як показано на малюнку. Визначте ширину смуги, зайнятої базиліком, якщо загальна площа, зайнята базиліком і баклажанами, становить87,36 м² .

Розв’язання

Якщо позначити ширину смуги, яку виділено під базилік,через х м, то сторони прямокутника, що містить і баклажани, і базилік, дорівнюватимуть (8+х) м і (10+ х) м. Оскільки загальна площа ділянки становить 87,36м² , то складемо рівняння:

(8+х) *(10+х ) = 87,36.

(Один учень виходить до дошки й починає розв’язувати рівняння інші записують у зошити)

(8+х)-(10+х) =87,36;

80+8х+10х+х²=87,36; х²+18х+17,36=0

- Отже, розв’язання задачі зводиться до розв’язання рівняння, що відрізняється від неповних квадратних рівнянь та й спосіб виділення квадрата двочлена у повному квадратному рівнянні тут не ефективний. Треба застосувати інший спосіб розв’язку повного квадратного рівняння.

? Яку мету ми перед собою поставимо на цьому уроці? (Спробувати знайти інший спосіб розв ’язку квадратних рівнянь)

- Запишемо тему урока «Формули коренів квадратного рівняння»

Відкриття нових знань.

Історія алгебри поглиблюється своїми коренями в давні часи. Задачі,які пов’язані з рівняннями розв’язувались ще у Древньому Єгипті та Вавілоні. Теорія рівнянь цікавила та цікавить математиків усіх часів та народів. У Древній Індії були поширені публичні змагання по розв’язку важких задач. Ввиведення формули коренів квадратного рівняння в загальному вигляді є у Вієта, але він признавав тільки додатні корені. Італійські математики 16 ст. визнають додатні та від’ємні числа. Тільки в 17 ст. завдяки працям Ньютона, Декарта та інших вчених спосіб розв’язку квадратних рівнянь приймає сучасний вигляд. Над проблемою розв’язку квадратних рівнянь математики бились на протязі декількох століть.

Сьогодні ви легко навчитись розв’язувати любе квадратне рівняння, на заздрість математикам Древньої Греції та Індії.

- Щоб кожного разу не проводити великі обчислення, нам досить одного разу розв’язати рівняння в загальному вигляді та отримати готові формули для коренів квадратного рівняння.

(Вчитель виводить формули на дошці, учні записують у довідники з

математики) ах²+ bх+с = 0

Спробуємо встановити, як зв’язані корені квадратного рівняння з числами а, Ь, с. Числа а, Ь, с ми бачимо в квадратному рівнянні, а коренів - ні. Будемо шукати корені.
Спочатку виділимо в рівнянні повний квадрат. Для цього розділимо рівняння на старший коефіцієнт а.

х² +b/a х + c/a = 0

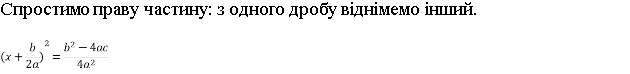
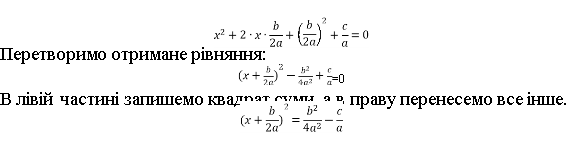
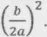
$C:\Users\Admin\AppData\Local\Temp\FineReader12.00\media\image2.jpeg$

Отримали формулу квадрата суммы: спочатку додамо, а потім віднімемо вираз

Дискримінант розрізняє квадратні рівняння по кількості коренів. В залежності від значення дискримінанту квадратне рівняння може мати один чи два кореня, а може не мати коренів зовсім. Роздивимось кожний з цих випадків.

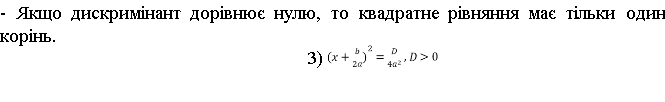
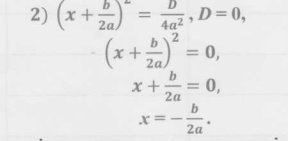
$C:\Users\Admin\AppData\Local\Temp\FineReader12.00\media\image3.jpeg$

Якщо дискримінант більше за нуль, то квадратне рівняння має рівно - -- - Якщо дискримінант більше за нуль, то квадратне рівняння має рівно два різних дійсних кореня. Отримати їх можна за готовою формулою. А отримані при цьому формули ми й будемо використовувати в подальшому для знаходження коренів.

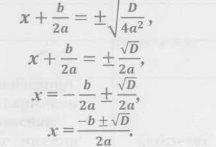
$C:\Users\Admin\AppData\Local\Temp\FineReader12.00\media\image4.jpeg$

формула коренів квадратного рівняння (слайд Опорний конспект)

Засвоєння нових знань і вмінь 1) Первинне закріплення

Складемо блок-схему розв’язку квадратних рівнянь

? При розв’язанні повното квадратного рівняння, що в першу чергу обчислюється/Дискримінант/

? Якщо треба скласти програму для обчислення квадратного рівняння, то яку команду використовували? /Команду розгалуження/

- Давайте складемо блок-схему для обчислення квадратного рівняння.

? Які дані вхідні?

? Які дані вихідні?

? Які дані не ввійшли до вхідних та вихідних даних? Чому?

/На дошці будується блок-схема програми/

? В яких програмах можна скласти програму обчислення коренів квадратного рівняння? /Паскаль, Ексель/

2) Робота за підручником

№ 1 Розв’язати рівняння:

Зх² + 8х - 11 = 0.

а = З, b= 8, с = —11

D=b²-4ac=8²-4*3*(-11)=64+132=196,D>0

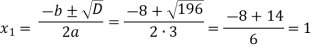
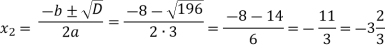
Відповідь. 1;-3:

№ 2. Розв’язати рівняння:

- 9х²+6х- 1=0.

Як показує досвід зручніше мати справу з квадратними рівняннями, у яких старший коефіцієнт додатній. Тому спочатку помножимо обидві частини рівняння на (-1), отримаємо:

9Х²- 6х + 1 = 0

D=0,

9х² — х + 3,5 = 0.

D = -27, D<0. Рівняння коренів не має.

4)Робота з класом

№ 4 х² - 5х + 6 = 0, D = 1, х₁ = 2, x₂= 3;

№ 5 х² — 2х — 15 = 0, D = 64, х₁= —3, x₂ = 5.

5)Виконання завдань на картках із друкованою основою

- Два учні за комп’ютером в програмах Паскаль та Ексель запрограмують розв’язок повного квадратного рівняння, всі інші розв’язують в зошитах рівняння, а в таблицю вносять дані, потім перевіряють виконання на комп’ютері.

Завдання: Заповнити таблицю, де а, b, с — коефіцієнти квадратного рівняння виду ах²+ bх +с = 0, D - його дискримінант, х₁ і x₂ - корені.

Варіант 1

Рівняння	а	b	с	D	Х₁	X₂
х² + 42х + 441 = 0		-
х² + 8х + 7 = 0
Зх²-13х+ 14 = 0

Варіант2

РІВНЯННЯ	а	b	с	D	Х₁	X₂
х² - 34х + 289 = 0
х² + 4х - 5 = 0
2х²-9х+ 10 = 0

Підбиття ПІДСУМКІВ уроку

Яку мету ми поставили перед собою на цім уроці?
Чому вона виникла?
Чи досягли ми своєї мети?

- Діти, прочитайте прислів'я "Математика - гімнастика розуму".

? Що таке гімнастика?

Вислухавши відповіді, вчитель підводить підсумок:

Гімнастика - це система вправ для фізичного розвитку людини; гімнаст - людина спритна, стрункий, сильний, пластичний, гарний.

Математика також багато дає для розумового розвитку людини - змушує думати, міркувати, шукати прості і красиві рішення, допомагає розвивати логічне мислення, вміння правильно і послідовно міркувати, тренує пам'ять, увагу, загартовує характер.

Домашнє завдання

Самою важкою й важливою справою для кожного учня є виконання домашнього завдання. Якщо домашнє завдання виконано правильно, то на уроці ви відчуваєте себе набагато впевненіше.

§21 - читати, вивчити означення, алгоритм розв’язку рівнянь, № 813, № 815

Додаткове завдання: При яких додатних значеннях т обидва корені рівняння 0,25х²+7х+m=0 рівні між собою?

Хто хоче обмежитися теперішнім, має знати: без знання минулого, не зрозуміє його.

Лейбніц

Тема: Формула коренів квадратного рівняння.

Мета:

Освітня: домогтися засвоєння учнями змісту поняття «дискримінант квадратного рівняння», формули дискримінанта та схеми виводу формул розв'язування квадратного рівняння загального вигляду, а також формул коренів квадратного рівняння; сформувати первинні вміння знаходити за

формулами дискримінант квадратного рівняння, за його значенням визначати

кількість розв’язків квадратного рівняння й обчислювати корені квадратного рівняння;

Розвиваюча: розвивати розумову діяльність;

Виховна: виховувати самостійність, намагатися скласти ситуацію успіху для кожного учня.

Мета для учнів;

засвоїти поняття «дискримінант квадратного рівняння», формули дискримінанта та схеми виводу формул для розв’язування квадратного рівняння загального вигляду, а також формул коренів квадратного рівняння; навчитися знаходити за формулами дискримінант квадратного рівняння, за його значенням визначати кількість розв’язків квадратного рівняння й обчислювати корені квадратного рівняння.

Тип уроку: засвоєння нових знань та вмінь.

Наочність та обладнання: комп’ютер, презентація, роздавальний матеріал.

Хід уроку

Організаційний етап
Перевірка домашнього завдання

Самостійна робота( робота в парах)

Варіант 1

Варіант 2

1. Розв’яжіть рівняння:

а) 5х² -20 = 0; б) х² + 7х = 0;

в) х² +25 = 0

а) Зх² —27 = 0;б) х²-х = 0;

в) х² +36 = 0

Актуалізація опорних знань( фронтальне опитування)

Які рівняння називаються квадратним? Наведіть приклади.
Як називаються коефіцієнти квадратного рівняння

ах² + bх +с =0?

Які квадратні рівняння називаються неповними? Наведіть приклади.
Скільки коренів мають неповні квадратні рівняння кожного виду?
У квадратному рівнянні назвіть старший коефіцієнт, другий коефіцієнт і вільний член:

а) 2х² + Зх -4 =0;

б) 13х -5х² +1=0;

Мотивація навчальної діяльності

1. Розв’яжіть рівняння:

а) х² = 25; б) (х +2)² = 0. в ) х²-6х + 9 = 0; г) 2х² + Зх-4 =0?

Застосування основних властивостей значно полегшує розв’язання багатьох рівнянь.

Отже, сьогодні на уроці ми з вами, знайдемо єдиний достатньо простий алгоритм розв’язання квадратних рівнянь загального вигляду. Розв’язання цієї проблеми і є головною метою уроку

Оголошення теми і мети уроку.

V. Вивчення нового матеріалу План вивчення теми

Виведення формули коренів квадратного рівняння.
Алгоритм розв’язання квадратного рівняння за формулою.
Кількість дійсних коренів квадратного рівняння.
історична довідка.

Вивчення нового матеріалу проводиться за допомогою комп’ютера.

Пояснення вчителя супроводжується презентацією створеною на комп’ютері.

ах² + bх + с =41

Вираз b² - 4ас називають дискримінантом даного квадратного рівняння. Позначають D

Якщо D < 0, то дане рівняння не має коренів.

Якщо D = 0, то х= 0 - єдиний корінь х=-b/2a .
Якщо D > 0, то дане квадратне рівняння має два корені, які відрізняються тільки знаками перед 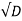. Коротко записують їх так:

- це формула коренів квадратеного рівняння ax²+bx+c=0.

Користуючись нею можна розв’язати будь-яке квадратне рівняння. Дану формулу застосовують для розв’язування багатьох рівнянь, які зводяться до квадратних.

Розглянемо приклад. Розв’яжіть рівняння

Зх² + 5х +2 =0:

D= 25 -24=1, D>0, - рівняння має два корені.

Історична довідка

Першим, хто описав розв’язок квадратних рівнянь, був Мухамед-аль-Хорезми, який написав трактат „Аль-Джебра і Аль-Мухабала”. В перекладі на теперішній язик, аль-джабр означає перенесення доданків з однієї частини в другу, а аль- мухабала - зведення подібних доданків.

Способи розв’язування квадратних рівнянь знаходили у вавилонян, Евклида і Диофанта.

Фізична хвилинка

VI. Формування вмінь

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв’язати завдання та кого змісту:

Знаходження дискримінанта квадратного рівняння та визначення кількості коренів цього рівняння.

1) Для квадратного рівняння знайдіть дискримінант і вкажіть кількість його коренів:

а) 2х² - Зх +1 = 0; б) 4х² + 4х +1 = 0; в) -Зх² + 6х - 4 = 0.

Розв’язування квадратного рівняння за формулою.

1) Розв’яжіть рівняння:

а) х² - 6x + 5 = 0; б) х² + 4х -12 = 0; в) х² + 7х +10 = 0;

Не розв’язуючи квадратного рівняння, вказати ті з них, які мають задану кількість коренів.

Не розв’язуючи рівняння, вкажіть ті з них, які мають один корінь: а) 9х²+6х + 1 =0; 6) Зх²-х-4 = 0; в) 2х²-16х + 32 =0.
Яке з рівнянь не має коренів:

а) х² + 2х—7 = 0; б) 2х²-Зх+8 = 0; в) Зх²+5х+4 = 0?

VII. Підсумки уроку

Прес — конференція.

Обговорення того, наскільки повно було виконано роботу, в якому напрямку необхідно працювати далі.

В якому випадку правильно знайдено дискримінант?

а) 5х² +Зх + 2 = 0, D> = 49;

б) 2х² -Зх-5 = 0,D> = 49;

в) 2х²-Зх + 5 = 0,D= 49.

виставлення оцінок

VIII. Домашнє завдання

♦

Вивчити формули коренів квадратного рівняння.
Розв'язати приклади на застосування цих формул. За підручником Початковий, середній рівень

Достатній Високий

І) Доведіть, що при будь-якому значенні змінної значення виразу додатне:

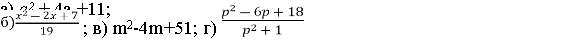
На повторення:

Рефлексія

Урок № 49
(алгебра 8 клас)

Тема. Формула коренів квадратного рівняння

Мета: домогтися засвоєння учнями змісту поняття «дискримінант квадратного рівняння», формули дискримінанта та схеми виводу⁷ формул для розв'язування квадратного рівняння загального вигляду, а також формул коренів квадратного рівняння; сформувати первинні вміння знаходити за формулами дискримінант квадратного рівняння, за його значенням визначати кількість розв'язків квадратного рівняння й обчислювати корені квадратного рівняння.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Квадратні рівняння».

Хід уроку

І. Організаційний етап

II. Перевірка домашнього завдання Самостійна робота 10

Варіант 1	Варіант 2
1. Розв'яжіть рівняння:
а) Зх² - 20 = 0; б) х² + 7х = 0;	а) Зх²-27 = 0; б)х²-х = 0;
в) х² + 25 = 0	в) х² + 36 = 0
2. Знайдіть корені рівняння:
а) (2х — 7)²— 7(7 — 4х) = 0;	а) (х - 5)² + 5(2х — 1) = 0;
б) (Зх — І)²—(Зх — 1) = 0	б) (2х-3)²-2(2х —3) = 0
3. При якому значенні а корені рівняння
х² + (а — 2)х + а —6 = 0	х²+(п+ 1)х + а - 8 = 0
будуть протилежними числами?

III. Формулювання мсти і завдань уроку

З метою створення відповідної мотивації пропонуємо учням розв'язати низку рівнянь: кілька з них — неповні квадратні рівняння, а інші — квадратні рівняння загального вигляду, причому два з них такі, що повний квадрат виділяється легко (наприклад, зведені квадратні рівняння з парними другими коефіцієнтами), а два такі, що виділення повного квадрата ускладнене (квадратні рівняння, що не є зведеними). Аналіз ситуації, що склалась, приводить до формулювання проблеми: необхідно знайти єдиний достатньо простий алгоритм розв'язання квадратних рівнянь загального вигляду. Розв’язання цієї проблеми І є головною метою уроку.

IV. Актуалізація опорних знань та вмінь

3 метою успішного сприйняття учнями навчального матеріалу перед його вивченням слід активізувати такі знання і вміння учнів: прийоми виділення квадрата двочлена з даного квадратного тричлена; обчислення значень змінних за формулами розв’язання рівнянь виду х²=а.

Виконання усних вправ

а)х² = 25; б) 4х² = 1; в) 3х² = 6; г) (х- 1)² = 25; д) (х + 2)³ = 0.

Замініть рівняння рівносильними зведеними квадратними рівнянням: а) 2х² - 6х + 10 = 0; б) Зх² — 12х² + 3 = 0; в) 2х + 0,5х² -1=0;

г) -х² + х— 7 = 0.

Подайте тричлен, якщо можливо, у вигляді квадрата двочлена:

а) х² + 2х + 1; б) 2а +а² — 1; в) х² + 1 - 2х; г) х² + 6х + 9;

д) у²-8у + 64; е) 36+ 12а + а²); ж) х²-2/3х+1/9.

Засвоєння знань

План вивчення нового матеріалу

Виведення формули коренів квадратного рівняння. Схема розв'язання квадратного рівняння загального вигляду за формулою.
Приклади застосування виведеної формули.

Виведення формули коренів квадратного рівняння загального виду традиційно здійснюється у формі розв'язування квадратного рівняння загального вигляду виділенням квадрата двочлена. І хоча перед цим уроком було розв'язано вправи на повторення (на поновлення навичок „ виділення квадрата двочлена), виведення формули може викликати певні труднощі, бо пов'язане з перетвореннями виразів з буквеними коефіцієнтами. Тому, щоб подолати такі труднощі, перед виведенням формули можна ще раз показати всі перетворення на прикладі рівняння з числовими коефіцієнтами, а потім переходити до роботи з буквеними виразами (або ж у випадку невисокого рівня математичних здібностей учнів подати їх у вигляді готових формул).

Після виведення формули важливо дати учням схему дій із застосування виведених формул у вигляді алгоритму.

Розглядаючи приклади на застосування виведених формул, бажано звернутися до всіх можливих випадків (дискримінант додатний, від'ємний та дорівнює нулю). Під час розв'язування квадратного рівняння, дискримінант якого дорівнює нулю, слід показати два способи знаходження коренів (двох рівних): за виведеною формулою (яку в 9 класі будемо вивчати як формулу абсциси вершини параболи — графіка квадратичної функції у = ах² + bх + с), а також розкладанням лівої частини рівняння на множники за формулою квадрата двочлена (цей спосіб стане у пригоді для побудови графіка квадратичної функції шляхом геометричних перетворень графіка функції

Y=x²

Формування вмінь

Виконання усних вправ

1. Знайдіть значення виразу b² - 4ас:

а) а = 1; b = 2; с = 3; б) а = 2; b = 5; с = -3.

2. Знайдіть значення виразу :

а) b =-1; D = 9; а = 2; б) b = -3; D= 25; а = -2.

3. Скільки коренів має рівняння ax² + bх + с = 0, якщо значення виразу

b² - 4ас для нього дорівнює: а) 25; б) 3; в) -1; г) 0?

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв’язати завдання такого змісту:

Знаходження дискримінанта квадратного рівняння та визначення кількості коренів цього рівняння.

Для квадратного рівняння знайдіть дискримінант і вкажіть кількість його коренів:

а) Зх²— Зх +1=0; б) 4x² + 4х + 1 = 0; в) -Зх² + 6х - 4 = 0.

Обчисліть дискримінант квадратного рівняння і вкажіть число його коренів:

а) 2х² + Зх + 1 = 0; б) 2х² + х + 2 = 0; в) 9x² + 6х + 1 = 0; г) х² + 5х - 6 = 0.

Розв’язування квадратного рівняння за формулою.

Розв'яжіть рівняння:

а) х² — 6х + 5 = 0; б) х² + 4х - 12 = 0; в) х² + 7х + 10 = 0; г) х² - Зх + 4 = 0;

д) х² — 10х + 25 = 0; є) х² - 4х - 21 =0.

Розв'яжіть рівняння:

а) 2х² - 5х + 3 = 0; б) Зх² + х — 1 = 0; в) Зх² + 5х - 2 = 0; г) 4x² - 4х + 1 = 0;

д) 2x² - Зх + 2 = 0; є) 7х² — 6х — 1 =0.

Розв'яжіть рівняння:

а) Зх² - 7х + 4 = 0; б) 5x² - 8х + 3 = 0; в) Зх² - 13х + 14 = 0;

г) 2у²-9у + 10 = 0; д) 5у²— 6у + 1 = 0; є) 4x² + х - 33 = 0;

ж)y²- 10у-24 = 0;з)р² +р-90 = 0. ,

Не розв’язуючи квадратного рівняння, вказати ті з них, які мають задану кількість коренів.

Не розв’язуючи рівняння, вкажіть ті з них, які мають один корінь: а) 9x² + 6х + 1 =0; б) Зх²-х — 4 = 0; в) 2x²— 16х + 32 = 0.
Яке з рівнянь не має коренів:

а) х² + 2х — 7 = 0; б) 2x²— Зх + 8 = 0; в) Зх² + 5х + 4 = 0?

Розв'язування квадратного рівняння найбільш зручним способом (завдання передбачає повторення поняття неповного квадратного рівняння та способів його розв'язання в поєднанні з вивченим на уроці способом розв'язання квадратних рівнянь загального виду).
Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

Знайдіть значення Ь. при яких один із коренів рівняння дорівнює -3:

а)20х² + bх – b² = 0; б) .

2) Доведіть, що при будь-якому значенні змінної значення виразу додатне:

а)а²+4а+11;б) ; в) m²-4m+51; г)

$C:\Users\Admin\AppData\Local\Temp\FineReader12.00\media\image10.jpeg$

Письмові вправи мають на меті засвоєння формул коренів квадратного рівняння (формули дискримінанта, самих коренів) та формування вміння застосовувати ці формули (нові знання) в поєднані з вивченими раніше способами розв'язання квадратних рівнянь (вивчений раніше матеріал). Оскільки на цьому уроці лише починається робота із закріплення знань формул коренів квадратного рівняння, з метою попередження помилок та кращого запам'ятовування вивчених формул, слід вимагати від учнів строгого дотримання алгоритму та усного й письмового відтворювання виведених формул (доцільно використати такий мнемонічний прийом: запам'ятовування формул у вигляді речення — «де дорівнює бе квадрат мінус чотири а це», або використовувати інші мнемонічні прийоми).

Якщо засвоєння нового матеріалу проходить успішно, то вже на цьому уроці можна запропонувати учням завдання, що передбачає поєднання нових знань і вмінь (формул коренів квадратного рівняння та первинних умінь їх застосовувати) із набутими раніше знаннями та вміннями (види квадратних рівнянь та вміння визначати вид квадратного рівняння — зведене або неповне певного виду, та способів розв'язання неповних квадратних рівнянь).

Підсумки уроку

В якому випадку правильно знайдено дискримінант?

а) 5x² + Зх + 2 =0, D = 49; б) 2x²— 3x- 5 = 0, D = 49;

в) (Зх – 2)(Зх + 2) = бх+3, D = 49; г) 2х²-Зх + 5 - 0, D = 49.

Домашнє завдання

Вивчити формули коренів квадратного рівняння.
Розв'язати приклади на застосування цих формул.
На повторення: підібрати приклади завдань на перетворення виразів, що містять квадратні корені, розв'язування яких передбачає винесення множника з-під знака кореня, та завдання на скорочення дробів.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Пархоменко Любов Романівна

Пов’язані теми

Алгебра, Розробки уроків

Додано

25 лютого 2021

Переглядів

2526

Оцінка розробки

Відгуки відсутні