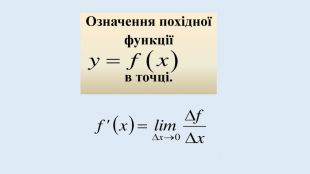Презентація. "Похідна. Геометричний та маханічний зміст похідної"
Про матеріал
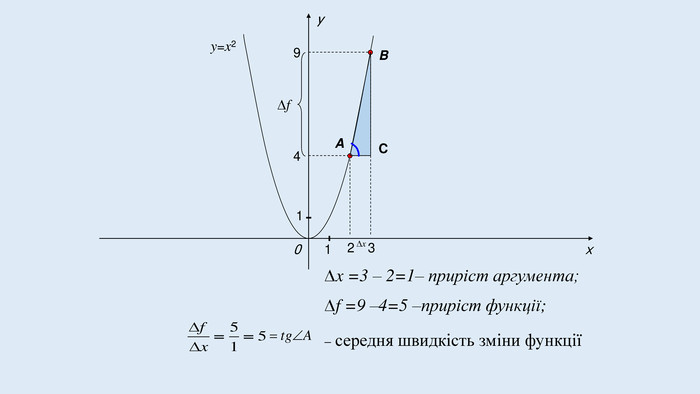
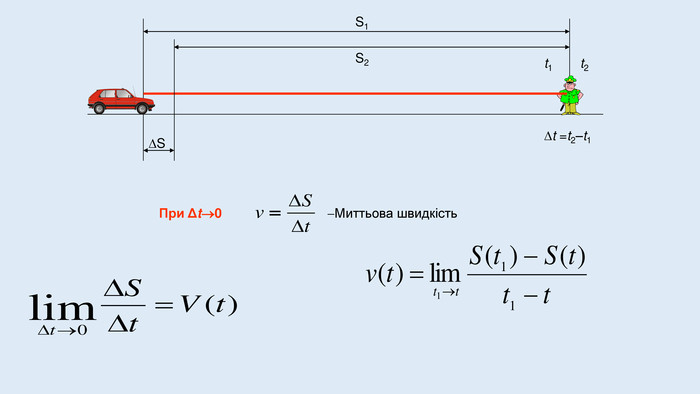
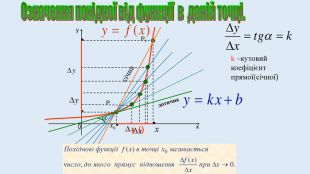
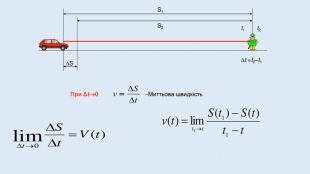
Поняття похідної - фундаментальне поняття математичного аналізу, за допомогою якого досліджують процеси і явища в природничих, соціальних і економічних науках. Вивчення різних процесів(механічного руху, хімічних реакцій, розширення рідини при нагріванні та ін.) приводять до необхідності обчислення швидкості зміни різних величин, тобто до поняття похідної.
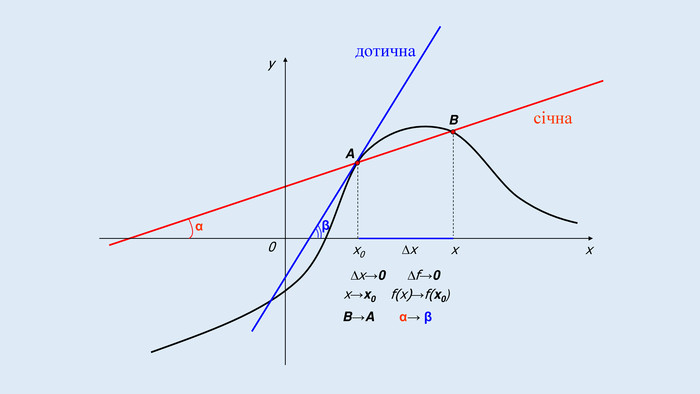
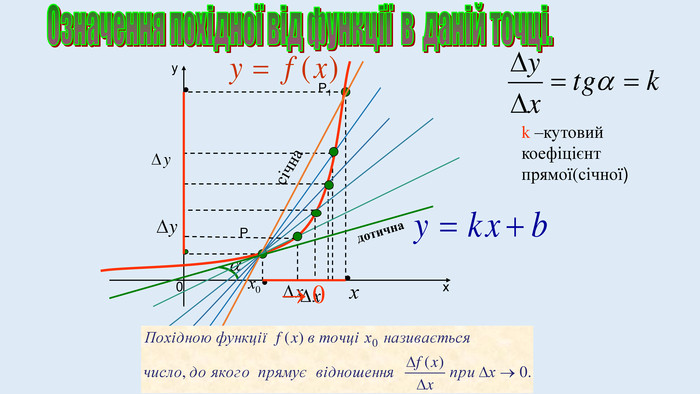
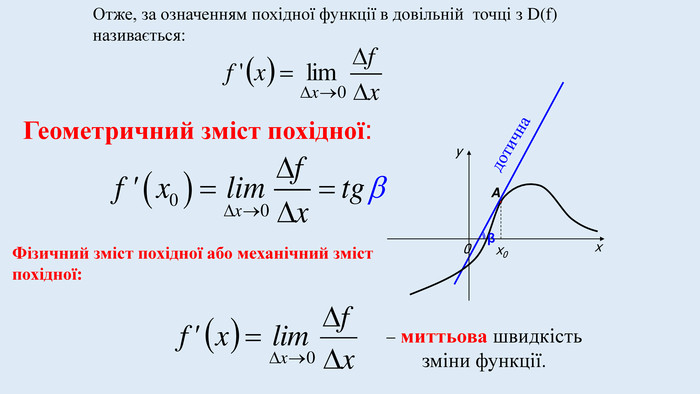
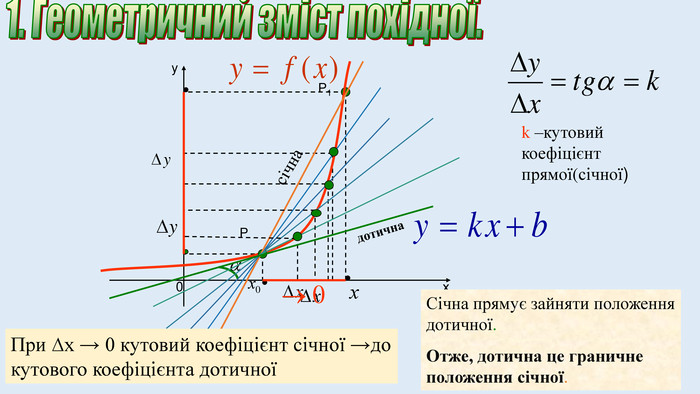
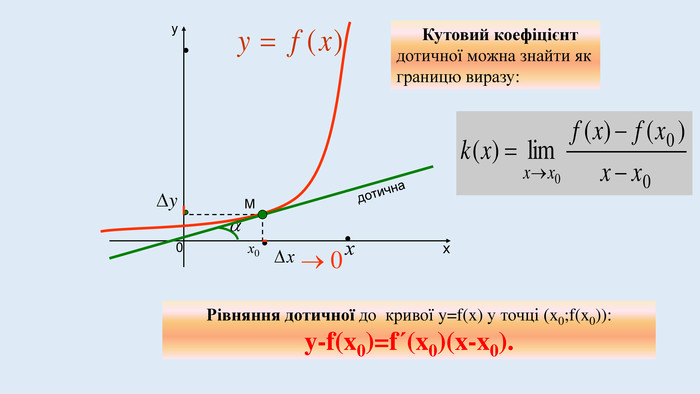
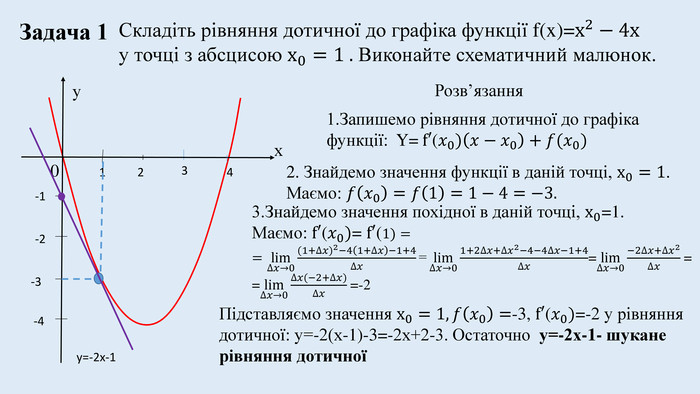
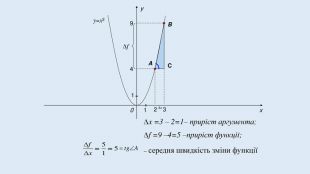
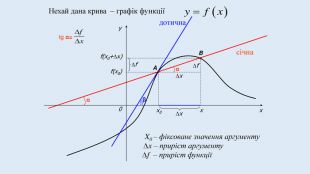
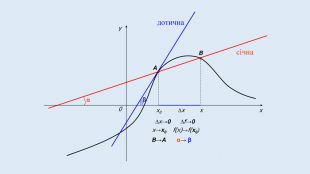
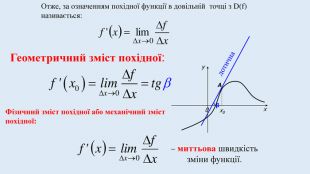
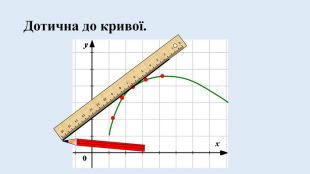
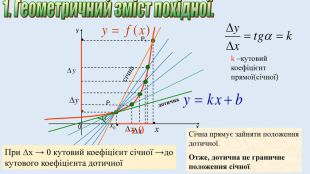
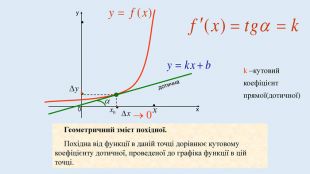
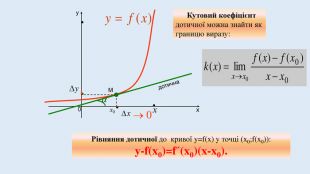
Цю презентацію можна використати для ознайомлення учнів з означенням похідної, з геометричним та механічним змістом похідної.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Лаконічно, доступно, все є. Дякую!


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку