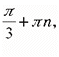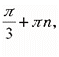ЗОВНІШНЄ НЕЗАЛЕЖНЕ ОЦІНЮВАННЯ – 2008 ТЕСТ ІЗ MAТЕМАТИКИ Час виконання – 180 хвилин Тест складається з трьох частин, що містять 36 завдань різних форм. Відповіді на завдання Частини 1 та Частини 2 Ви маєте позначити в бланку А. Розв’язання завдань Частини 3 слід записати у бланку Б. Правила виконання подано перед завданнями кожної нової форми. Інструкція щодо роботи в тестовому зошиті 1.     Відповідайте тільки після того, як Ви уважно прочитали та зрозуміли завдання. 2.     У разі необхідності використовуйте як чернетку вільні від тексту місця в зошиті. 3.     Намагайтеся виконати всі завдання. Інструкція щодо заповнення бланків відповідей А і Б 1.      До бланків записуйте лише правильні, на Вашу думку, відповіді. 2.      Відповіді вписуйте акуратно, дотримуючись вимог інструкції до кожноїформи завдань. 3.      Неправильно позначені, закреслені та підчищені відповіді в бланку А – це ПОМИЛКА! 4.      Якщо Ви записали відповідь неправильно, можете виправити її у відповідномумісці бланка А. 5.      Виконавши завдання Частини 3, запишіть їх розв’язання в бланку Б. 6.      Ваш результат залежатиме від загальної кількості правильних відповідей,записаних у бланку А, та розв’язання завдань Частини 3. 7.      Позначте номер Вашого зошита у відповідному місці бланка А та бланка Б. Ознайомившись з інструкцією, перевірте якість друку зошита та кількість сторінок. Їх має бути 24. Бажаємо Вам успіху!

ЗОШИТ

1

© Український центр оцінювання якості освіти, 2008

Частина 1

Завдання 1-25 мають по п’ять варіантів відповіді, з яких лише ОДИН ПРАВИЛЬНИЙ. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А. Не робіть інших позначок, тому що комп’ютерна програма реєструватиме їх як ПОМИЛКИ.

1.   Знайдіть натуральне, одноцифрове число N, якщо відомо, що сума 510+N ділиться на 9 без остачі.

А	Б	В	Г	Д
1	3	5	6	9

2.   Визначте кількість усіх дробів із знаменником 28, які більші за, але менші від

А	Б	В	Г	Д
шість	чотири	три	два	один

4. Розв’яжіть нерівність > 0.

А	Б		В	Г	Д
(; 5)(8; )	(; 5)(5; )		(5; 8)	(5; )	(; 5)
5. Якщо	і R > 0, то R =
А	Б		В	Г	Д

2

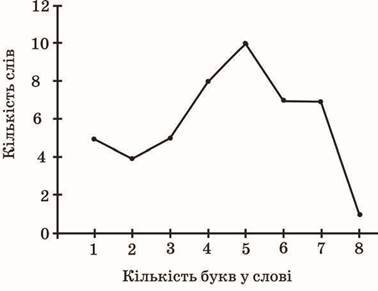
6. В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода   це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот.

А	Б	В	Г	Д
2	4	5	8	10
7. Укажіть правильну нерівність
А	Б	В	Г	Д
b < a < c	a < b < c	c < a < b	a< c < b	b < c < a

8.   Обчисліть                       

А	Б	В	Г	Д
1				Інша відповідь

9.   Укажіть найменший додатний період функції                        

А	Б	В	Г	Д

4

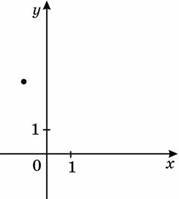
10.              На рисунку зображено точку, через яку проходить графік функції y=f(x). Укажіть функцію f(x) . 

А	Б	В	Г	Д

А	Б	В	Г	Д
		3		4

13.   Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2, 3, 4, 5, 6, 7, 8, 9.

А	Б	В	Г	Д
28	56	70	112	Інша відповідь

14.   Розв’яжіть нерівність

А	Б	В	Г	Д
(5; 0)	(0; 5)	(5; +)	( 0,5; 5)	(; 5)

6

15.   Укажіть корінь рівняння                            який  належить проміжку (2; 1].

А	Б	В	Г	Д

16.   Розв’яжіть рівняння:

А	Б	В	Г	Д
рівняння не має коренів	x = 1	x =  0,5	x = 0,5	x = 1
17. Укажіть область значень фун		кції
А	Б	В	Г	Д
[9; +)	[0; )	[3; +)	[3; +)	(; +)

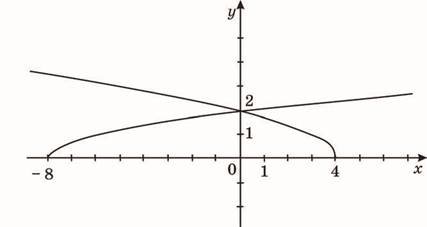
18.   На рисунку зображено графіки функцій                              і

Укажіть проміжок, на якому виконується нерівність f(x)  g(x).

А	Б	В	Г	Д
(; 0]	[8; )	[0; )	[0; 4]	[8; 0]

8

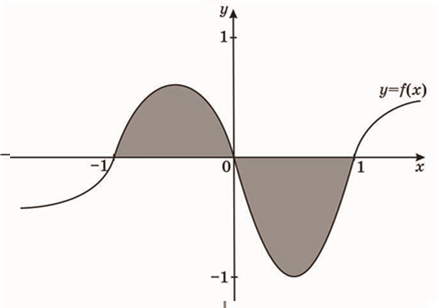
19.   На рисунку зображено графік функції  y=f(x) . Укажіть формулу для обчислення площі зафарбованої фігури.

А	Б		В			Г		Д
1 yf(x)dx – 1	0                                    1 yf(x)dx  yf(x)dx – 1                                       0		1                                           0 yf(x)dx  yf(x)dx 0                                        –1			0 2 yf(x)dx –1		1 2 yf(x)dx 0
А		Б		В		Г		Д
1		0,5		0		0,5		1

21. Тіло рухається прямолінійно за законом                        (час t вимірюється в секундах, шлях s  в метрах). Визначте прискорення його руху в момент  t = 10 c.

А	Б	В	Г	Д
164 м/с2	60 м/с2	36 м/с2	20 м/с2	10 м/с2
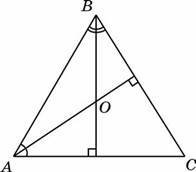
22. У трикутник що перетинають	у АВС A = 59c, ся в точці О. Виз	B = 62c. Із вер начте величину	шин цих кутів п кута АОВ.	роведено висоти,
А	Б	В	Г	Д
98c	121c	144c	149c	154c

10

23.              Сторони трикутника, одна з яких на 8 см більша за другу, утворюють кут 120c, а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.

А	Б	В	Г	Д
84 см	72 см	64 см	60 см	56 см

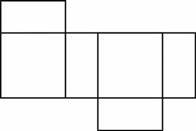
24.              На рисунку зображено розгортку поверхні тіла, складеного з двох квадратів і чотирьох однакових прямокутників, довжина сторін яких  3см і 6см. Визначте об’єм цього тіла.

А	Б	В	Г	Д
1:	2:	1:2	2:3	1:3

12

Частина 2

Розв’яжіть завдання 26-33. Запишіть відповідь у зошит і бланк А.

26.   Обчисліть

Відповідь ___________________

27.   Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої b_n=5H3^–n.

Відповідь ___________________

28.   Розв’яжіть рівняння                                                       Якщо   рівняння   має   кілька коренів, то у відповідь запишіть їх добуток.

Відповідь ___________________

29.   Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому  0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому   0,34.

Відповідь ___________________

30.   У коробці є 80 цукерок, з яких 44  з чорного шоколаду, а решта  з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду.

У відповідь запишіть їх суму.

Відповідь ___________________

32.   Визначте кут між векторами       і              у градусах, якщо відомо, що

Відповідь ___________________

33.   На рисунку зображено розгортку конуса. Визначте відношення площі повної поверхні цього конуса до площі його бічної поверхні.

Відповідь ___________________

Частина 3

Розв’язання завдань 34-36 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, спираючись на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань схемами, графіками, таблицями.

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

34.   У правильній трикутній піраміді SABC з основою АВС бічне ребро вдвічі більше за сторону основи. Точки K і L є серединами ребер АС і ВС відповідно. Через пряму KL, паралельно до ребра SС, проведено площину α. Знайдіть кут  між площиною α і площиною (АВС).

ЧЕРНЕТКА

35.   Розв’яжіть систему нерівностей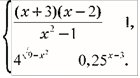

ЧЕРНЕТКА

22

36.   Задано функцію

1.   Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2.   Побудуйте ескіз графіка функції f(x).

3.   Знайдіть кількість коренів рівняння f(x) = a , де aXR, залежно  від значення     параметра а. 

ЧЕРНЕТКА

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

Кінець тестового зошита

24

ЗОВНІШНЄ НЕЗАЛЕЖНЕ ОЦІНЮВАННЯ – 2008 ТЕСТ ІЗ MAТЕМАТИКИ Час виконання – 180 хвилин Тест складається з трьох частин, що містять 36 завдань різних форм. Відповіді на завдання Частини 1 та Частини 2 Ви маєте позначити в бланку А. Розв’язання завдань Частини 3 слід записати у бланку Б. Правила виконання подано перед завданнями кожної нової форми. Інструкція щодо роботи в тестовому зошиті 1.     Відповідайте тільки після того, як Ви уважно прочитали та зрозуміли завдання. 2.     У разі необхідності використовуйте як чернетку вільні від тексту місця в зошиті. 3.     Намагайтеся виконати всі завдання. Інструкція щодо заповнення бланків відповідей А і Б 1.      До бланків записуйте лише правильні, на Вашу думку, відповіді. 2.      Відповіді  вписуйте  акуратно,  дотримуючись  вимог  інструкції  до  кожної форми завдань. 3.      Неправильно позначені, закреслені та підчищені відповіді в бланку А – це ПОМИЛКА! 4.      Якщо Ви записали відповідь неправильно, можете виправити її у відповідному місці бланка А. 5.      Виконавши завдання Частини 3, запишіть їх розв’язання в бланку Б. 6.      Ваш результат залежатиме від загальної кількості правильних відповідей,записаних у бланку А, та розв’язання завдань Частини 3. 7.      Позначте номер Вашого зошита у відповідному місці бланка А та бланка Б. Ознайомившись з інструкцією, перевірте якість друку зошита та кількість сторінок. Їх має бути 24. Бажаємо Вам успіху!

ЗОШИТ

2

© Український центр оцінювання якості освіти, 2008

Частина 1

Завдання 1-25 мають по п’ять варіантів відповіді, з яких лише ОДИН ПРАВИЛЬНИЙ. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А. Не робіть інших позначок, тому що комп’ютерна програма реєструватиме їх як ПОМИЛКИ.

1.   Укажіть правильну нерівність, якщо

А	Б	В	Г	Д
b < c < a	a < c < b	c < a < b	a < b < c	b < a < c

2.   Укажіть найменший додатний період функції                        

А	Б	В	Г	Д

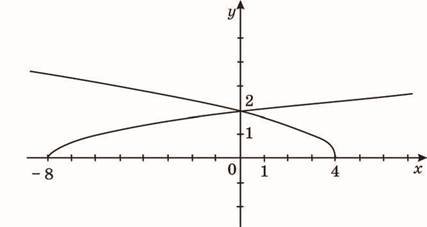
4. На  рисунку  зображено графіки функцій                              і

Укажіть проміжок, на якому виконується нерівність f(x)  g(x).

А	Б	В	Г	Д
[8; 0]	[0; 4]	[0; )	[8; )	(; 0]

2

5.   Обчисліть                       

А	Б	В	Г	Д
				Інша відповідь

6.   На рисунку зображено точку, через яку проходить графік функції y=f(x). Укажіть функцію f(x) . 

А	Б	В	Г	Д
9	6	5	3	1

8.   Якщо                         і R > 0, то R =

А	Б	В	Г	Д

9.   Визначте кількість усіх дробів із знаменником 28, які більші за, але менші від

А	Б	В	Г	Д
один	два	три	чотири	шість

4

А	Б	В	Г	Д
[3; +)	[3; +)	[0; )	[9; +)	(; +)

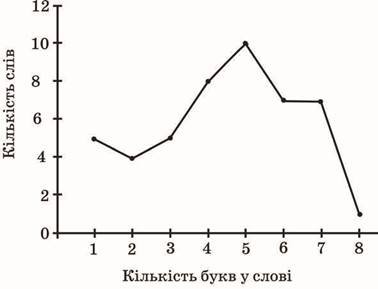
10.              В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода   це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот.

А	Б	В	Г	Д
2	4	5	10	8

.

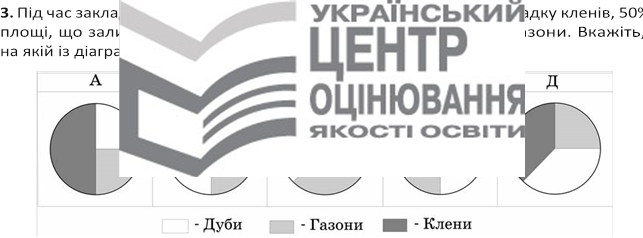
12.   Під час закладання нового парку 25% його площі відвели під посадку кленів, 50% площі, що залишилася,  під посадку дубів, а решту площі  під газони. Вкажіть, на якій із діаграм правильно показано розподіл посадок:

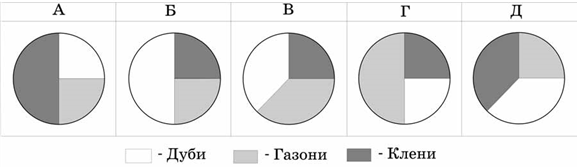
13.   Укажіть область значень функції

14.   Знайдіть значення виразу                            , якщо a = 2,5.

А	Б	В	Г	Д
1	1	0	0,5	0,5

А	Б	В	Г	Д
164 м/с2	60 м/с2	36 м/с2	20 м/с2	10 м/с2

А	Б		В	Г	Д
112	Інша відповідь		70	56	28
18. Розв’яжіть н	ерівність	> 0.
А	Б		В	Г	Д
(; 5)(5; )	(; 5)(8; )	(; 5)		(5; )	(5; 8)

15.   Розв’яжіть рівняння                       

А	Б	В	Г	Д
nXZ	nXZ	nXZ	nXZ	nXZ

19.   Тіло рухається прямолінійно за законом                       (час t вимірюється в секундах, шлях s  в метрах). Визначте прискорення його руху в момент  t = 10 c.

20.   Розв’яжіть нерівність

А	Б	В	Г	Д
(0; 5)	( 0,5; 5)	(5; +)	(5; 0)	(; 5)

А	Б	В	Г	Д
154c	149c	144c	121c	98c

21.   На рисунку зображено графік функції  y=f(x) . Укажіть формулу для обчислення площі зафарбованої фігури. а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.

А	Б	В	Г	Д
56 см	60см	64 см	72 см	84 см

23.              У трикутнику АВС A = 59c, B = 62c. Із вершин цих кутів проведено висоти, що перетинаються в точці О. Визначте величину кута АОВ.

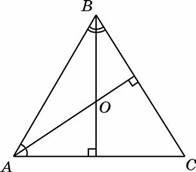
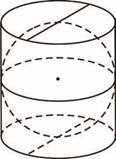
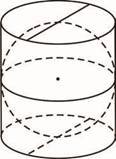
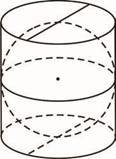
24.              У склянку циліндричної форми, наповнену водою по самі вінця, поклали металеву кульку, що дотикається до дна склянки та стінок (див. рисунок). Визначте відношення об’єму води, яка залишилась у склянці, до об’єму води, яка вилилася зі склянки.

А	Б	В	Г	Д
1:	2:	1:2	2:3	1:3

25.              На рисунку зображено розгортку поверхні тіла, складеного з двох квадратів і чотирьох однакових прямокутників, довжина сторін яких   3см і 6см. Визначте об’єм

А	Б	В	Г	Д
Інша відповідь	36 см3	144 см3	54 см3	108 см3

Частина 2

Розв’яжіть завдання 26-33. Запишіть відповідь у зошит і бланк А.

26.              Розв’яжіть рівняння                                                       Якщо   рівняння   має   кілька коренів, то у відповідь запишіть їх добуток.

Відповідь ___________________

27.              У коробці є 80 цукерок, з яких 44  з чорного шоколаду, а решта  з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду.

Відповідь ___________________ 28. Обчисліть

Відповідь ___________________

14

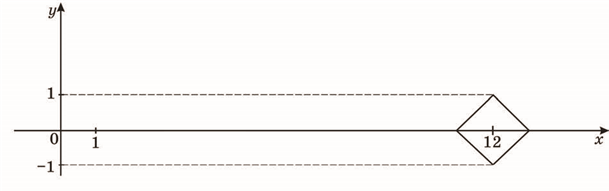
29.   Використовуючи графік рівняння                               (див. рисунок), знайдіть  усі значення параметра а, при яких система                                     має єдиний розв’язок.

У відповідь запишіть їх суму.

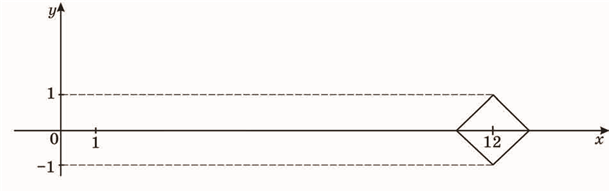
Відповідь ___________________

30.   Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої            b_n=5H3^–n.

Відповідь ___________________

31.   Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому  0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому   0,34.

Відповідь ___________________

17

32.   На рисунку зображено розгортку конуса. Визначте відношення площі повної поверхні цього конуса до площі його бічної поверхні.

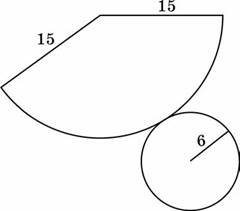
Відповідь ___________________

Відповідь ___________________

Частина 3

Розв’язання завдань 34-36 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, спираючись на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань схемами, графіками, таблицями.

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

34.   У правильній трикутній піраміді SABC з основою АВС бічне ребро вдвічі більше за сторону основи. Точки K і L є серединами ребер АС і ВС відповідно. Через пряму KL, паралельно до ребра SС, проведено площину α. Знайдіть кут  між площиною α і площиною (АВС).

ЧЕРНЕТКА

35.   Розв’яжіть систему нерівностей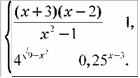

ЧЕРНЕТКА

22

36.   Задано функцію                    

1.   Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2.   Побудуйте ескіз графіка функції f(x).

3.   Знайдіть кількість коренів рівняння f(x) = a , де  aXR, залежно  від значення     параметра а. 

ЧЕРНЕТКА

23

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

Кінець тестового зошита

24

ЗОВНІШНЄ НЕЗАЛЕЖНЕ ОЦІНЮВАННЯ – 2008 ТЕСТ ІЗ MAТЕМАТИКИ Час виконання – 180 хвилин Тест складається з трьох частин, що містять 36 завдань різних форм. Відповіді на завдання Частини 1 та Частини 2 Ви маєте позначити в бланку А. Розв’язання завдань Частини 3 слід записати у бланку Б. Правила виконання подано перед завданнями кожної нової форми. Інструкція щодо роботи в тестовому зошиті 1.     Відповідайте тільки після того, як Ви уважно прочитали та зрозуміли завдання. 2.     У разі необхідності використовуйте як чернетку вільні від тексту місця в зошиті. 3.     Намагайтеся виконати всі завдання. Інструкція щодо заповнення бланків відповідей А і Б 1.      До бланків записуйте лише правильні, на Вашу думку, відповіді. 2.      Відповіді  вписуйте  акуратно,  дотримуючись  вимог  інструкції  до  кожної форми завдань. 3.      Неправильно позначені, закреслені та підчищені відповіді в бланку А – це ПОМИЛКА! 4.      Якщо Ви записали відповідь неправильно, можете виправити її у відповідному місці бланка А. 5.      Виконавши завдання Частини 3, запишіть їх розв’язання в бланку Б. 6.      Ваш результат залежатиме від загальної кількості правильних відповідей,записаних у бланку А, та розв’язання завдань Частини 3. 7.      Позначте номер Вашого зошита у відповідному місці бланка А та бланка Б. Ознайомившись з інструкцією, перевірте якість друку зошита та кількість сторінок. Їх має бути 24. Бажаємо Вам успіху!

ЗОШИТ

3

© Український центр оцінювання якості освіти, 2008

Частина 1

Завдання 1-25 мають по п’ять варіантів відповіді, з яких лише ОДИН ПРАВИЛЬНИЙ. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А. Не робіть інших позначок, тому що комп’ютерна програма реєструватиме їх як ПОМИЛКИ.

1. Знайдіть значення виразу                            , якщо a = 2,5.

А	Б			В	Г	Д
1	0,5			0	0,5	1
2. Розв’яжіть не	рівність	<
А	Б			В	Г	Д
(5; 0)	(0; 5)			(5; +)	( 0,5; 5)	(; 5)
3. Розв’яжіть рі	вняння:
А	Б			В	Г	Д
рівняння не має коренів	x = 1			x =  0,5	x = 0,5	x = 1

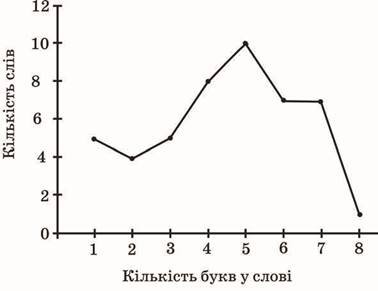
4.   В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода   це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот.

А	Б	В	Г	Д
2	4	5	8	10

2

3

А	Б	В	Г	Д
(; 0]	[8; )	[0; )	[0; 4]	[8; 0]

5.   Обчисліть                       якщо                        

А	Б				В	Г		Д
					3			4
6. Розв’яжіть не	рівність                 > 0.
А		Б			В	Г	Д
(; 5)(8;	)	(; 5)			(5; 8)	(5; )	(; 5)(5; )
7. Укажіть обла	сть значень функції
А		Б			В	Г		Д
[9; +)		[0; )			[3; +)	[3; +)		(; +)

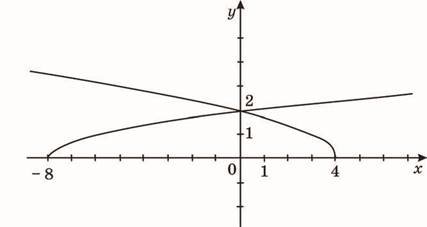
9. На рисунку зображено графіки функцій                              і    

Укажіть проміжок, на якому виконується нерівність f(x)  g(x).

А	Б	В	Г	Д

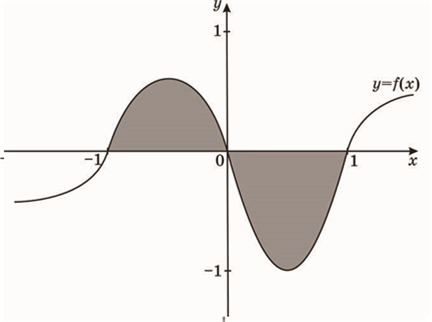
10. На рисунку зображено графік функції  y=f(x) . Укажіть формулу для обчислення площі зафарбованої фігури.

А	Б	В	Г	Д

.

12.   Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2, 3, 4, 5, 6, 7, 8, 9.

А	Б	В	Г	Д
28	56	70	112	Інша відповідь

13.   Якщо                         і R > 0, то R =

14.   Обчисліть                       

А	Б	В	Г	Д
1				Інша відповідь

А	Б	В	Г	Д

15.   Розв’яжіть рівняння                       

А	Б	В	Г	Д
nXZ	nXZ	nXZ	nXZ	nXZ

17.   Укажіть правильну нерівність, якщо

А	Б	В	Г	Д
b < a < c	a < b < c	c < a < b	a< c < b	b < c < a

18.   Укажіть найменший додатний період функції                        

А	Б	В	Г	Д
108 см3	54 см3	144 см3	36 см3	Інша відповідь

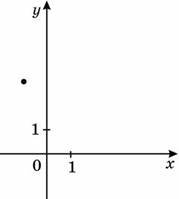
19.   На рисунку зображено точку, через яку проходить графік функції y=f(x). Укажіть функцію f(x) . 

А	Б	В	Г	Д

20.   Знайдіть натуральне, одноцифрове число N, якщо відомо, що сума 510+N ділиться на 9 без остачі.

21.   Тіло рухається прямолінійно за законом                       (час t вимірюється в секундах, шлях s  в метрах). Визначте прискорення його руху в момент  t = 10 c.

А	Б	В	Г	Д
164 м/с2	60 м/с2	36 м/с2	20 м/с2	10 м/с2

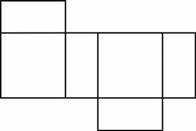
22.   На рисунку зображено розгортку поверхні тіла, складеного з двох квадратів і чотирьох однакових прямокутників, довжина сторін яких  3см і 6см. Визначте об’єм цього тіла.

23.   У склянку циліндричної форми, наповнену водою по самі вінця, поклали металеву кульку, що дотикається до дна склянки та стінок (див. рисунок). Визначте відношення об’єму води, яка залишилась у склянці, до об’єму води, яка вилилася зі склянки.

А	Б	В	Г	Д
2:	1:	1:2	1:3	2:3

24.   У трикутнику АВС A = 59c, B = 62c. Із вершин цих кутів проведено висоти, що перетинаються в точці О. Визначте величину кута АОВ.

А	Б	В	Г	Д
121c	98c	144c	149c	154c

25.   Сторони трикутника, одна з яких на 8 см більша за другу, утворюють кут 120c, а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.

А	Б	В	Г	Д
64 см	72 см	84 см	60 см	56 см

Частина 2

Розв’яжіть завдання 26-33. Запишіть відповідь у зошит і бланк А.

26. Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому  0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому   0,34.

Відповідь ___________________

Відповідь ___________________

28.   Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої b_n=5H3^–n.

Відповідь ___________________

14

29.   Обчисліть

Відповідь ___________________

30.   На рисунку зображено розгортку конуса. Визначте відношення площі повної поверхні цього конуса до площі його бічної поверхні.

Відповідь ___________________

31.   Визначте кут між векторами       і              у градусах, якщо відомо, що

Відповідь ___________________

16

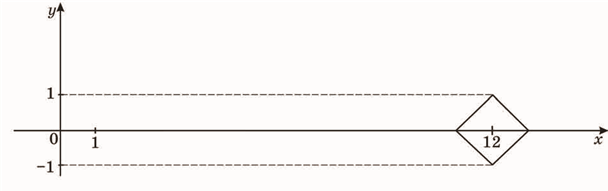
32.   Використовуючи графік рівняння                               (див. рисунок), знайдіть  усі значення параметра а, при яких система                                     має єдиний розв’язок.

У відповідь запишіть їх суму.

Відповідь ___________________

шоколаду.

Відповідь ___________________

Частина 3

Розв’язання завдань 34-36 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, спираючись на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань схемами, графіками, таблицями.

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

34.   У правильній трикутній піраміді SABC з основою АВС бічне ребро вдвічі більше за сторону основи. Точки K і L є серединами ребер АС і ВС відповідно. Через пряму KL, паралельно до ребра SС, проведено площину α. Знайдіть кут  між площиною α і площиною (АВС).

ЧЕРНЕТКА

35.   Розв’яжіть систему нерівностей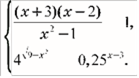

ЧЕРНЕТКА

36.   Задано функцію                    

1.   Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2.   Побудуйте ескіз графіка функції f(x).

3.   Знайдіть кількість коренів рівняння f(x) = a , де  aXR, залежно  від значення     параметра а. 

ЧЕРНЕТКА

УВАГА! Розв’язання завдань 34-36 запишіть у бланку Б.

Кінець тестового зошита

 

 

ВІДПОВІДІ НА ЗАВДАННЯ ТЕСТУ З МАТЕМАТИКИ

 

(Затверджені експертною комісією Українського центру оцінювання якості освіти 

                                                                                                            29 квітня 2008 року) 

Частина 1

 

Завдання 1-25 мають по п’ять варіантів відповіді, з яких лише 

ОДИН ПРАВИЛЬНИЙ.

 

1. Завдання:  Знайдіть натуральне, одноцифрове число N, якщо відомо, що сума 510+N ділиться на  9 без остачі.

 

Відповідь: 3

Бевз Г.П. Математика: 6 кл. : Підручник для загальноосвіт. навч. закл. /Г.П.Бевз, В.Г.Бевз. ─ К.: Генеза, 2006 ─ С. 15.

 

2. Завдання: Визначте кількість усіх дробів із знаменником 28, які більші за  , але менші

 

Відповідь: чотири

 

 

на якій із діаграм правильно показано розподіл посадок.

 

Відповідь: 

 

 

Янченко Галина, Кравчук Василь. Математика: Підручник для 6 класу. ─ Тернопіль: Підручники і посібники, 2006 ─ С.149

 

^{х2 +} 64

4. Завдання: Розв’яжіть нерівність > 0. х −5

Відповідь: (5; +∞)

Бевз Г.П. Алгебра: Підручник для 9 кл.загальноосвіт. навч. закладів. ─ К.: Освіта, 2006 ─ С. 21.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підруч. для 11 кл. загально освіт. навч. закладів. – К.: Зодіак – ЕКО, 2003. − С. 362.

 

 

GMm

5. Завдання: ЯкщоF=               і R> 0 , то R =

Відповідь: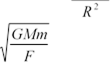

 

Бевз Г.П. Алгебра: Підруч. для 8 кл. загальноосвіт. навч. закл. ─ К.: Освіта, 2004 ─ С. 55.

 

 

6.  Завдання: В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода − це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот. 

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11  класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2005. – С. 329.

Бевз Г.П. Алгебра: Підручник для 9 кл. загальноосвітніх навчальних закладів. –К.: Освіта, 2006. − С. 92.

 

7.  Завдання: Укажіть правильну нерівність, якщо a=5 2 ; b=7 ; c = 51.

 

Відповідь: b a c< <

 

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10  класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004 – С.262.

 

8.  Завдання: Знайдіть значення виразу cos^{4 π}−sin⁴              .

12

3

Відповідь: 

2

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С. 96.

 

9.  Завдання: Знайдіть найменший додатний період функції у = 2ctg(3 )x .

Відповідь:  

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С. 48.

 

 

10.              Завдання: На рисунку зображено точку, через яку проходить графік функції y = f x( ) . Укажіть функцію f ( )x .

 

 

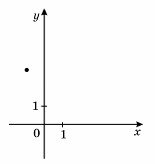
Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.173.

 

 

    12. Завдання: Обчисліть log_a ab , якщо log_a b = 7 .

 

Відповідь: 4

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С.224.

 

 

13. Завдання: Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2, 3, 4, 5, 6, 7, 8, 9.

 

Відповідь: 28

 

Бевз Г.П. та інші. Геометрія: Підручник для 10 − 11 кл. загальноосвітніх навчальних закладів. – К.: Вежа, 2004. − С.183.

 

14. Завдання: Розв’яжіть нерівність log_0,5 5 < log_0,5 x .

 

Відповідь: (0; 5)

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − 234 с.

 

15. Завдання: Укажіть корінь рівняння х² − 6х = 9, який належить проміжку (− 2; 1]. 

Відповідь: 3−3 2

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.5.

16. Завдання: Розв’яжіть рівняння: 3^x ₌ ^{2 3} .

6

Відповідь: x =−0,5

 

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.338.

 

 

 

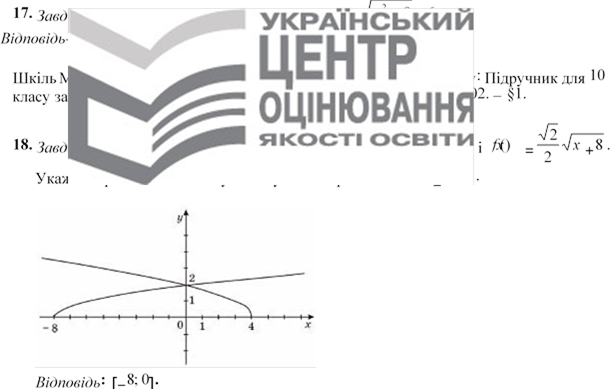
19. Завдання: На рисунку зображено графік функції y = f x( ) . Укажіть формулу для обчислення площі зафарбованої фігури.

 

 

 

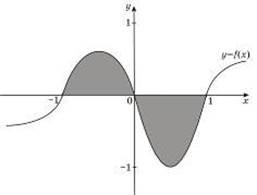
                                  0                                 1

      Відповідь: ∫ f x dx( ) −∫ f x dx( )        

                                  −1                               0

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С. 143. Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11  класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2005. – С. 209.

 

9+ −а² 6а

20. Завдання: Знайдіть значення виразу         , якщо а = 2,5.  а−3

Відповідь: −1

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для

10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. −С.139.

 

2 ³ 2t² + 4t (час t 21. Завдання: Тіло рухається прямолінійно за законом s t( ) = t − 3

вимірюється в секундах, шлях  s ─ в метрах). Визначте прискорення його руху в момент t =10 .c

 

Відповідь: 36 м /c²

 

Бевз Г.П. та інші. Геометрія: Підручник для 10 − 11 кл. загальноосвітніх навчальних закладів. – К.: Вежа, 2004. − С.138-139.

 

22.  Завдання: У трикутнику АВС ∠А= 59°,  ∠В= 62° . Із вершин цих кутів проведено висоти, що перетинаються в точці О. Визначте величину кута АОВ.

 

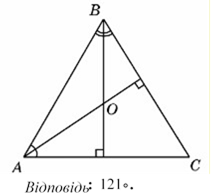
Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 7-9 кл. загально освіт. навч закл.-К.:

Школяр, 2004. – С.53

 

23.  Завдання: Сторони трикутника, одна з яких на 8 см більша за другу, утворюють        кут 120°, а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.

 

Відповідь: 60 см .

 

Бевз Г.П. та інші. Геометрія: Підручник для 7 − 9 кл. загальноосвітніх навчальних закладів. – К.: Вежа, 2004. − С.194-195

 

24.  Завдання: На рисунку зображено розгортку поверхні тіла, складеного з двох квадратів і чотирьох однакових прямокутників, довжина сторін яких ─ 3см і 6 см. Визначте об’єм цього тіла. 

склянки.

 

 

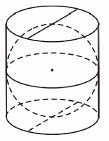
Відповідь: 1:2

 

Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10 - 11 кл. серед.школ.-К.: Освіта,1994. – С.113, 115.

 

 

 

 

 

 

 

 

 

ЧАСТИНА 2

 

26. Завдання: Обчисліть 2 13cos(arctg ) .

            Відповідь: 6

 

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.153.

 

27. Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої b_п = 5 3⋅ ^−п .

             

Відповідь: 2,5

 

 

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. –       С.74.

28.   Завдання: Розв’яжіть рівняння х− +5        2х² −14х+ =13           0.

      Якщо рівняння має кілька коренів, то у  відповідь запишіть їх добуток.

 

Відповідь: −2.

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для

10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. −С.158.

 

29.   Завдання: Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому − 0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 

      50 кілограмів, концентрація солі в якому − 0,34.

 

Відповідь: 10.

 

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. –  С.94-98.

 

30.   Завдання: У коробці 80 цукерок, з яких 44 − з чорного шоколаду, а решта − з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду.

 

Відповідь: 0,45.

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.230.

 

 

31.   Завдання: Використовуючи графік рівняння у = − −1 х 12 (див. рисунок), знайдіть

^⎪⎧ x−12 + y =1,

усі значення параметра а, при яких система ^⎨⎩⎪(x−a)₂ + y_{2 =} 4 має єдиний розв’язок.

У відповідь запишіть їх суму. 

 

Відповідь: 48.

 

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. –   С.49.

                                                                                   r     r    r

32. Завдання: Визначте кут між векторами a і b c+ у градусах, якщо відомо, що ρ          ρ            ρ а (2; 2), в (2; 4) і с ( 2; 6−  − ) .

 

Відповідь: 135.

 

Відповідь: 1,4

 

Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10 - 11 кл. серед.школ.-К.:

Освіта,1994. – С.117.

 

 

ЧАСТИНА ІІІ

 

Розв’язання завдань 34-36 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, спираюись на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань схемами графіками, таблицями.

 

 

34.  Завдання: У правильній трикутній піраміді SABC з основою АВС бічне ребро вдвічі більше за сторону основи. Точки K і L є серединами ребер АС і ВС відповідно. Через пряму KL, паралельно до ребра SС, проведено площину α . Знайдіть кут ϕ між площиною α і площиною (АВС). 

 

1

Відповідь: ϕ= arccos.

2 3

Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10 - 11 кл. серед.школ.-К.: Освіта,1994. – С.12, 50.

 

^⎪⎧(x+x3)(² −x¹−2) ^≤1,

35.  Завдання: Розв’яжіть систему нерівностей  _⎨

⎪⎩4 9−x2 ≤ 0,25x−3.

 

             Відповідь: x∈ − − ∪[ 3; 1) {3}.   

 

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.232, 308, 351.

 

36.  Завдання: Задано функцію  f ( )x = 3x⁴ −4x³ −12x² . 

1.  Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2.  Побудуйте ескіз графіка функції f ( )x .

3.  Знайдіть кількість коренів рівняння f ( )x = a , де a R∈ , залежно від значення                 параметра  а.

 

Відповідь: 3. Якщо a∈ −∞ −( ; 32) рівняння не має коренів;      якщо a=−32 рівняння має один корінь;      якщо a∈ − − ∪ +∞( 32; 5) (0; ) рівняння  має два кореня;      якщо a=−5 та при a=0 рівняння  має три кореня;      якщо a∈ −( 5;0) рівняння має чотири кореня.

 

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.112.