Урок "Формули скороченого множення"

АЛГЕБРА,   7  КЛАС 

Яненко Юлія Володимирівна

учитель математики « Троїцького ліцею Троїцької селищної ради Троїцького району Луганської області»

ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ.

Мета уроку: вивести формулу квадрат тричлена та куб двочлена; удосконалити вміння і навички підносити двочлен до куба;  дослідити залежність між коефіцієнтами двочлена з нульовим та  натуральним показником; формувати математичну,комунікативну, соціальну компетентності та уміння вчитися впродовж життя; виховувати наполегливість, самостійність, толерантність.

Тип уроку: урок-дослідження.

Обладнання: проектор, екран , аркуші ватману, фломастери, сигнальні картки.

ХІД УРОКУ:

І. Організаційний етап.Мотивація навчальної діяльності.

Вступне слово учителя.Дорогі діти!  Сьогодні ми проведемо незвичайний урок. Епіграфом до нашого уроку я обрала слова Анрі  Пуанкаре«За допомогою логіки – доводять, за допомогою інтуїції – винаходять». Ми вивчили формулу квадрат двочлена. Навчилися застосовувати ці формули до спрощення виразів, доведення тотожностей, розв’язування рівнянь. Але сьогодні ми спробуємо розширити наші знання про формули скороченого множення. Зовсім недавно у нас в ліцеї проходив веселковий тиждень, то я вирішила і наш урок прикрасити райдужними кольорами.Будемо працювати  в групах . Кожна група має свій колір.Кожен з вас має сигнальні картки такого ж кольору.Я за собою залишаю червоний колір. За правильні відповіді ви будете отримувати червоні смужки, які потім переведемо у бали. У групі є консультант, який буде допомагати мені.

Весе́лка, також ра́йдуга— оптичне явище в атмосфері, що являє собою одну, дві чи декілька різнокольорових дуг, що спостерігаються на тлі хмари, якщо вона розташована проти Сонця.  Веселка складається з 7 -ми кольорів (червоний, оранжевий, жовтий, зелений, блакитний, синій, фіолетовий), які плавно переходять один в один. Веселка з’являється при висвітленніСонцембезлічіводянихкрапель (абодощу, або туману). Точніше, сонячне світло переломлюється відбивається крапельками води. Веселку можна побачити, якщоСонцез находиться вище 42 градусів над горизонтом. Веселка з’являється не тільки при сонячномуосвітленні але й при місячному освітленні. Вогняна веселка на відміну відзвичайної з’являється лише тоді, коли в небі є перисті хмари і Сонце знаходиться вище 58 градусів над горизонтом. Іноді веселки з’являються в декількох формах. Чотириразова веселка у природі зустрічається дуже рідко. В африканських народів існує повір’я: де веселка торкається Землі, там можна знайти скарб (дорогоцінне каміння). Веселка є невловимою, до неї неможливо підійти або фізично торкнуться. Ісаак Ньютон визначив 7 кольорів видимого спектру, які разом складають біле світло. У міфології веселка — символ посередництва між небом і землею. Вірування в веселку, що п'є воду, відбилося і в Шевченка:

Розкажи, як за горою сонечкосідає.
         Як у Дніпра, веселочка воду позичає

ІІ. Актуалізація опорних знань.

 Виконання усних вправ.

Завдання проектується на екран. Учні мають сигнальні картки з номерами 1,2,3,4.По команді вчителя піднімають сигнальну картку з номером правильної відповіді.

І.Який з виразів є квадратом суми:

1.а²+в² ; 2.с+5; 3.(t+m)²; 4.x²+4  ?

Відповідь:3

ІІ.Який з виразів є квадратом різниці:

1.(а-5)³; 2.(3-n)²; 3.с²-d²  4.t²-4?

Відповідь: 2

ІІІ. Встановіть відповідність (по команді вчителя кожен учень піднімає  сигнальну картку з номером, який відповідає формулі):

А) (а+в)²=	1.1-2в+в²
Б)(х-у) ² =	2.а²+4а+4
В)(а+2) ²=	3.а²+2ав+в²
Г)(1-в) ²=	4.х²-2ху+у²

Відповіді: А-3;Б-4;В-2;Г-1.

ІV. Які з рівностей є правильними:

1.(m-3)²=m²-6m+3²

2. (p+7)²=p²+7²

3. (2-a)²=2²-2a+a²

4. (в+3)²=в²+6в+3?

Відповідь: 1

ІІІ. Вивчення нового матеріалу.

         «Найкращий спосіб вивчити що-небудь – це відкрити самому».

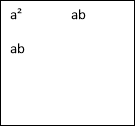
Ще Евклід знав прийом піднесення до квадрату суми двох доданків, який і ми сьогодні з вами вивчаємо. Правда трактував він це з геометричної точки зору(слайд).

 

 

 

 

 a b

 a     (a+b)²=a²+2ab+b².

 

 

 

 b

 

Але чому тільки квадрат двох чисел? І чому тільки до квадрату? А чи не можна знайти метод піднесення до третього, четвертого і більш високих степенів ?

На аркуші А-3 накресліть квадрат і спробуйте записати формулу квадрата суми трьох чисел.(a+b+c)²

Відповідь:(a+b+c)²=a²+b²+c²+2ab+2ac+2bc.

 

 

 

 

А давайте виведемо цю формулу з точки зору алгебри, кажуть, аналітично.

Відповідь: 

(a+b+c)²=(a+b+c)(a+b+c)=a²+ab+ac+ab+b²+bc+ac+bc+c²=                 =a²+b²+c²+2ab+2ac+2cb.

 Отже, квадрат тричлена дорівнює сумі квадратів всіх виразів і подвоєних добутків всіх можливих пар цих виразів.

 А тепер , будь ласка,запропонуйте спосіб піднесення двочлена до кубу (учні працюють в групах, хто впорався із завданням сигналізує карткою).

Відповідь:  (a+b)³=(a+b)²(a+b)=(a²+2ab+b²)(a+b)=a³+a²b+2a²b+2ab² + ab²+b³=

=a³+3a²b+3ab²+b³. 

(a-b)³=(а-b)²(a-b)=(a²-2ab+b²)(a-b)= a³-a²b-2a²b+2ab² + ab²-b³=

=a³-3a²b+3ab²-b³. 

Завдання для груп .

Піднести до куба: 1) (а+2)³; 2) (2в +1) ³;3) (1-х) ³; 4) (2в-1) ³  .

ХВИЛИНКА РЕЛАКСАЦІЇ.

(Учні заплющили очі і намагаються уявити райдугу. Відкривши очі , посміхаються один одному.)

Вчитель: Дощ пішов . Трава змочилась. В небі райдуга з’явилась.

Усміхається привітно-феєрична,семицвітна. Вибігайте люди з хати.

Її фотографувати. Нумо,швидше, не лінуйтесь. Чудо в небі, полюбуйтесь!

А дуга,мов коромисло. Над будинками нависла. Це дарунок Бога людям. Оком кинеш-тепло грудям.

ІV. Я-дослідник. Аналітичне дослідження з учнями всіх груп.

Пропоную уважно розглянути формулу (a+b)³=a³+3a²b+3ab²+b³.Що ви можете сказати за показники числа а? (спадають); числа b? (зростають).

А якщо піднесемо двочлен до четвертого степеня, які будуть показники степенів? (Розписати без коефіцієнтів:

(a+b)⁴=  a⁴+  a³b+   a²b²+   ab³+   b⁴.)

 Чого не вистачає в цій формулі? (Коефіцієнтів.) Спробуємо знайти їх.

Давайте запишемо степені суми двох чисел – нульову , першу, другу та третю:

 (a+b)⁰=1;

(a+b)¹=a+b;

(a+b)²=a²+2ab+b²;

(a+b)³=a³+3a²b+3ab²+b³

 Випишіть тільки коефіцієнти, причому розташуйте їх у вигляді трикутника:

 

    1

1. 1

1  2  1

   1  3  3  1

Можна побачити, що “сторони” цього трикутника складені із одиниць, а числам, які стоять всередині  трикутника, притаманна властивість. Яка? (Кожне число можна подати у вигляді суми чисел, які стоять над ним у попередньому ряду праворуч і ліворуч:

  3=1+2;  2=1+1.)

Спробуйте дописати наступні рядки і  виправити формулу четвертого степеня двочлена:

(a+b)⁴ =a⁴+4a³b+6a²b²+4ab³+b⁴.

 Трикутник, складений за вказаним правилом, називають трикутником Паскаля, ім’ям відомого математика, фізика, філософа, письменника Блеза Паскаля (1623 - 1662), сучасника Декарта і Ферма.

 Де ви чули це прізвище?Демонстрація слайду з портретом Б.Паскаля

•      На уроках фізики: тиск вимірюється в паскалях.
•      На уроках інформатики: існує мова програмування  Паскаль.

Це була дивовижна людина. 12-річним хлопчиком він доводить неймовірний факт: у будь-якому трикутнику сума всіх трьох кутів разом складає два прямі кути (зараз ми сказали б 180^о). У 16 років він здійснив справжнє наукове дослідження: відкрив нові властивості конічних перерізів. У 23 роки він завершив виснажливу роботу над першою в світі арифметичною машиною, за допомогою якої можна було виконувати дію додавання та віднімання. Саме завдяки цьому в інформатиці одна з мов програмування названа його іменем. А крім цього роботи з фізики, комбінаторики, філософські роздуми та багато іншого.

Vетап. Підсумок уроку . Оцінювання.Рефлексія.

От  і добіг кінця урок. А чи засяяла для вас райдуга? Чи цікаво вам було побувати в ролі дослідників? І неважливо ,що хтось із вас робив помилки. Помилку можна виправити. Треба тільки наполегливо працювати і не опускати руки. Головне,щоб ви не боялися труднощів, а вперто йшли до поставленої цілі. Гіпотезу Пуанкаре, яка була сформульована в 1904 році довів відомий математик Григорій Перельман у 2002-2003рр.

Консультанти підраховують кількість отриманих балів.

Отже, на уроці я …(метод «Мікрофон» )

1. Відпрацювали вміння підносити двочлен до куба.

2.Навчились виводити формулу квадрата многочлена.

3.Навчились підносити двочлен до будь-якого натурального степеня та ін... 

VІ етап.  Домашнє завдання.

§13,№453, піднести двочлен до п’ятого степеня (a+b)⁵

 

Список використанихджерел.

1. Алгебра.5-9клас: Навчальнапрограмазагальноосвітніхнавчальнихзакладів ( затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804)

2.Концепціяновоїукраїнськоїшколи: Нова українська школа: Концептуальні засади реформуваннясередньоїосвіти. URL:

 https://mon.gov.ua/ua/tag/nova-ukrainska-shkola

3. Алгебра: підручн. для 7-го кл. загальноосвіт.навч.закл./ О.С. Істер.- Київ: Генеза,2015.- 256 с.

4.  Корнієнко Т.Л.,Фіготіна В.І.Алгебра.7 клас: плани-конспекти на друкованій основі – Х.: Вид-во «Ранок», 2015.- 128 с.– (Серія «Конструктор уроку») .