Урок "Функції, многочлени, рівняння, нерівності".

Функції, многочлени, рівняння, нерівності.

Якщо запастися терпінням і проявити старання,

то посіяне насіння знання неодмінно дасть добрі сходи.

Леонардо да Вінчі

Мета: Розширити знання учнів з теми «Функції, многочлени, рівняння, нерівності», вчити застосовувати набуті знання, розвивати логічне мислення, практичні навички у нестандартних ситуаціях, формувати математичні компетентності.

Тип уроку: підсумковий урок,  урок-практикум.

Зміст уроку:

 «Не кажи — не вмію, а кажи — навчусь!»

Вступ. Сьогоднішній урок – підсумковий урок з теми  «Функції, многочлени, рівняння, нерівності». У кожного з вас є вже відома вам картка успіху (таблиця результатів), заповнюйте її протягом уроку а  я  поставлю загальну оцінку за урок.

І. Актуалізація опорних знань(«Незакінчене речення»)

Запитання до класу(за кожну відповідь – 1 бал)

1. Функція – це
2. Основні характеристики функції – …( ОВ, ОЗ, графік, зростання, спадання, парність
3. Рівняння – це…(рівність зі змінною)
4. Розв’язати систему рівнянь … (знайти всі спільні розв’язки двох або кількох рівнянь, або довести що їх не існує)
5. Якщо рівняння, крім змінної містить невідоме… (то його називають рівнянням з параметром)
6. Параметр це -  …(незалежна змінна, значення якої є фіксоване чи довільне дійсне число, або число, що належить заданій множині)
7. Розв’язати задачу з параметром – це знайти …(значення змінної для всіх значень параметра )
8. Способи розв’язування нерівностей - …(рівносильні перетворення, метод інтервалів)
9. Многочлени від однієї змінної називають рівними коли…(коли в них рівні коефіцієнти при відповідних степенях)
10.           Остача від ділення многочлена 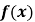на двочлен (x - a) = … значенню многочлена при х = а
11.           Будь-який цілий корінь многочлена з цілими коефіцієнтами … є дільником його вільного члена.

 

ІІ. Повторення та систематизація знань:

На дошці  ви бачите 2 задачі. Яким способом ви б розв’язували ? (2 учні до дошки)

(3б.)Знайдіть дійсні корені рівняння і розкладіть на множники:

 

використай ділення «кутом»

використай схему Горнера

 

 А ми разом попрацюємо усно. Увага на екран.

 

(1б.)При яких значеннях а, b, c, d  многочлени рівні?

 

a)  і       

б)і       

в) і       (інт. провокація)

 

Виконання вправ:

(1б.)1. При якому значенні а многочлен Р(х) ділиться без остачі на многочлен Q(x):

а)              (а=90)

б)               (а= -3)

 

(3б.)2. Не виконуючи ділення знайдіть остачу від ділення многочлена

      на квадратний тричлен    

Відповідь:

 

 (1б.)А зараз давайте повторимо графіки залежностей, які найчастіше зустрічаються

Коло   (x-a)² + (y-b)²=R²    центр?   радіус?

a – змінна b – const R - const	коло «рухається» вздовж осі Ох
b – змінна a  - const R - const	коло «рухається» вздовж осі Оу
a – const b – const R - змінна	«сім’я» концентричних кіл з центром в точці (а; b)

Півколо    у =

Графік залежності виду  |х| + |у|= т – квадрат

|х - а| + |y  -  b|= т

a – змінна b – const т - const	квадрат «рухається» вздовж осі Ох
b – змінна a  - const т - const	квадрат «рухається» вздовж осі Оу
a – const b – const т - змінна	«сім’я» концентричних квадратів з центром в точці (а; b)

 

 

 

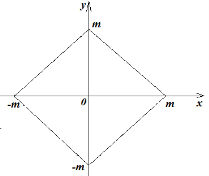
Графік функції виду  у = |х - а| + |х - b|

«дно»:  у = |а - b|

 

 

 

 

 

 

 

Усно:

(1б.)Яку найбільшу кількість розв’язків має рівняння в залежності від параметра а .(Розв’язуємо графічно)

1. 
2. 
3. 

 

 

4. 
5. 
6. 

 

«Із учителем - без учителя».

(1б.)З учителем (біля дошки):

Розв’яжіть рівняння:

1. 
2. 
3. 2

Розв’яжіть нерівності:

1. 
2. 

 

Без учителя (в парах):

(4б.)Знайдіть всі значення параметра а при якому рівняння має менше 4 коренів

 

Розв’язання.

Зліва виділимо повний квадрат і запишемо рівняння в виді: 

Нехай  f(x) =          g(x)=

Схематично зобразимо  графіки функцій f(x) та g(x)

Графік функції   g(x)=  - пряма, паралельна осі Ох. Розв’язки рівняння – абсциси точок перетину графіків функцій. Пряма не перетне графік f(x), якщо а < 0 і якщо а >9, то пряма матиме з графіком менше чотирьох точок перетину (а саме дві). Тобто, рівняння має менше 4 коренів коли

 

Відповідь:  

 

 

 (5б.)Розв’яжіть нерівність для всіх дійсних значень параметра а.

|x - 2|+|x + 3|≤ a

Розв’язання

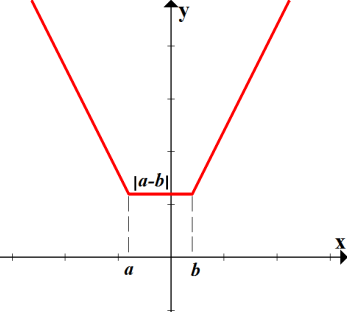
Побудуємо графіки функцій  у=|x - 2|+|x + 3| і  у=а

При a<5 графіки не перетинаються, і ніяка частина у=|x - 2|+|x + 3|  не лежить нижче прямої, тож нерівність розв’язків не має

При a=5 графіки мають спільний відрізок який і є розв’язком

При a >5 графіки  перетинаються в двох точках, частина графіка у=|x - 2|+|x + 3|   лежить нижче прямої у = а

 

 

 

 

 

 

 

 

 

 

 

 

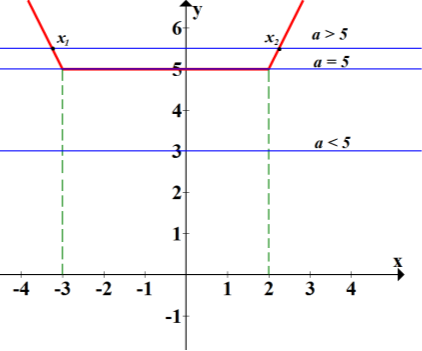
Знайдемо точки перетину у=|x - 2|+|x + 3| і у=а

При а>5 графіки перетинаються в точках х₁=     і     х₂=

 

 

Відповідь: якщо a<5                

якщо = 5,            

якщо

 

 

 

Попрацюємо разом

(4б.)Знайти всі значення параметра а при яких найменше значення функції  f(x) дорівнює найбільшому значенню функції     g(x).

 

f(x ) =  |x - 1|+|x - 3|+a

 

g(x) =

Розв’язання

Графік  функції  g(x)- парабола, вітки вниз, найбільшого значення досягає в вершині: х = 0;  g(x)=

f(x)=|x - 1|+|x - 3|+a

Побудуємо графік  у =|x - 1|+|x - 3|. 

Найменше значення f(x) = 2+a

Значить

Відповідь:  

 

 

 

 

Хвилинка відпочинку (портрети математиків)

4) (5б.) Знайдіть всі значення параметра при якому система має безліч розв’язків

Розв’язання

Побудуємо графіки обох рівнянь в одній системі координат.

Графік першого рівняння – дві паралельні прямі: y = x + 2 і  y = x – 2

Графік другого рівняння – кут, що рухається вгору-вниз по вісі Оу.

Кутові коефіцієнти прямих і правої сторони кута однакові і  дорівнюють 1.

 

 

 

 

 

 

 

 

 

Очевидно, що система має безліч розв’язків при а = ±2

Відповідь: -2; 2.

А тепер давайте знайдемо такі значення а при яких система має 1 розв’язок.

Очевидно, що система має один розв’язок  при  -2 < а < 2

 Відповідь:

 

Коло ідей(7б.)

5.  Знайдіть всі значення параметра при якому система має рівно два  розв’язки

 

Розв’язання

Побудуємо графіки обох рівнянь в одній системі координат.

Для побудови графіка першого рівняння розкриваємо модуль.

  Графік другого рівняння – квадрат, що рухається вздовж Ох.

Якщо а ≥ 1, то система завжди має 2 розв’язки.

Ще один випадок двох розв’язків матимемо, при а = -2

В інших випадках система не має розв’язків, або їх кількість не дорівнює двом.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

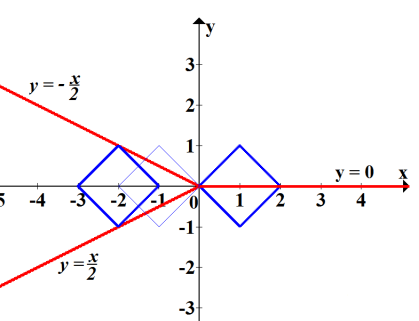
Відповідь:

 

Д/З   ст. 155 №10, 15, 16, 29

Картка успіху

П.І.	Бачити помилку	Проаналізувати умову	Запропонувати крок розв’язування	Аргумен-тувати	Запропонувати спосіб розв’язування	Відповісти на запитання	Відповідь біля дошки

 

Мої враження про урок

+ Плюс	Мінус	?!! Цікаво