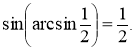Урок "Функція, обернена до y=sin x"

Розділ 1.   Функція, обернена до .

Введемо обернену функцію, використовуючи загальний алгоритм знаходження функції, оберненої до даної.

З властивості періодичності функції випливає, що кожне своє значення y вона приймає для нескінченої множини значень аргументу х=х₀+2πn. Це значить, що функція не є оборотною на всій області визначення. Разом з цим, на всіх проміжках де вона зростає чи спадає, для неї існує обернена. Оберемо такий з проміжків монотонності, в якому значення х  найближче до 0. цей проміжок .

Будемо вважати y незалежною змінною, а x – залежною, і розв’яжемо рівняння відносно x. Це значить, що треба знайти таке число x (кут або дуга), синус якого дорівнює y. На обраному проміжку таке число буде єдиним. Для його позначення використаємо символ . Отже, під знаком міститься значення синуса, а – функція, обернена до , якщо x.

Змінимо позначення залежної і незалежної змінної. Отримаємо функцію , обернену до , якщо x, записану в прийнятих позначеннях.

Графік функції отримаємо з графіка , якщо x, перетворенням симетрії відносно прямої .

Властивості функції .

1. Областю визначення функції 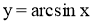є множина 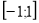; областю значень–множина .
2. Графік функції симетричний відносно початку координат, тобто 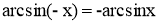– функція непарна.
3.   Функція не є періодичною.
4. Функція дорівнює 0 при х=0.
5. Зростає за теоремою про вл-ті оберненої функції.
6. Додатна при 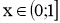, від’ємна при .
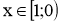7. Приймає найбільше значення, яке дорівнює 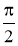, якщо х=1, і найменше 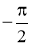, якщо х=-1.

8.  Якщо в рівності замінити y на , тому що , то                  

Якщо від рівності перейдемо до оберненої функції , а в останній рівності замінимо y на , то отримаємо ще одну рівність

Приклади: