Урок "Функція. Область визначення та значень"

Конспект уроку з алгебри для 9 класу

Тема уроку 2: «Властивості функції: нулі функції, проміжки знакосталості, проміжки зростання та спадання. Елементарне дослідження та побудова графіків функції.»

Мета уроку:

навчальна: формувати  знання учнів про зміст понять: нулі функції; проміжки знакосталості функції: функція, що спадає, зростає на проміжку. Сформувати вміння відтворювати означення вивчених понять.

розвивальна: формувати  уявлення про ідеї і методи графічного відображення залежних величин  та її роль у пізнанні навколишнього світу; розвивати  алгоритмічне мислення учнів, логічне мислення, просторову уяву, наочно-дійове мислення учнів;

виховна: виховувати: алгоритмічну культуру, звичку до системної розумової справи, вміння працювати в групі.

Форма проведення заняття: урок

Тип уроку: формування  знань та вмінь.

Обладнання: комп’ютер, презентація, підручники.

План уроку:

I. Організаційний етап.

Підготовка учнів до роботи на уроці. Створення позитивного настрою учнів.

ІІ. Актуалізація опорних знань, умінь, навичок.

Перевірка ДЗ та підготовка до вивчення нової теми

Опитування “ Закінчи речення ”

1. Функціональною залежністю  називають правило за яким..... (незалежній змінній ставиться у відповідність одне значення залежної змінної).
2. Область визначення  функції це множина ........ при яких.......
3. Множина змінної Y утворює область.......
4. Оберненою  пропорційністю називається функція виду.....
5. Графіком лінійної функції є ....
6. Знайти значення функції F(x) в точці x₀ значить підставити........ та обчислити...
7. Змінну х називають .......(незалежною або аргументом), змінну y називають (залежною або функцією)

Робимо разом:  №№ 7.14, 7.15 [1]

ІІ. Формування мети й завдань уроку.

Вчитель: ви дали правильні відповіді на питання, але, встеж – таки, чому виникле  поняття функціональної залежності та які вчені стояли у джерел даного поняття? Про це  ви могли прочитати у своєму підручнику. І зараз перевіримо як ви уважно читаєте параграф.   (слайд 2, діти читають характеристику вчених та за портретом вказують його прізвище).

III. Мотивація навчальної діяльності

Вчитель: Як ми бачимо, великі уми попередніх віків досліджували функції і наша задача  з вами навчитися користуватися надбанням предків у своїй діяльності, оскільки, як ми вже знаємо, функція та її графік використувуються в широкому спектрі життя (наукових дослідження, медицині (кардіограма) , економіці,  прогназуванні)

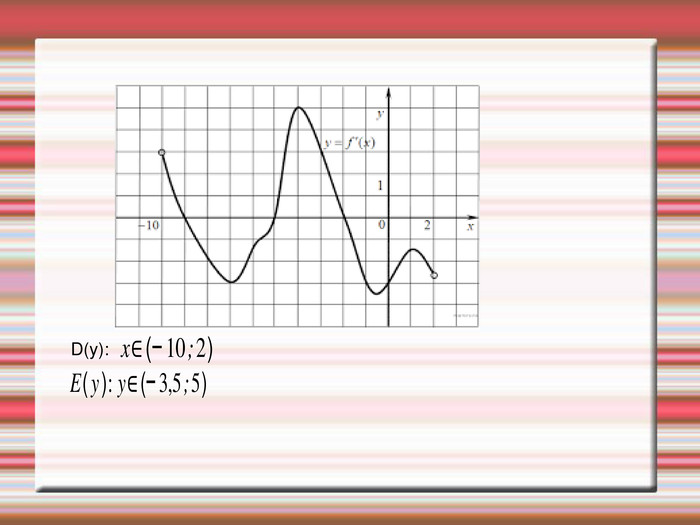
Розглянемо графік функції (слайд 3). За цим графіком ми з вами вже можемо визначити, що областю визначення є D(y):, а областю значень є 

Сьогодні ми ознайомимося з іншими властивостями функції,  а саме: нулі функції, проміжки знакосталості, проміжки зростання та спадання. Навчимося практично застосовувати вміння визначати властивості функції для побудови її графіка, бо  сприйняття картинки полегшує розуміння того з чим ми маємо справу  та для яких цілей. 

ІV. Вивчення нового матеріалу: теорія, практика.

Вчитель:   Розглянемо графік функції на наступному слайді.

Якого значення набуває функція коли х={-9, -5, -2} Правильно, нуль.

Означення 1: Значення аргументу Х при яких функція Y  дорівнює нулю називається нулем функції.

Виконуємо разом: №№ 8.7 стор 74

 Повертаємося до нашого графіка функції. З малюнка ми бачимо, що деяка частина графіка знаходиться вище вісі ОХ, тобто всі значення змінної Y є додатними  числами, а деяка чистина розташована нижче вісі ОХ, тобто зміна Y<0.  Визначимо за малюнком ці проміжки :

.

Такі проміжки називаються проміжками знакосталості.

 Означення 2: Кожний з проміжків, на якому функція приймає значення одного знаку називають проміжком знакосталості функції.

Виконуємо разом: №№ 7.3 стор 83

При вивчення графіка функції ми також можемо помітили, що існують  інтервали на яких графік як би “падає вниз”, тобто значення змінної Y зменшується при  русі вправо по вісі ОХ, а  також, існують інтервали де функція “підіймається вверх”, тобто значення змінної Y  збільшуються при русі вправо по вісі ОХ.

  Такі проміжки називаються проміжками спадання та зростання.  Розглянемо наш графік . Проміжками спадання та зростання є

.

Означення 3: Функція f називають зростаючою на деякому проміжку, якщо для будь-яких значень аргументу з області визначення функції,  таких що x₁>x₂  виконується нерівність f(x₁)>f(x₂).

Означення 4: Функція f називають спадаючою або спадною на деякому проміжку, якщо для будь-яких значень аргументу з області визначення функції,  таких що x₁>x₂  виконується нерівність f(x₁)<f(x₂).

Виконуємо разом: №№8.9,  8.15;  8.21

V. Етап перевірки первинного розуміння, закріплення і корекція

Завдання групам:

Група 1 за виглядом  графіка функції охарактеризувати її: № 8.5 стор 73

Група 2 за характеристикою  функції побудувати її графік: № 8.11 стор 74

VI. Підведення підсумків уроку

Метод: опитування .

 - Що нового ви дізналися на уроці?

 - З розумінням якої властивості у вас виникли труднощі?

IX. Повідомлення домашнього завдання  та оцінок за урок

§ 8 стор. 68  опрацювати, вивчити означення властивостей функції.

 Використана література:

1. Мерзляк А.Г., Полонський В.Б., Якир М.С. АЛГЕБРА, Харьків “Гімназія”, 2017.
2. Богатырев Г.И., Боковиев  О.А. Математика для подготовительных курсов техникумов, 1988

Слайди презентації до уроку