Урок "Квадратична функція"

Конспект уроку з алгебри для 9 класа

Тема уроку 5:   «Квадратична функція. Її властивості та графік.»

Мета уроку:

навчальна: формувати вміння розпізнавати квадратичну функцію серед інших елементарних функцій та будувати її графік;

розвивальна: формувати  уявлення про ідеї і методи представлення залежних величин; розвивати  вміння слухати, уміння  аналізувати, класифікувати; алгоритмічне мислення учнів, логічне мислення, просторову уяву;

виховна: виховувати: інтерес до вивчення математики, фізики, потяг до наукової творчості.

Форма проведення заняття: урок-діалог

Тип уроку: урок формування нових знань та вмінь

План уроку:

I. Організаційний етап.

 Привітання з учнями  та ство­рення психологічної атмосфери уроку й організаційних умов, за яких досягається успіх навчальної діяльності.

Перевірити домашнє завдання. Розібрати питання, що виникли при  виконанні домашнього завдання.

II. Мотивація навчальної діяльності та актуалізація опорних знань, умінь, навичок.

Вчитель:

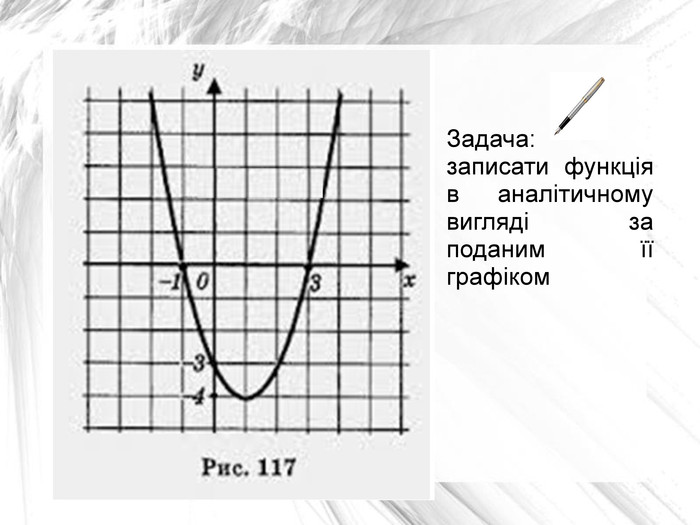
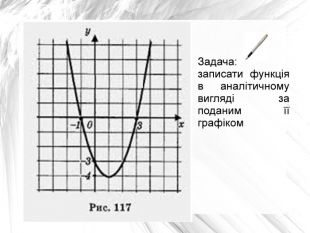
 Задача: записати аналітичний вид функції графік якої ви бачити на малюнку (слайд 2).

 (Застосовуючи знання графічного перетворення графіків функцій, приходимо до висновку, що даний графік отриманий від графіка функції y=x²  шляхом паралельного переміщення по вісі OX на одиницю вправо  і на чотири одиниці вниз по вісі OY. Таким чином, аналітичний вид нашої функції має вид якщо ми розкриємо дужки та  зведемо подібні доданки то отримає наступний               вигляд:

В результаті ми отримали  квадратний трьохчлен,  і на практиці впевнились що графіком такої функції є парабола.)

III. Формування мети й завдань уроку.

Отже сьогодні на уроці ми ознайомимось з означенням квадратичної функції, її графіком та властивостями.

IV. Вивчення нового матеріалу: теорія, практика.

Означення: Функція, яку можна задати формулою ,  де х — незалежна змінна, a, b, c — деякі числа, причому , називається квадратичною.

Квадратична функція не є для вас новою, по-перше, у 8 класі ви ознайомились з функцією  y=x^2. . На уроці геометрії ви розглядали задачі на обчислення площі кола.  Формула  S(r)=π*r^{2  -} є квадратичною функцією дe S — залежна змінна, r - незалежна змінна.

На уроках фізики ви знайомились з формулою  знаходження висоти тіла, що було підкинуто вверх зі швидкістю  v₀ в певний момент часу t

.

З нашого графіка ми також можемо зробити висновок що квадратична функція має два способа аналітичного запису,  а саме  .

Як отримати другий запис квадратичної функції  розглянете самостійно.

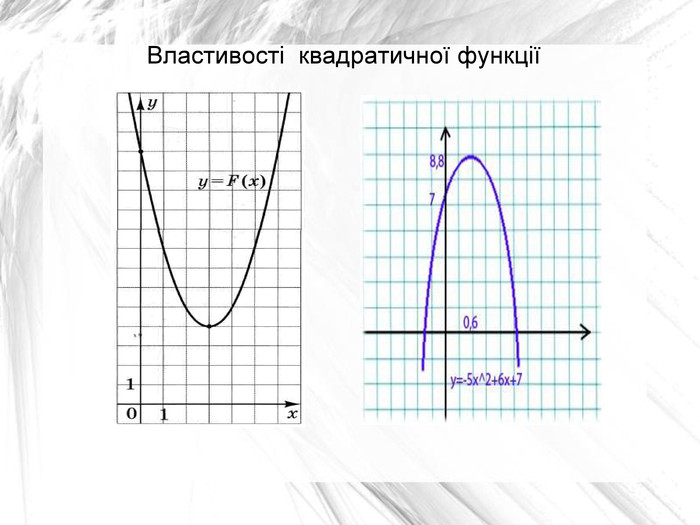
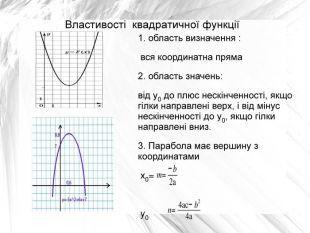
З’ясуємо властивості квадратичної функції :

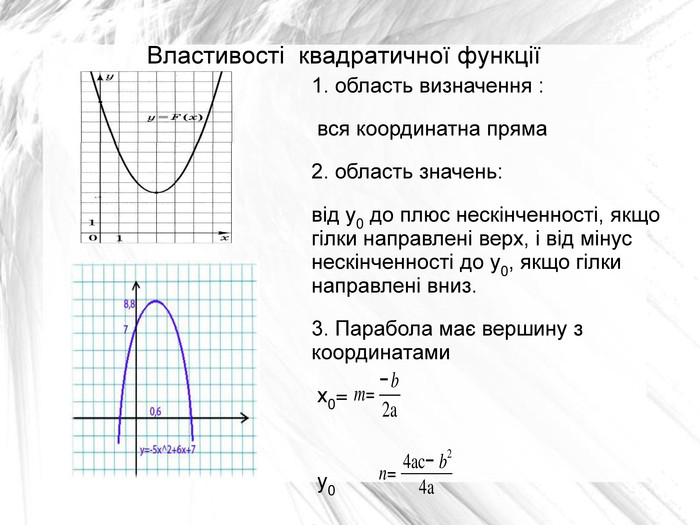
• область визначення : вся  координатна пряма
• область значень: від  y₀  до  плюс нескінченності, якщо гілки направлені верх, і від мінус нескінченності до  y₀, якщо гілки направлені вниз.
• Парабола має вершину з координатами х₀=, y₀=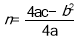

Розглянемо алгоритм побудови  квадратичної  функції

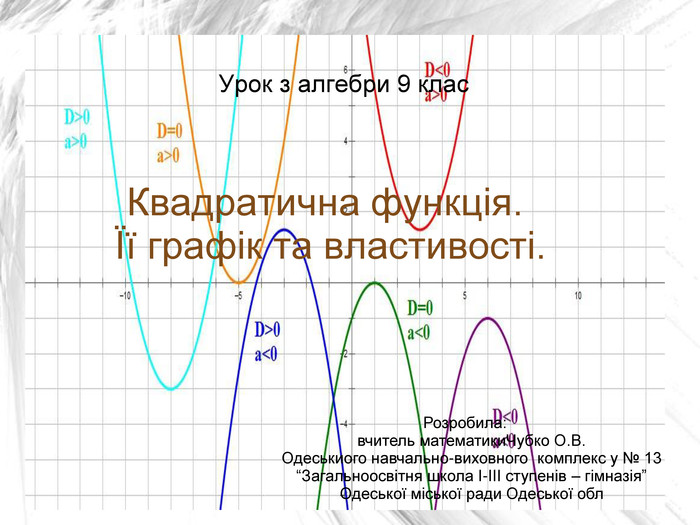
1. Визначаємо направлення гілок; залежить від знаку числа а. (слайд 3);
2. Обчислюємо координати вершини: знаходимо за формулами

х₀=, y₀= та відмічаємо точку вершини на координатний прямій;

3. Знаходимо ще декілька точок параболи (точки перетину з осями координат) і також відмічаємо їх на координатній прямій;
4. Через отримані точки проводимо криву параболи.

VI. Первинне закріплення і корекція

Стор. 101-102:  №11.1( які функції є квадратичними);  №11.5 (визначити напрямок гілок та координати вершини)

VII. Етап перевірки первинного розуміння

Стор. 102: №11.6(3, 5, 6) (Побудувати графік функції); 

№11.12 (розв’язати графічно рівняння);  №11.18 (Знайти область значень, та проміжки зростання та спадання); №11.20 (Побудувати графік та вказати властивості функції)

VIII. Підведення підсумків уроку

Опитування:

1. Що називаємо квадратичною функцією?
2. Від чого залежить направлення гілок параболи?
3. Як знаходяться точки перетину графіка параболи з осями координат?
4. Які формули для знаходження координат вершини параболи?

IX. Повідомлення домашнього завдання

§11 опрацювати, №№ 11.9; 11.21, 11.54(повторення)

Використана література:

1. Мерзляк А.Г., Полонський В.Б., Якир М.С. АЛГЕБРА, Харьків “Гімназія”, 2017.
2. Богатырев Г.И., Боковиев  О.А. Математика для подготовительных курсов техникумов, 1988
3. Титаренко А.М. Форсированный курс школьной математики, Харьков, 1996