Урок "Функція y = k / x, графік та властивості"

Функція , її графік та властивості

Дидактична мета: формувати уявлення учнів про обернену пропорційність як функцію, сформувати первинні вміння; виділяти серед запропонованих функцій обернено пропорційні, відтворювати властивості обернено пропорційних функцій, будувати графіки функцій, які є обернено пропорційністю із заданим коефіцієнтом.

Розвивальна мета: розвивати логічне мислення та інформаційні компетенції; вміння систематизувати та робити узагальнення.

Виховна мета: виховувати інтерес до математики; сприяти розвитку в учнів пізнавальних здібностей.

Обладнання: комп’ютери, роздатковий матеріал, підручник «Алгебра» А. Г. Мерзляк.

Хід уроку

І. Актуалізація опорних знань

Учитель: в природі, в житті багато реальних процесів і явищ ідуть поруч, існують парами. Так, наприклад, заряди є позитивні і негативні, люди активні і пасивні, є день і ніч, є молодість і старість, є дія додавання і віднімання, множення і ділення; є залежність між величинами прямо пропорційна та обернено пропорційна .

На цьому уроці ми розглянемо обернену пропорційність як функцію, побудуємо її графік та дослідимо властивості. То що ми повинні згадати, щоб все це зробити?(відповіді учнів)

Визначимо вид залежності:

1) довжина сторони квадрати і його периметр (пряма);

2) довжина та ширина прямокутника заданої площі (обернена);

3) витрачений час і обсяг виконаної роботи (пряма);

4) швидкість і час руху автомобіля для заданої відстані (обернена);

5) обсяг і якість виконаного домашнього завдання та отримана оцінка (пряма);

6) оцінка в щоденнику та радість батьків (пряма).

То щоб радість була якнайбільшою, оцінка хорошою чи відмінною, включаємося в роботу, обговорюємо, помиляємося і досягаємо мети.

Щоб згадати основні поняття, пов’язані з функцією, виконаємо завдання «Вставити пропущені слова» (завдання на картці):

1. Відповідність між змінними х та у, за якої кожному значенню змінної х відповідає єдине значення змінної у – це функція.

2. Змінна х – аргумент.

3. Змінна у – функція.

4. Усі значення, яких набуває аргумент, утворюють область визначення функції.

5. Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють область значень функції.

6. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати – відповідним значенням функції, називають графіком функції.

ІІ. Сприйняття та усвідомлення нового матеріалу.

1) Для прямокутника  площею S = 24 см², виразити довжину у через ширину х.

  – це і є приклад функції оберненої пропорційності.

2) Робота за готовою таблицею, заповненою учнями вдома для функцій і . Учні будують графіки.

 

 

 

х	-8	-6	-4	-2	-1	-1/2	1/2	1	2	4	6	8
у	-1		-2	-1	-8	-16	16	8	4	2		1
х	-8	-6	-4	-2	-1	-1/2	1/2	1	2	4	6	8
у	1		2	1	8	16	-16	-8	-4	-2	-	-1

 

Учитель Ми побудували красивий графік – назва якого – гіпербола (в перекладі «кинути далі за ціль»); відкритий древньогрецькими математиками, а назву гіперболи графіку дав Аполлоній.

3) Робота з бібліотекою комп’ютерних моделей (https://sites.google.com/site/biblkompmod/).Учні, працюючи з моделлю, рухають повзунок та встановлюють розміщення гіперболи по четвертях і належність точки графіку функції.

4) Доповнення порівняльної таблиці властивостей функцій прямої та оберненої пропорційності.

ІІІ. Формування умінь і навичок

№ 319 – усно (с. 74):

Оберненою пропорційністю є:

3) , k = 2; 4) ; 5) ; 7) ; 8) .

№ 322:

- за побудованим раніше графіком

1) якщо х = 4, то у = -2,

   х = -1, то у = 8.

2) якщо у = 2, то х = -4,

  у = -8, то х = 1.

3) у > 0, якщо х < 0.

№ 324 (1, 2):

         

1) Якщо точка А(-4; 7) належить графіку , то виконується умова ; графік проходить через точку А(4; 7).

2) В(14; -2); , графік не проходить через точу В(14; -2).

№ 328:

Графік проходить через точку А(-5; 4), тому ; k = -20.

№ 331 (1): Розв’язати графічно

         

Будуємо графіки функцій (гіпербола) і у = 4 – х (пряма).

Графіки перетинаються в точці з абсцисою х = 2.

 

 

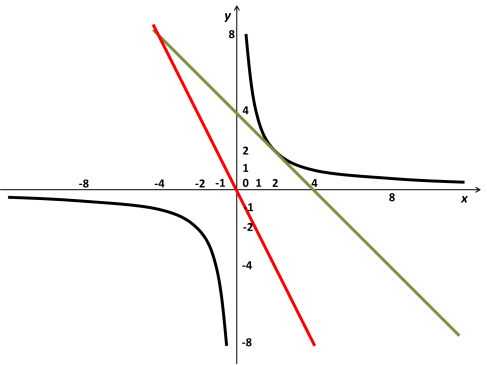
 А якщо необхідно розв’язати рівняння  ? (В цій же системі координат іншим кольором  побудуємо пряму у = –2 х  і робимо висновок,що гіпербола і пряма не перетинаються, а значить рівняння не має розв’язків).

   ІV. Підведення підсумків

Хто впевнений в собі, і хто хоче перевірити, як він засвоїв дану тему, можете пройти тест-контроль на комп’ютері і автоматичне оцінювання. А решта учнів зможуть пройти даний тест вдома.

1) Хочу почути запитання від вас щодо функції   , графік якої зображено на дошці (математичний футбол).

2) Які реальні процеси можна описати за  допомогою функції ?

V. Домашнє завдання

Опрацювати п. 10, № 323, № 329 (1), № 332 (1, 3).

 

 

 

 

 

 

 

 

 

 

 

Додатки

 

Встав пропущені слова

1.Відповідність між змінними    та    , за якої кожному значенню змінної 

            відповідає єдине значення змінної       — це...

2.Змінна х    — ...

3. Змінна у  — ...

4. Усі значення, яких набуває аргумент, утворюють область...

5. Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють область...

6. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається...

 

Встав пропущені слова

1.Відповідність між змінними    та    , за якої кожному значенню змінної 

            відповідає єдине значення змінної       — це...

2.Змінна х    — ...

3. Змінна у  — ...

4. Усі значення, яких набуває аргумент, утворюють область...

5. Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють область...

6. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається...

 

Встав пропущені слова

1.Відповідність між змінними    та    , за якої кожному значенню змінної 

            відповідає єдине значення змінної       — це...

2.Змінна х    — ...

3. Змінна у  — ...

4. Усі значення, яких набуває аргумент, утворюють область...

5. Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють область...

6. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається...

 

Встав пропущені слова

1.Відповідність між змінними    та    , за якої кожному значенню змінної 

            відповідає єдине значення змінної       — це...

2.Змінна х    — ...

3. Змінна у  — ...

4. Усі значення, яких набуває аргумент, утворюють область...

5. Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють область...

6. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається...

 

 

Тест

1. У яких чвертях розміщено графік функції у = 3 / 8х?

А. I і IV.                   Б. I і III.                   В. I і II.                     Г. II і IV.

2. У яких чвертях розміщено графік функції у = -1/2х

А. I і III.                    Б. I і IV.                  В. II і III.                   Г.  II і IV.

3. Задайте формулою обернену пропорційність, якщо її графік проходить через точку                    А(4;-0,15)

А. y = -0,375 / x.       Б. y = 0,375 / x.     В. y = 0,6 / x.              Г. y = -0,6 / x.

4. Яка з точок належить графіку функції у=-4/х ?

А. (1; 10).                  Б. (1; 4) .               В. (1; -4).                    Г.  (1; -10).

5. Знайти значення аргументу для функції у=6/х, якщо у=-3

А. 2.                           Б. 3.                       В. -3.                           Г. -2.

6. Яка з заданих функцій є оберненою пропорційністю?

А. y = 3x.                   Б. y = 3 / x             В. y = x / 3                 Г. y = -3 / x

7. Знайти значення функції у=6/х,якщо х=1,5

А. 0,4.                        Б. 4                        В. 5                             Г. 0,5