Урок-семінар "Властивості Функції"

Урок – семінар «Функція  , її графік та властивості»

Підготовчий етап

Клас попереджений про проведення семінару, поділений на групи: доповідачі, співдоповідачі. Доповідачі готують презентації по плану, співдоповідачі - приклади по кожному пункту плану. План проведення семінару повідомлений після теми: «Рівняння х²=а». Матеріали учні заздалегідь подають на перевірку, консультуються про форму проведення доповіді.

План проведення семінару

1.      Функція. Поняття незалежної та залежної змінних функції. Способи задання функції. Область визначення , область значень функції .
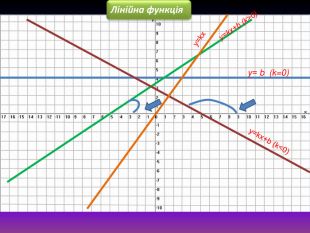
2.      Лінійна функція. Графік лінійної функції.
3.      Функція 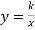,  її графік та властивості.
4.      Функція  у = х², її графік та властивості.
5.      Графічний спосіб розв’язування рівнянь.
6.      Функція 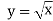  , її графік та властивості.

Мета: домогтися засвоєння учнями змісту основних властивостей функції , сформулювати вміння відтворювати вивчені властивості, а також використовувати їх у розв’язанні програмових задач.

Тип уроку: урок-семінар з вивченням нового теоретичного матеріалу

Наочність та обладнання: мультимедійне обладнання, презентації

Хід уроку

І. Організаційний момент

Учитель Вітаю всіх присутніх на уроці. Бажаю вам всім плідно попрацювати. Тиждень тому ваш клас був попереджений про проведення уроку – семінару.  Клас поділений на групи: доповідачі, співдоповідачі та опоненти. Матеріали, що готувалися на доповідь, заздалегідь були подані на перевірку, відредаговані і сьогодні ви маєте змогу познайомитися з ними. Доповідачем по останньому пункту буду я. Мета нашого уроку: систематизувати знання про функцію, графік функції, властивості функції, графічний спосіб розв’язування рівнянь; на основі набутих знань навчитися будувати графік функції та вивчити властивості цієї функції.

ІІ. Виступи учнів по плану

1. Виступ  доповідача. Демонстрація презентації «Функція».

Поняття «функція» пройшло довгий шлях свого розвитку. В роботі французького вченого П'єра Ферма «Ведення у вивчення плоских і тілесних місць» в 1676 р. зазначається: «Всякий раз, коли в підсумковому рівнянні є дві невідомі величини, то очевидним є місце». Тобто мова йде про функціональну залежність і її графічне зображення («місце» означає лінія). Вивченню ліній за їх рівняннями та взаємній залежності між двома змінними величинами приділяється увага і французьким вченим Рене Декартом у книзі «Геометрія». Поняття «функція» вперше ввів у 1694 році німецький учений Готфрід Лейбніц. Функцією він називав різні відрізки, що зв’язані з деякою кривою.

Більш наближене до сучасного означення функції трапляється в працях швейцарського вченого Йоганна Бернуллі (1713 р.), російського вченого Леонарда Ейлера (1748р.), французького вченого Жана Фур'є (1822р.), російського вченого Миколи Лобачевского (1834р.), німецького вченого Петера Густава Лежена (Діріхле)(1838р.), де вже вводяться позначення функції  f(x) і визначається функція аналітичним способом. У принципі, сучасне означення функції приписують німецькому вченому Діріхле.

Змінну у називають функцією від змінної  х, якщо кожному значенню змінної  х відповідає одне певне значення змінної у. При цьому змінну х, називають незалежною змінною, або аргументом, а змінну у – залежною змінною, або функцією (від аргументу х). Множину значень, яких набуває незалежна змінна (аргумент), називають областю визначення функції; множину значень яких набуває залежна змінна (функція), називають областю значень функції.
           Ми знаємо такі способи задання функції: аналітичний, графічний, табличний.

Виступ  співдоповідача. Прикладом функціональної залежності   є залежність значення периметра прямокутника від довжини прямокутника при сталій ширині, наприклад при ширині 5 см. Цю залежність можна записати формулою P=2(5+a), де  а - незалежна змінна, а Р – залежна змінна. Область визначення і область значень цієї функції є множина дійсних додатних чисел.

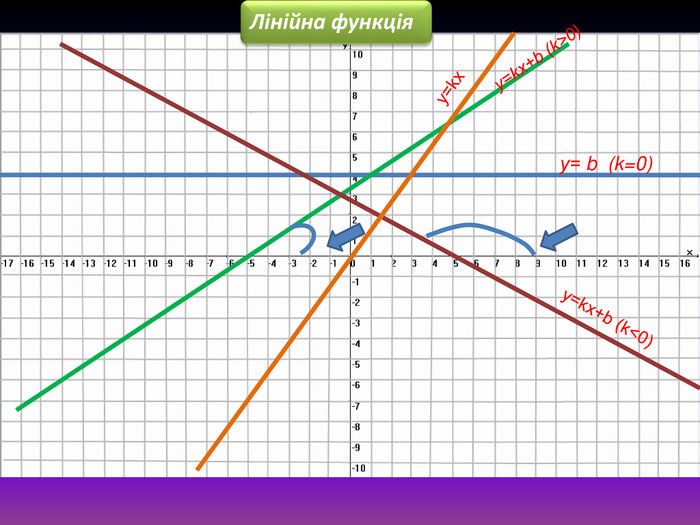
2.      Виступ доповідача. (Демонстрація презентації «Лінійна функція»).  Функція  виду  y = kx+b , де   k, b - деякі числа, називається лінійною. Область визначення і область значень є множина дійсних чисел. Графіком лінійної функції є пряма. Якщо k>0, то пряма розміщена під гострим кутом до осі абсцис. Якщо k<0, то пряма і вісь абсцис утворюють тупий кут. Якщо k=0, то пряма паралельна вісі Ох і областю визначення цієї функції є число  b. Якщо b=0, графік проходить через початок координат.

Виступ  співдоповідача.  Прикладом такої функціональної залежності є залежність об’єму води в басейні від часу при умові, що кожен час через трубу вливається 2,5  води і в басейні спочатку є вже 70 води. Цю залежність запишемо за допомогою такої формули: V= 2,5t+70.  В даному випадку незалежною змінною є час, а залежною змінною об’єм води.
            Побудуємо графік лінійної функції у=2х+3. Це пряма, яка проходить через точки (0;3) і (-1; 1). Область визначення даної функції є множина дійсних чисел, область значень – теж множина дійсних чисел.

3.      Виступ  доповідача. Оберненою пропорційністю називається функція, яку можна задати формулою вид 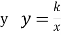, де х – незалежна змінна і k –число, що не дорівнює нулю. Областю визначення цієї функції є множина всіх дійсних чисел, відмінних від нуля. Це випливає з того, що вираз    не має зміст при х=0. Таким чином область визначення D(y): x ≠ 0. Оскільки k ≠ 0 , то й значення дробу   не може дорівнювати нулю. Звідси область значень функції   E(y): y ≠ 0. Криву, яка є графіком оберненої пропорційності, називають гіперболою. Гіпербола складається з двох гілок.

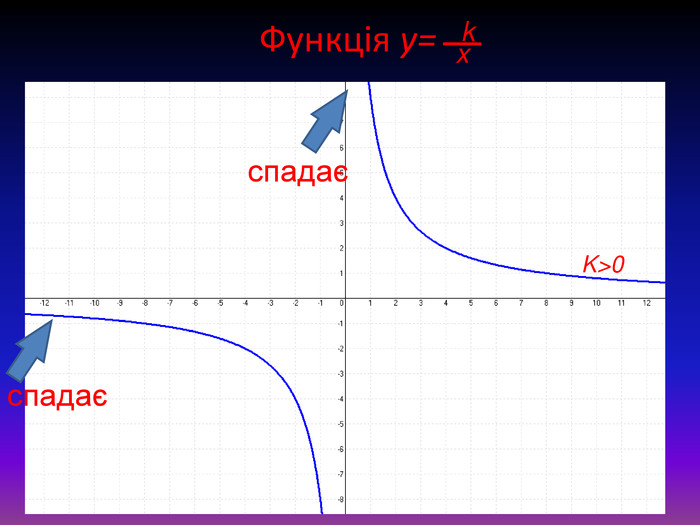
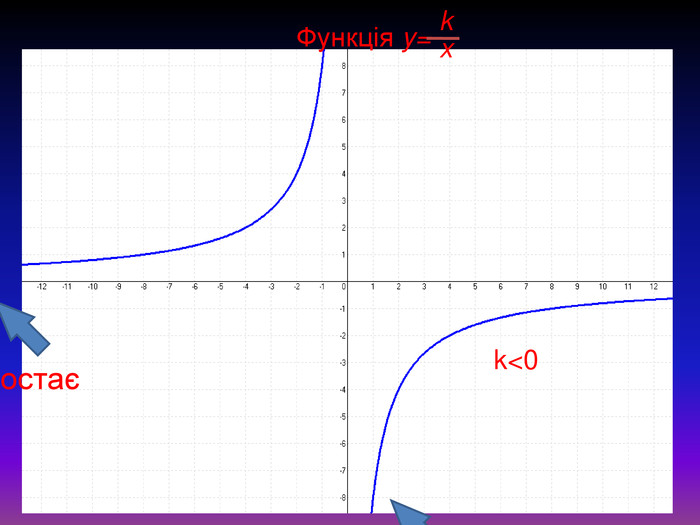
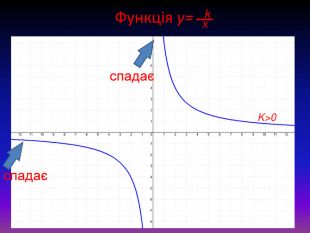
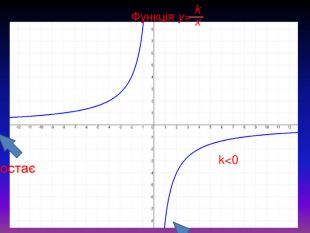
Якщо k>0, то графік розміщений в І і ІІІ координатних чвертях. При цьому функція спадає на всій області визначення. Якщо k<0, то графік розміщений в ІІ і ІV координатних чвертях. При цьому функція  зростає на всій області визначення. Кожна гілка гіперболи в одному напрямі наближається все ближче і ближче до осі Ох, а в іншому напрямі до осі  Оу. У подібних випадках відповідні прямі називають  асимптотами. Таким чином, гіпербола має дві асимптоти: Ох і Оу.

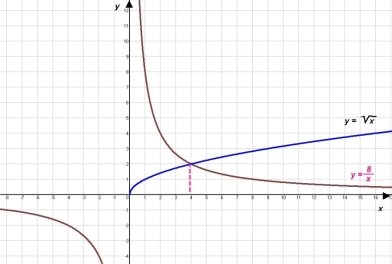
Виступ  співдоповідача. Досить часто трапляються ситуації, практичне розв’язання яких зводиться до встановлення залежності виду , де k ≠ 0 і x ≠ 0. Нехай групу учнів нашої школи – 165 школярів - треба повезти на екскурсію в Київ. Для цього треба замовити m автобусів по n місць у кожному. Очевидно, що кількість автобусів залежить від кількості посадочних місць. Цю залежність можна виразити аналітично: .  Зрозуміло, що область визначення  і область значень даної функції є множина натуральних чисел.

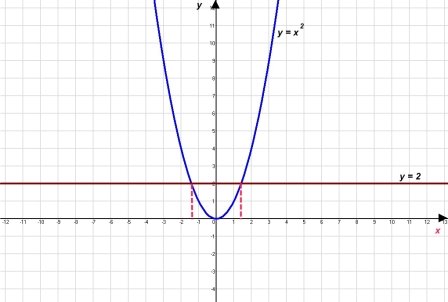
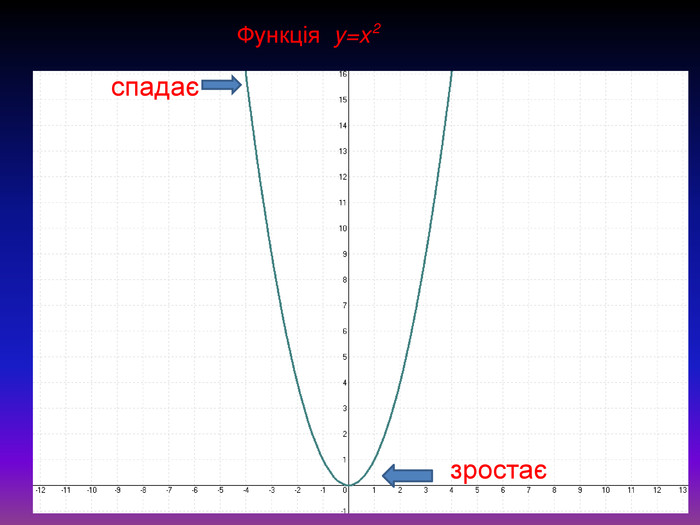
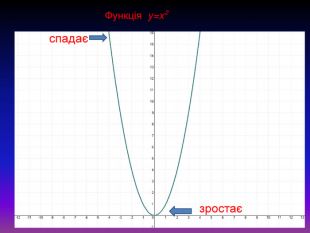
4.                Виступ  доповідача. Графіком функції у = х² є парабола. Вона має дві нескінчені гілки, які плавно сходяться в одній точці з координатами (0;0). Ця точка є вершиною параболи. За побудованим графіком легко визначити властивості функції. При будь-яких значеннях  х значення у буде невід'ємне. Отже  область визначення D(y) є множина всіх дійсних чисел, або х € R, область значень функції   E(y): y≥0, тобто множина дійсних невід'ємних чисел. При від'ємному значенні х значення функції зменшується, а при додатному аргументу значення функції зростає.

Виступ  співдоповідача. (  Перегляд презентації ). Розглянемо практичне завдання, в якому треба знайти площу квадрата, якщо відомо довжина його сторони. Очевидно, що кожному значенню сторони квадрата відповідає єдине значення його площі. Таку залежність площі квадрата від його сторони можна виразити за допомогою формули: S=a² (a≥0). Це, фактично, функціональна залежність між змінними S i a, де a – незалежна змінна, а S – залежна змінна.

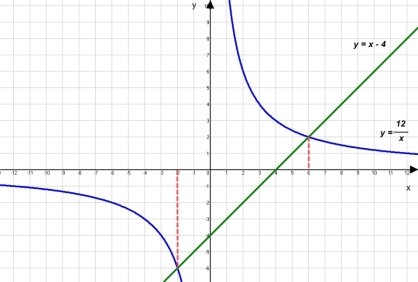
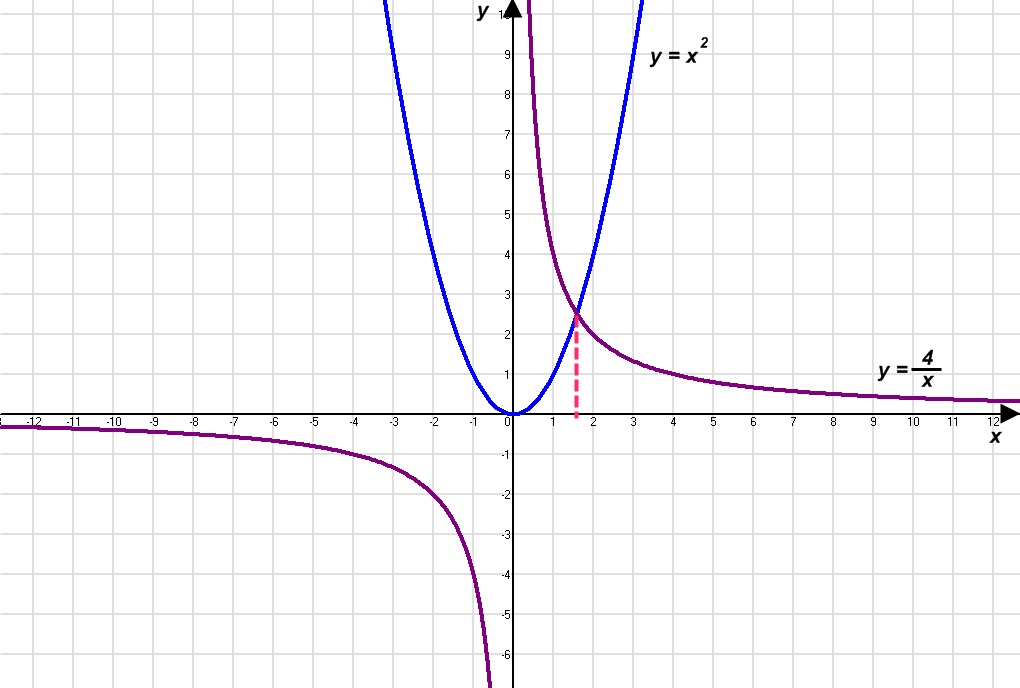
5.           Виступ  доповідача.  Вивчаючи  в 7 класі способи розв’язування систем лінійних рівнянь з двома змінними, ми розглядали графічний спосіб, тобто знаходили спільну точку перетину двох прямих. Графічний спосіб розв’язування рівнянь полягає в визначені спільних точок графіків функцій. Зручність цього способу полягає в тому, що графічна інтерпретація надає можливість одразу зробити висновок про кількість розв’язків. При розв’язуванні раціональних рівнянь аналітичним способом, ми зводимо їх до найпростіших за допомогою рівносильних перетворень. Проте окремі рівняння виду 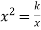, які зводяться до рівнянь виду 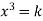ми ще не вміємо розв’язувати, тому в нагоді стає графічний спосіб розв’язування рівнянь. Таким чином, рівняння f(x) = g(x) можна розв’язувати графічним способом. Для цього:
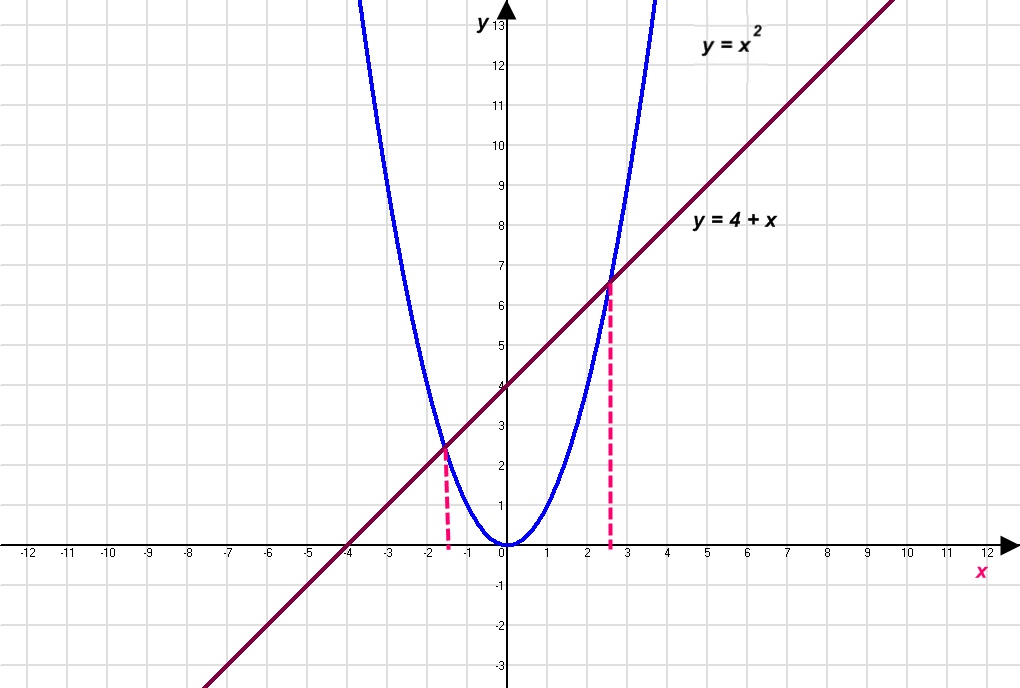
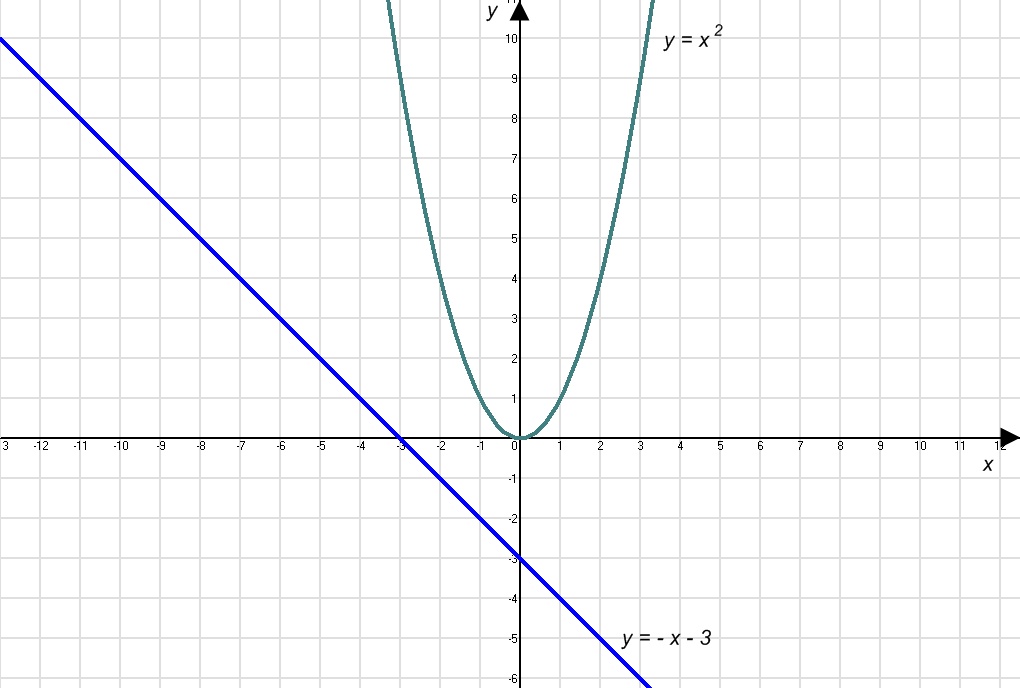
   1. Вводять дві функції: y = f(x) – функція, що визначається лівою частиною рівняння, і y = g(x) – функція , що визначається правою частиною рівняння.
   2. Будують графіки функцій y = f(x) і y = g(x) в одній системі координат і встановлюють координати їхніх спільних точок.
   3. Визначають абсциси точок перетину графіків, які є розв'язками рівняння f(x)=g(x).

Виступ  співдоповідача.

Розв’яжемо рівняння

,

.

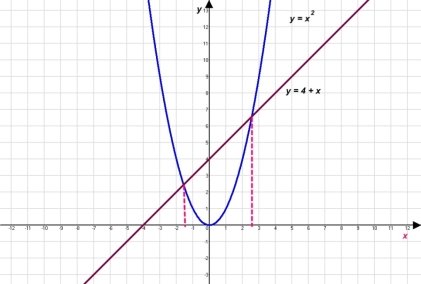
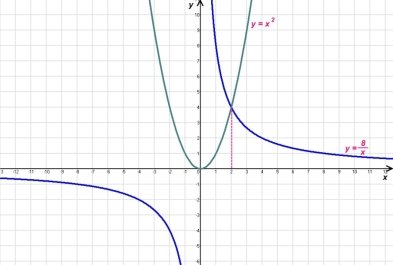
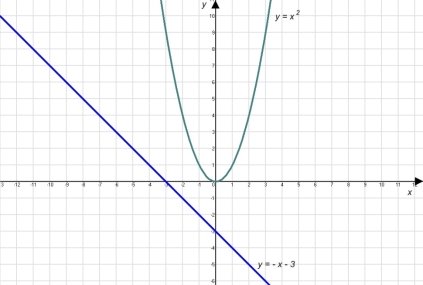
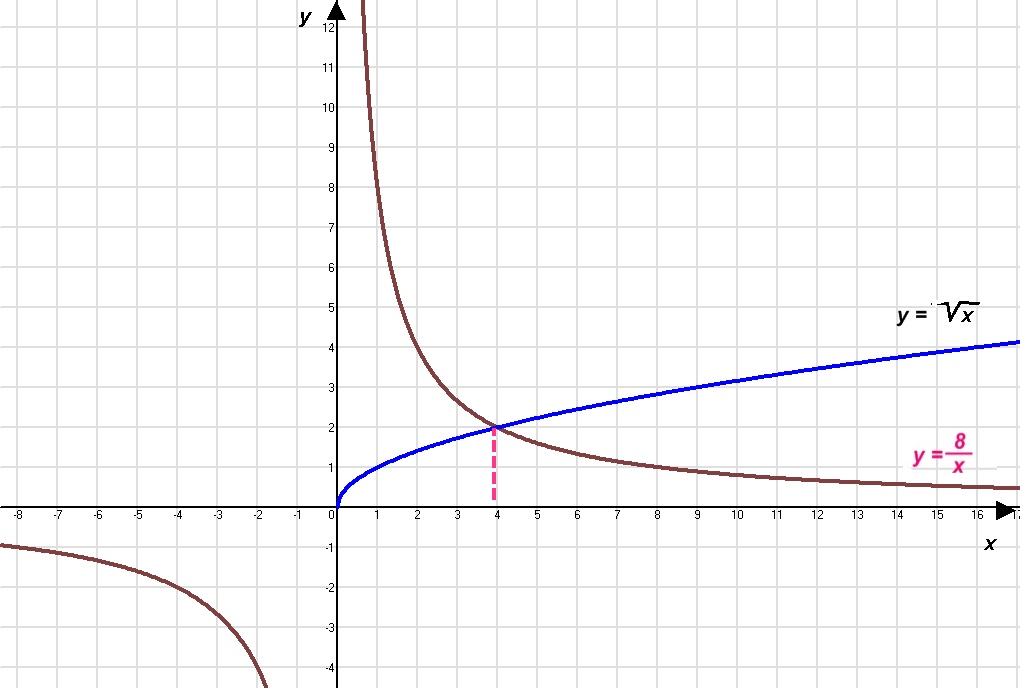
Учитель Розв’яжіть графічно такі рівняння:

Оцінювання зробленого завдання

ІІІ. Вивчення нової теми

Учитель Майже два роки ми вивчали властивості функцій і вже мабуть у вас склався певний алгоритм вивчення нової функції. З чого нам потрібно почати?

Учні Скласти таблицю значень.

Учитель Нагадаємо означення арифметичного квадратного кореня.

Учень Арифметичним квадратним коренем з невід’ємного числа а називається таке невід’ємне число х, квадрат якого дорівнює а.

Учитель Визначте, при якому значенні аргументу існує ця функція.

Учні Оскільки за означенням корінь квадратний добувається з невід’ємного числа, то аргумент набуває невід'ємних  значень.

Учитель Яких значень набуває  функція?

Учні За означенням теж невід'ємних.

Учитель Тобто яку частину площини нам слід взяти до уваги?

Учні Це перша координатна чверть, де і значення аргументу і значення функції невід'ємні.

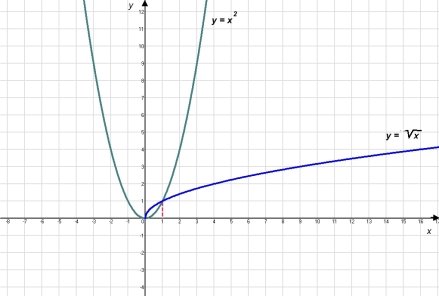
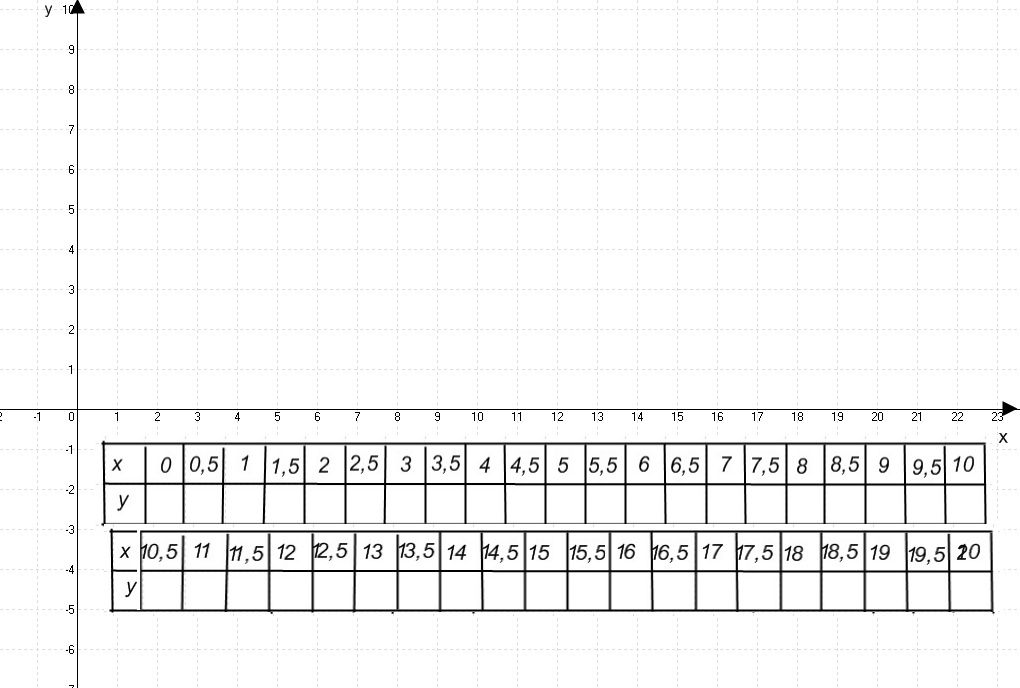
Учитель За допомогою калькуляторів складаємо таблицю значень від 0 до 10 з кроком 0,5, заповнюємо її, не забуваємо округлювати значення до десятих. Ці координати наносимо на координатну площину. Спробуємо прочитати по рисунку властивості цієї функції.

Побудова графіка функції

Учні Графік проходить через початок координат. Значення аргументу невід'ємні, тобто областю визначення функції є множина невід'ємних чисел. Функція  теж невід’ємна, тобто областю значень функції – множина  невід'ємних чисел.

Учитель Порівняйте значення функції при х =4 і х = 9.

Учні  При збільшені значення аргументу збільшується значення функції.

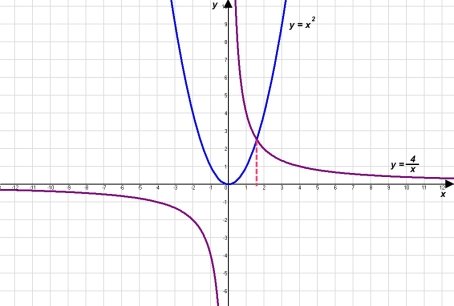
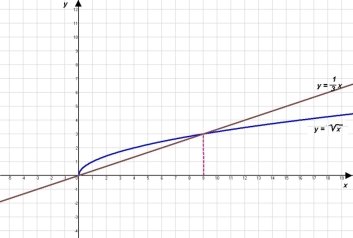
Учитель Подивіться на зображення 2, що ви бачите там?

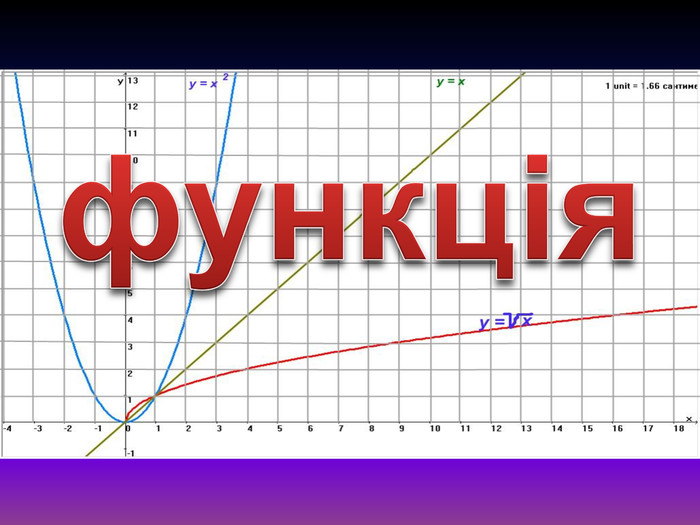
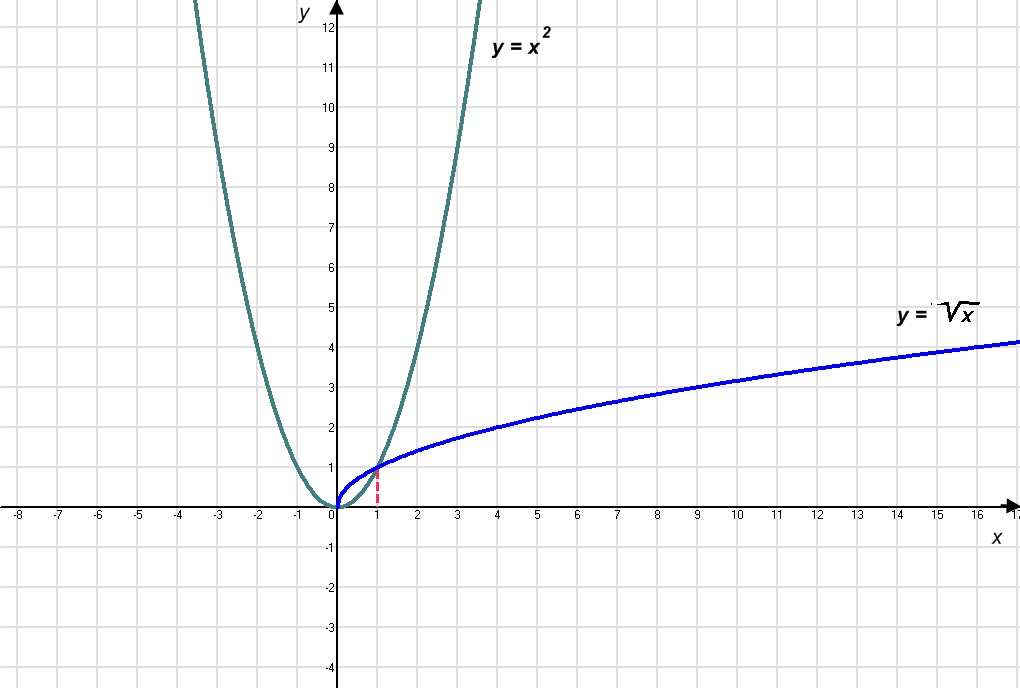
Учні  Графіки трьох функцій. Пряма у = х, парабола  у = х²  і графік функції  .

Учитель Уважно придивіться до цих графіків, чи не можете встановити якийсь зв'язок між ними. Спробуйте перегнути малюнок по прямій, що ви помітили?

Учні  Вітка параболи співпала з графіком функції  . Мабуть вони симетричні відносно цієї  прямої.

Учитель Так. Кажуть, що графіком функції   є ліва гілка параболи у = х², повернута на 90° вправо. Всі ці властивості, що ми зараз з вами прочитали по графіку, ви знайдете на сторінці 182 вашого підручника.

Робота з підручником.

Учитель А зараз виконаємо такі завдання.

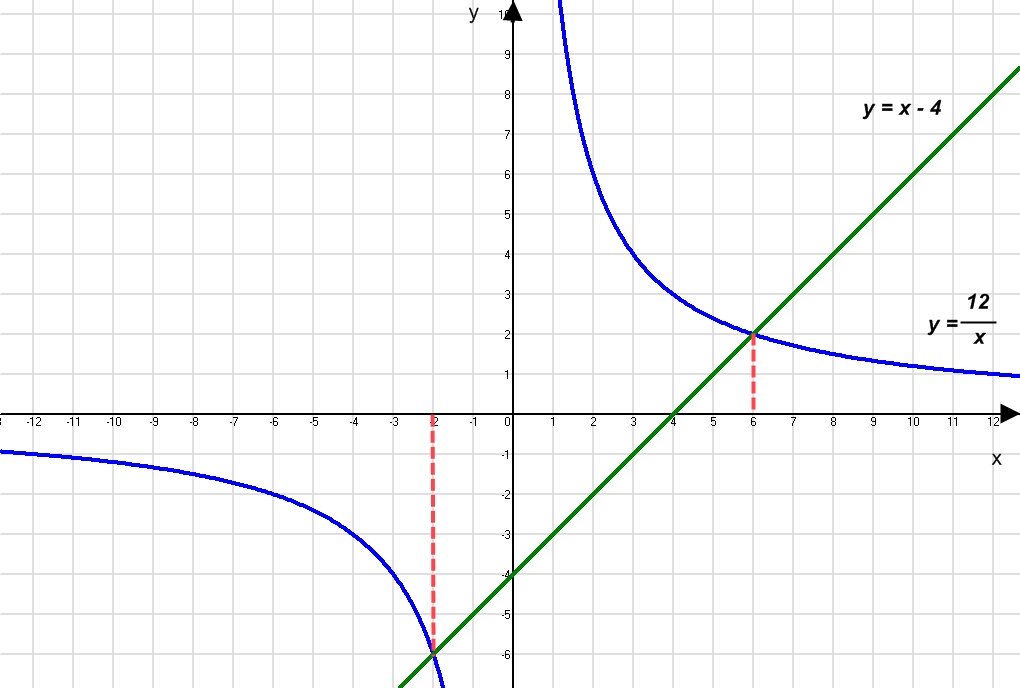
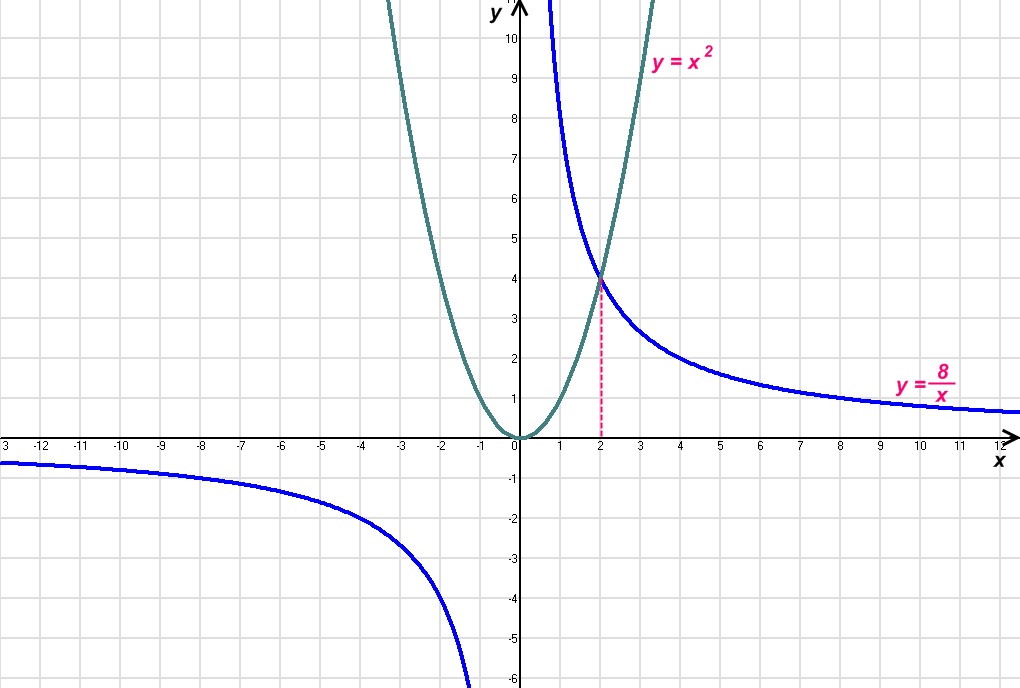
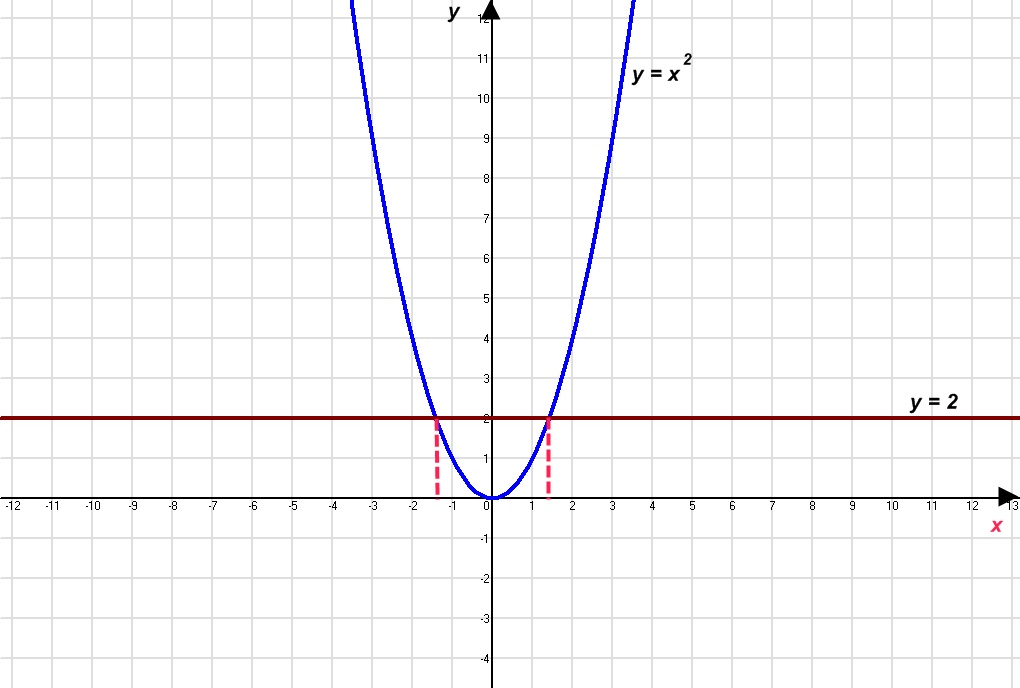
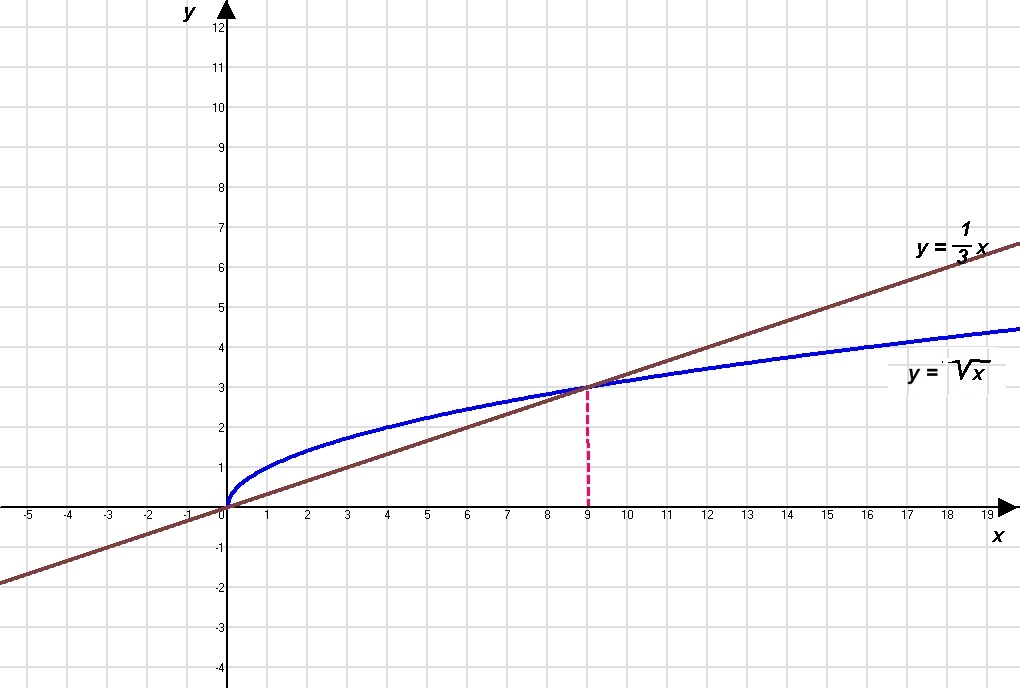
Розв’язати графічно такі рівняння:

Оцінювання зробленого завдання

ІV. Підсумок уроку

Які властивості вивченої функції ви запам’ятали?

V. Домашня робота

Вивчити  властивості функції .