Урок геометрії 7 клас

Урок геометрії у 7 класі

«У світі геометрії»

Підготувала:

Учитель математики

СЗШ І - III ст. №1

м. Хмільника

Покотилова Ірина Миколаївна

2009р.

Мета : ознайомити учнів з історією виникнення геометрії; з першими геометричними поняттями: точка і пряма, «лежати між»(«лежати на») для точок прямої з їх умовними позначеннями; з простішими фігурами на площині; розвивати інтелектуальні якості особистості школяра такі, як самостійність, здібність до узагальнення; формувати вміння чітко і ясно викладати свої думки; прививати інтерес до предмету.

Тип уроку: комбінований з використанням комп'ютерних технологій (показ слайдів ).

ХІД УРОКУ

І. Слово вчителя

На початку XX століття великий французьський архітектор Ле Корбюз'є сказав: «Я думаю, що ніколи до сьогодення ми не жили в такий геометричний період. Все навкруги - геометрія».

Ці слова точно характеризують і наш час. Світ, в якому ми живемо, насичений геометрією будинків, вулиць, гір і полів, витворами природи і людини. Краще орієнтуватися в ньому допоможе предмет - геометрія, який ми починаємо вивчати з цього уроку.

Уважно прочитайте тему уроку, поміркуйте над ії формулюванням і сформулюйте питання, на які ми повинні, на ваш погляд, дати відповіді на протязі уроку.

Учні називають питання, а учитель обіцяє, що на всі питання будемо намагатися відповісти всі разом, протягом уроку.

Питання, які можуть виникнути:

•     Що таке «геометрія»?
•     Коли і з якою метою зародилась наука - геометрія?
•     Хто перший привів у систему відомості про геометрію та її основні положення?
•     Що вивчає геометрія?
•     Як можна пояснити, що таке точка, пряма, відрізок?

Запрошую вас відвідати світ геометрїї(слайд, 1)

• Перша сторінка «Начал»

Евкліда. видавництво 1482р.

«Геометрія» - це грецьке слово. Воно означає «землемірство». Така назва зумовлена застосуванням геометрії до вимірювань на місцевості.

Математика, у тому числі й геометрія, є однією з найстародавніших наук. Історія людства налічує понад 2 мільйони років. Вже первісним людям доводилось лічити: треба було визначати, в тій чи іншій групі, давати кількісну оцінку здобичі (м'яса, риби, плодів, поживних коренів) тощо.

Не могли люди не звернути увагу також і на форми речей: щоб виготовити наконечник стріли або списа, видовбати човен із стовбура, треба було придивлятися до відповідних форм камінців, стовбурів дерев тощо. Фіксуючи найприйнятніші форми, люди навчилися виготовляти посуд, пристосування для роботи і полювання, обладнувати житло.

Слайд 2

З розвитком людського суспільства нагромаджувалися знання про форми і властивості цих форм, що сприяло удосконаленню трудових процесів,пов'язаних з будівництвом каналів, городищ і різних за призначенням великих споруд.

Перехід до осілого землеробства висунув проблему вимірювання земельних ділянок. З'явилися й перші фахівці у цій галузі - землеміри. Щоб краще виконувати свої професійні завдання, вони змушені були виявляти і вивчати властивості різних форм та фігур.

Грандіозні єгипетські піраміди, дивовижні споруди в Америці, Індії, Китаї, багатьом з яких по кілька тисяч років, свідчать, що вже в сиву давнину люди багато знали про форми речей і вміло використовували ці знання. Піраміди, які були збудовані більш ніж 5 тисяч років тому, складаються з кам'яних блоків, кожний з яких важить 15 тонн. Ці «цеглинки» так підігнані одна під одну, що між ними неможливо протиснути навіть поштову листівку. А при будівництві використовувались лише найпростіші механізми - ричаги і катки.

Слайд 4

В Вавилоні при розкопках вчені знайшли останки кам'яних стін, висотою в декілька десятків метрів, а висота Вавилонської вежі сягає 82 мерів.

Без математичних знань всі ці споруди неможливо було б збудувати. І все ж математичні знання єгиптян були хаотичними і більше нагадували ряд правил, перевірених на практиці, тому ці правила слід було зазубрювати, не розуміючи чому треба використовувати те, а не інше правило.

Слайд 6

Майже всі великі вчені давнини і середніх віків були видатними геометрами. Девіз академії Платона був

“Та не ввійде сюди ніхто з тих, хто не знає геометрії”

Майже всі великі вчені давнини були видатними геометрами. Девізом стародавньої школи Платона був вислів : «Та не ввійде сюди ніхто з тих,хто не знає геометрії».

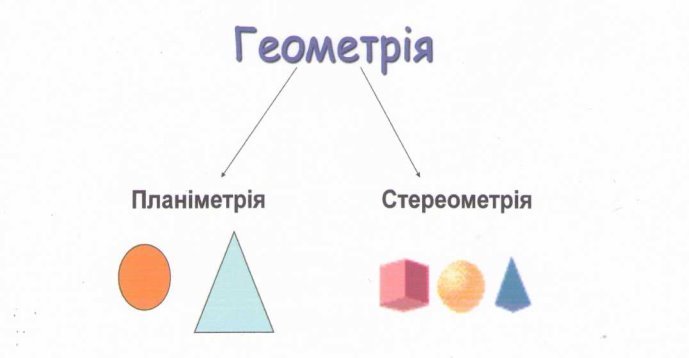
Розташуванням геометричних фігур займаються різні розділи геометрії, такі як: планіметрія (Рlanum (лат) - площина) та стереометрія (Sterio(лат) - тілесний, просторовий). Ми починаємо вивчення геометрії з планіметрії. Планіметрія - це розділ геометрії, в якому вивчаються фігури на площині.

2.     Основні поняття планіметрії

Слайд 9

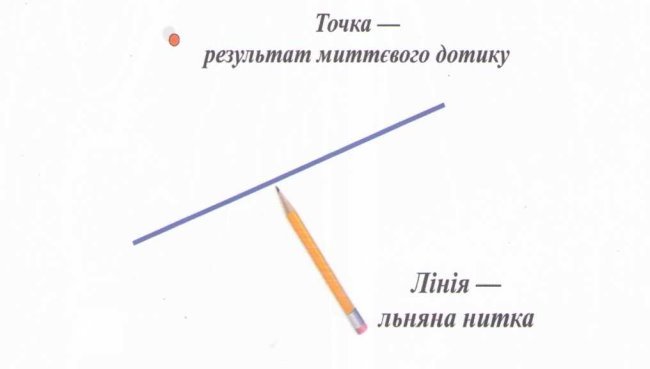
Як будинок складається з цеглинок, так і геометричні фігури складаються з найпростіших фігур. Звичайно, сама головна - це точка. Термін «точка» походить від дієслова «ткнути», первісний зміст - наслідок миттєвого уколу.

Термін «лінія» походить від латинського Іinea, що означає «льняна нитка».

3.    Повторення відомостей про точки і прямі, і їх розташування відносно один одного.

•        Давайте, пригадаємо, як прийнято позначати точки і прямі.

Точки прийнято позначати великими латинськими літерами А, В, С,...

Прямі позначаються малими латинськими літерами: а, Ь, с, сі,...

Існує певне розташування прямих і точок, а саме: точки можуть лежати на прямій або ще кажуть належати прямій, а можуть не належати прямій. Той факт,що точка належить прямій можна записати за допомогою символа належності «Є». Тобто, якщо точка належить прямій а, то пишуть т.А Є а. Якщо точка не належить прямій одо пишуть т.А а.

• Основні властивості належності точок і прямих:
  

• Давайте проведемо пряму а і позначимо точку В на ній і точку С поза нею. Скажіть, чи можна ще вказати точку на прямій? (так) Скільки таких точок можна вказати?(безліч) А чи можна вказати ще точки поза прямою?(так) Скільки їх можна вказати?(безліч)
• Отже, який висновок можна зробити про розташування точок і прямих?(Яку б ми пряму не взяли, існують точки, що лежать на прямій і точки, що не лежать на ній)
• Тобто має місце така аксіома:

1. Яка б не була пряма,існують точки, що належать цій прямій, і точки, що не належать їй.

• Давайте позначимо дві точки. Чи можна через них провести пряму?(так) А тепер візьмемо лінійки і спробуємо провести ще одну пряму, яка проходить через ці дві точки. Можете ви це зробити?(ні)
• Якщо не можемо провести більше прямих, то який висновок випливає?(Через будь - які дві точки можна провести тільки одну пряму)
•        Тобто має місце ще одна аксіома:

2.    Через будь - які дві точки можна провести пряму і тільки одну.

• А зараз давайте позначимо три точки , що лежать на одній прямій. Наприклад: А, В, С таким чином:

Слайд 10

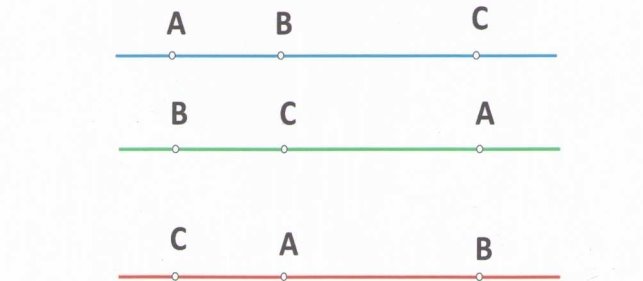
Опишіть малюнок. На першій прямій як розташовані точки ?(А і С «крайні», а між ними точка В) На другій прямій? На третій? Яку закономірність ви помічаєте? (На всіх трьох прямих одна з точок лежить між двома іншими) А якщо візьмемо чотири точки на прямій. Чи буде якась одна точка лежати між двома іншими?(так)

• Який висновок можна зробити? (серед трьох точок, що лежать на прямій одна обов'язково лежить між двома іншими)
•       Отже, має місце ще одна аксіома:

3. Серед трьох точок прямої тільки одна лежить між двома іншими.

•       Пряму можна позначити ще й двома точками, що лежать на ній.

4.   Розв'язування вправ

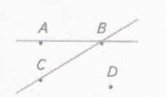
№1. Опишіть, як взаємно розташовані точки і прямі на малюнку (усно).

№2.Позначте в зошиті точки А і В та проведіть через них пряму. Назвіть цю пряму.

№3. Проведіть пряму. Позначте кілька точок, що належать цій прямій, і кілька точок що їй не належать.

№4. Позначте на прямій точки А, В і С так, щоб А і В лежали по один бік від С, а А і С ■ по один бік від В.

5.    Підсумок уроку

Записати мовою математики

1.    Точка М належить прямій а.
2.    Точка N не належить прямій а.

6.    Домашнє завдання

Вивчити : §1, стор.б - 9

Виконати : №10, 15