Стаття "Місце рисункових засобів при вивченні геометрії в 7 класі"

Місце рисункових засобів при вивченні геометрії в 7 класі

 На першому уроці геометрії у 7 класі вчитель знайомить учнів з такими поняттями: геометрія, геометричні фігури, планіметрія, точка, пряма, промінь, основні властивості розміщення точок на прямій. Для закріплення і повторення цих властивостей корисно буде запропонувати учням самостійно виконати геометричні зображення.

 Пояснюючи поняття відрізка, вчителю слід зобразити рисунок та пояснити розміщення точок на прямій (рис. 1). Ми бачимо пряму a і три точки A, B, C на цій прямій. Точка В лежить між точками А і С, вона розділяє точки А і С. Можна також сказати, що точки А і С лежать по різні боки від точки В. Точки В і С лежать по один бік від точки А, вони не розділяються точкою А. Точки А і В лежать по один бік від точки С [5]. Демонстрація рисунком цього пояснення дає можливість чітко сформулювати поняття відрізка.

 

 

 

 

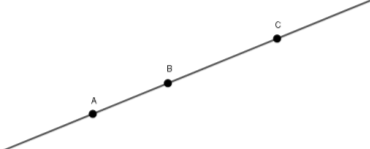
Рис. 1

 Вивчаючи основну властивість розміщення точок відносно прямої на площині, вводимо поняття півплощина за допомогою рисункового засобу (рис. 2). Пряма a розбиває розбиває площину на дві півплощини. Це розбиття має таку властивість. Якщо кінці якого-небудь відрізка належать одній півплощині, то відрізок не перетинає пряму. Якщо кінці відрізка належать різним півплощинам, то відрізок перетинає пряму.

На рисунку 2 точки А і В лежать в одній з півплощин, на які пряма a розбиває площину. Тому відрізок АВ не перетинає пряму a. Точки С і D лежать у різних півплощинах. Тому відрізок CD перетинає пряму a [5].

 

 

 

 

 

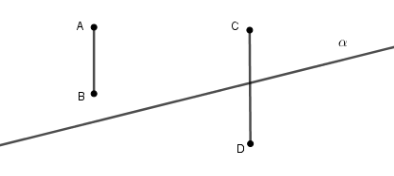
Рис. 2

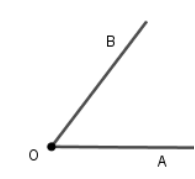 Аналізуючи шкільні підручники з геометрії можна дійти до висновку, що введення поняття кута не є здійсненним без використання рисунка. Проведемо з точки О два промені ОА і ОВ (рис. 3). Дістали відома вам фігуру – кут [5].

 

 

 

 

 

 

Рис. 3

 Трикутник займає досить важливе місце в шкільному курсі планіметрії, оскільки на притаманних трикутнику властивостях базується подальше вивчення курсу геометрії. Зокрема, геометрія плоских прямолінійних фігур – багатокутників, базується на застосуванні різноманітних властивостей трикутників подібно до того, як весь попередній матеріал (пряма, лінія і відрізки, кути) широко використовується при вивченні трикутників.

 Поняття трикутника вводиться конструктивно: як фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки. При цьому, кожен підручник чи методичний посібник закріплює розуміння поняття цієї геометричної фігури допоміжним рисунковим засобом (рис. 4).

 

 

 

 

 

 

 

 

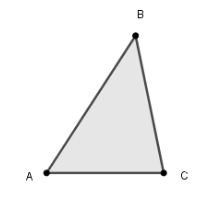
Рис. 2.1.4

 Правильність твердження про властивість тієї чи іншої геометричної фігури встановлюється міркуванням. Це міркування називається доведенням. А саме твердження, яке доводять, називається теоремою [1]. Розглядаючи доведення будь-яких теорем геометрії бачимо, що доцільне їх викладання супроводжується завжди рисунковими засобами. Неможливо пояснити якісно і остаточно зрозуміло без використання рисунків. Наведемо приклад.

 Теорема 1. Якщо пряма, яка не проходить через жодну з вершин трикутника, перетинає одну з його сторін, то вона перетинає тільки одну з двох інших сторін [5].

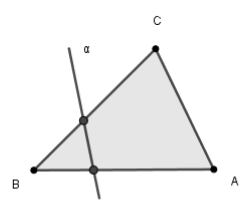 Доведення. Нехай пряма a не проходить через жодну з вершин трикутника АВС і перетинає його сторону АВ (рис. 5). Пряма  a  розбиває

 

 

 

 

 

 

 а) б)

Рис. 5

площину на дві півплощини. Точки А і В лежать в різних півплощинах, оскільки відрізок АВ перетинає пряму a. Точка С лежить в одній з цих півплощин.

 Якщо точка С лежить в одній півплощині з точкою А, то відрізок АС не перетинає пряму a, а відрізок ВС перетинає цю пряму (рис. 5, а).

 Якщо точка С лежить в одній півплощині з точкою В, то відрізок АС перетинає пряму a, а відрізок ВС не перетинає її (рис. 5, б).

 В обох випадках пряма a перетинає тільки один з відрізків АС або ВС. Оце і усе доведення [2].

 Вивчення теми «Суміжні і вертикальні кути» починається з означення суміжного кута, яке сприймається за допомогою рисункового засобу. А в підручнику М. І. Бурди, Н. А. Тарасенкової «Геометрія» це означення подається після розгляду рисунка.

 Побудуємо кут АОВ і проведемо доповняльний промінь до однієї з його сторін, наприклад ОС (рис. 6). Утворилося два кути – АОВ і СОВ. У них сторона ОВ – спільна, а сторони ОА і ОС – доповняльні промені. Такі кути є суміжними [2].

 

 

 

 

 

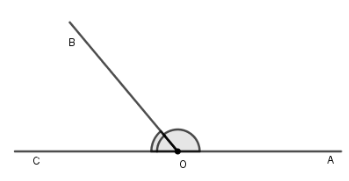
Рис. 6

 Така ж методика вивчення означення вертикальних кутів наводиться в цьому підручнику: починаючи з розгляду та характеристики рисунка і підводячи учнів до самого означення.

 Закінчуючи вивчення теми «Суміжні і вертикальні кути» О. В. Погорєлов в своєму підручнику «Геометрія» 7-9 класи подає параграф «Що потрібно робити, щоб добре встигати з геометрії», в якому окреслює такі рекомендації: «Корисно зробити від руки рисунок фігури, означення якої маєте дати. Якщо у запитанні йдеться про теорему, сформулюйте її, з’ясуйте, в чому полягає умова і висновок теореми. Зробіть від руки рисунок, який ілюструє зміст теореми» [5].

 Теорема 2. У рівнобедреному трикутнику кути при основі рівні [5].

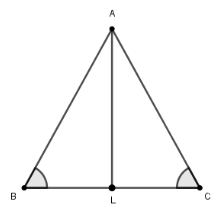 Доведення. Нехай АВС – рівнобедрений трикутник з основою ВС (рис. 7). Проведемо бісектрису АL, яка розіб’є його на трикутники ABL і ACL.

 

 

 

 

 

 

 

Рис. 7

Оскільки АВ = АС, AL – спільна сторона, BAL = CAL, то за двома сторонами і кутом між ними АВL = ACL. Із рівності цих трикутників випливає, що В = С, тобто кути при основі трикутника АВС – рівні.

 Вивчення та рисункові засоби теми «Геометричні побудови» являються основою для засвоєння принципів та методів зображення більш складних форм. Введення таких понять, як коло, центр кола, радіус кола, хорда, діаметр, дотична до кола здійснюється за допомогою рисунків.

 Головним підґрунтям цієї теми є задачі на побудову (побудова трикутника з даними сторонами; побудова кута, що дорівнює даному; побудова бісектриси кута; ділення відрізка пополам; побудова перпендикулярної прямої; геометричне місце точок).

 У задачах на побудову йдеться про побудову геометричної фігури за допомогою даних креслярських інструментів. Такими інструментами найчастіше є лінійка і циркуль. Розв’язування задачі полягає не стільки в побудові фігури, скільки у знаходженні способу, як це зробити, і відповідному доведенні. Задача вважається розв’язаною, якщо знайдено спосіб побудови фігур і доведено, що в результаті виконання зазначених побудов справді виходить фігура з потрібними властивостями [1].

 Наведемо кілька цікавих планіметричних задач.

 Задача 1. Три точки Q, S і R лежать на одній прямій. Точка P розміщена так, що QPS = 12 і PQ = PS = RS (рис. 8). Знайдіть QPR [3].

 

 

 

 

 

 

 

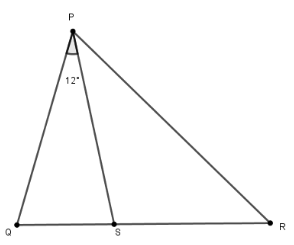
Рис. 8

 Розв’язання. Оскільки QP = PS, то QPS рівнобедрений і PQS =            = PSQ = = 84. Тоді PSR = 180 – 84 = 96, а якщо PS = SR, то      PSR рівнобедрений і SPR = SRP = = 42, тоді QPR =             = QPS + SPR = 54.

 Задача 2. Нехай М – точка перетину бісектриси кута С і серединного перпендикуляра до сторони АВ прямокутного трикутника АВС (рис. 9); K, L, N – основи перпендикулярів, опущених із М на сторони трикутника. Тоді трикутники AMK і BMK рівні за двома катетами, і тому АМ = ВМ. Трикутники CLM і CNM рівні за гіпотенузою і двома кутами, тому LM = MN, CL = CN. Тоді трикутники ALM і MNB рівні за гіпотенузою і катетом, тому AL = BN. Тоді      AC = AL + LC = BN + NC = BC, тобто у прямокутному трикутнику катет і гіпотенуза рівні? [4]

 

 

 

 

 

 

 

 

 

 

 

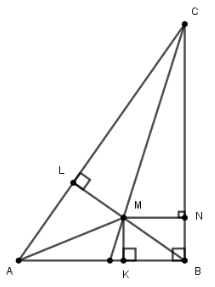
Рис. 9

 Розв’язання. У цьому парадоксі немає жодної логічної помилки, є неправильно виконаний рисунок.

 Продовжимо бісектрису СМ до перетину зі стороною АВ в точці С₁. За властивостями бісектриси, . Оскільки АС  ˃ СВ, то ˃ 1, тобто      АС₁ ˃ С₁В і точка С₁ лежить між точками K і В, тобто серединний перпендикуляр до сторони АВ і бісектриса кута С перетинаються зовні трикутника АВС.

 Задача 3. Нехай точка K (рис. 10) належить стороні АВ трикутника АВС, причому відрізок СK перетинає його бісектрису BF в такій точці Q, що              BQC = 2 BFA і BAF = 2 CQF. Довести, що KF = FC [6].

 

 

 

 

 

 

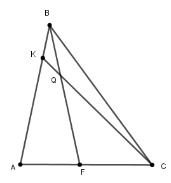
Рис. 10

Розв’язання. Позначимо BAF = , ABC = , BFA = φ. Тоді   BQC = = 2φ, CQF = .

З трикутника ABF маємо: φ = 180 –   –  . Також маємо: BQC +          + FQC = 2φ + = 180. Звідси отримуємо: φ = +  .

З трикутника BKQ маємо: BKQ = 180 –  –  . Також маємо: BFC = = 180 – φ = 180 –  –  . Оскільки з точок K і F відрізок BC видно під рівними кутами, то навколо чотирикутника BCFK можна описати коло.

Оскільки BF – бісектриса KBC, то KF = FC як хорди дуг, що відповідають рівним вписаним в це коло кутам.

Отже, використання рисункових засобів при вивченні понять, означень, теорем, властивостей та аксіом допоможе учням успішно засвоїти геометричний матеріал у 7 класі, підвищить їх інтерес до математики.

Список використаної літератури

1. Бевз Г. П. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова. – К.: Вид-во «Відродження», 2015. – 192 с.
2. Бурда М. І. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закл. /              М. І. Бурда, Н. А. Тарасенкова. – К.: Видавничий дім «Освіта», 2015. – 208 с.
3. Міжнародний математичний конкурс «Кенгуру – 2005»: Інформ. вісник / Уклали: А. С. Добосевич, М. С. Добосевич, Р. Є. Кокорузь, Х. Р. Трущак. – Львів: Каменяр, 2005. – 67 с.
4. Міжнародний математичний конкурс «Кенгуру – 2011»: Інформаційний вісник / Кенгуру – 2011, міжнародний математичний конкурс; уклали:        А. С. Добосевич, М. С. Добосевич, О. М. Добосевич, Р. Є. Кокорузь,           О. Б. Таратула. – Львів: Каменяр, 2011. – 54 с.
5. Погорєлов О. В. Геометрія: Планіметрія: Підруч. для 7-9 кл. загальноосвіт. навч. закл. – 7-ме вид. – К.: Школяр, 2004. – 240 с.
6. Сарана О. А. Математичні олімпіади: просте і складне поруч: Навч. посібник. 2-ге видання, доп. – Тернопіль: Навч. книга – Богдан, 2011. –     400 с.