Урок геометрії 8 клас на тему "Теорема Фалеса Середня лінія трикутника

Тема. Теорема Фалеса. Середня лінія трикутника

Мета: формувати в учнів усвідомлене розуміння змісту теореми Фалеса та способу її доведення; формувати вміння відтворювати фор­мулювання теореми Фалеса; застосовувати її для розв'язування задач на знаходження довжин відрізків, що відтинаються на сторонах пара­лельними прямими; розв'язувати задачі на поділ відрізка на п рівні відрізки або в даному відношенні. сформувати в учнів поняття середньої лінії трикутника. Роз­глянути властивості середньої лінії трикутника розвивати вміння робити висновки  культуру математичних записів виховувати інтерес до математики  упевненість у власних силах

Тип уроку: засвоєння нових знань.

 Обладнання : конспект підручник (Геометрія 8 клас  Єршова Голобородько) роздатковий  матеріал

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Самостійна робота

Варіант 1

1. Основи рівнобічної трапеції дорівнюють 9 см і 15 см. Знайдіть від­різки, на які ділить більшу основу висота, проведена з вершини ту­пого кута.
2. У рівнобічній трапеції один з кутів дорівнює 120°. Діагональ тра­пеції утворює з основою кут 30°. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 8 см.

Варіант 2

1. Основи рівнобічної трапеції дорівнюють 2 см і 10 см. Знайдіть дов­жини відрізків, на які висота трапеції, проведена з вершини тупого кута, ділить більшу основу.
2. У рівнобічній трапеції одна основа дорівнює а, друга втричі менша. Кут при більшій основі дорівнює 60°. Визначте периметр трапеції.

 

III. Формулювання мети і завдань уроку

IV. Актуалізація опорних знань

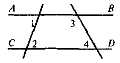
Виконання усних вправ за готовими рисунками

1		Дано: 1 = 2. Довести: 3 + 4 = 180°
2		Дано: ВО = ОD, 1 = 2. Довести: ΔAOD = ΔCOB
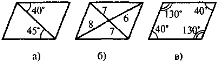
3		Які помилки допущено в зображенні парале­лограма

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V. Засвоєння знань

План вивчення нового матеріалу

1. «Класичне» формулювання і доведення теореми Фалеса.
2. інше формулювання теореми Фалеса.
3. Задача про поділ відрізка на п рівних частин.

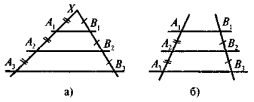
Теорема Фалеса
		Паралельні прямі, які пе­ретинають дві інші сторо­ни кута і відтинають на одній із них рівні відрізки, відтинають рівні відрізки і на іншій сто­роні
Узагальнена теорема Фалеса
			Паралельні прямі, які пе­ретинають сторони кута, відтинають на сторонах цього кута пропорційні відрізки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

VI. Формування первинних умінь

Виконання усних вправ №169    170    171    172 

1. Чи може середня лінія трикутника бути перпендикулярною до його сторони; до двох його сторін?
2. Чи можуть середні лінії трикутника дорів­нювати 3 см, 4 см і 10 см? Чому?

Виконання письмових вправ

Робота з підручником № 178  182 колективно

№180-індивідуально

VII. Підсумки уроку

Бліц-опитування

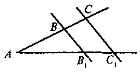
Які помилки допущено в зображенні середньої" лінії трикутника (див. рис. 3)?

 

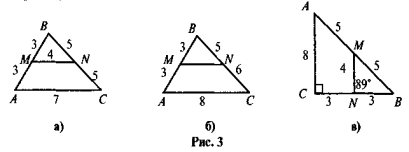
VIII. Домашнє завдання

Вивчити зміст нового теоретичного матеріалу.

§6   п 6.1  6.2  № 179  181