Урок геометрії 8 клас "Розв’язування прямокутних трикутників. Прикладні задачі"

Урок №4

Тема: Розв’язування прямокутних трикутників. Прикладні задачі

Мета:

• систематизувати знання з теми «Розв’язування прямокутних трикутників»;
• розвити вміння застосовувати набуті знання у реальному житті;
• виховання активності, уваги, кмітливості, самостійності. Прищеплення інтересу до математики.

Тип уроку: узагальнення та систематизації знань

Хід уроку

І. Організаційний момент

• перевірка готовності учнів до уроку;
• у журналі фіксуються відсутні.

ІІ. Перевірка домашнього завдання

• За розданими вказівками учні – помічники перевіряють правильність виконання домашнього завдання.

№614

1. Дано: прямокутний трикутник, а = 34 см, .

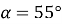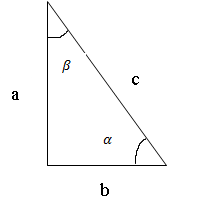Знайти: с, b, .

Розв’язання.

За властивістю кутів прямокутного трикутника:

с =  а : = 34 : 0,819 см.

b = с = 42  0,574 см.

Відповідь: 35°, 42 см, 24 см.

2. Дано: прямокутний трикутник, с = 16 см, .

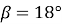Знайти: а, b, .

Розв’язання.

За властивістю кутів прямокутного трикутника:

.

а = с  = 16  0,951 см, b = с  = 16  0,309 5 см.

Відповідь: 72°, 15 см, 5 см.

3. Дано: прямокутний трикутник, b =12 см, с = 13 см.

Знайти: а, .

Розв’язання.

За теоремою Піфагора: с² = а² + b². Звідси а² = с² – b²; а² = 13² – 12²;

а² = 169 – 144; а² = 25; а = 5 см. Кути знайдемо за тригонометричними функціями:

; . Тоді за властивістю кутів прямокутного трикутника: .

Відповідь: 23°, 67°, 5 см.

4. Дано: прямокутний трикутник, b =14 см, а = 4 см.

Знайти: с, .

Розв’язання.

Кути знайдемо за тригонометричними функціями:

. Тоді за властивістю кутів прямокутного трикутника: . Гіпотенузу знайдемо так: с =а : , с = 4 : 0,276 см.

Відповідь: 16°, 74°, 14,5 см.

№ 620

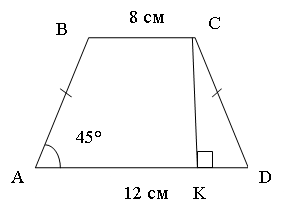Дано: ABCD – трапеція, AB = CD, AD = 12 см,

BC = 8 см, , СК – висота.

Знайти: CD і СК.

Розв’язання.

Оскільки трапеція рівнобічна, то

 

KD =  , KD = . Тоді з

прямокутного трикутника CKD: CD = KD : , CD = 2 : ; CD = см; СК = КD = 2 см (бо якщо то за властивістю кутів прямокутного трикутника )

Відповідь: 2 см і см.

№ 622.

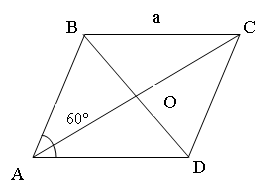     Дано: ABCD – ромб, ВС = а,

Знайти: АС і BD.

Розв’язання.

 

За властивістю діагоналей ромба: АС – бісектриса , т.О – середина АС і BD, . Тоді з прямокутного трикутника АОВ (АВ = а):

ВО = АВ  = а, АО = АВ  = . Звідси BD = a, AC = .

Відповідь:  , а.

ІІІ. Актуалізація опорних знань

Розминка «Вірю – Невірю»

1. Чи правильно, що теорема в перекладі з грецької мови означає ”вистава” ? (так)
2. Чи правильно, що центр кола, описаного навколо прямокутного трикутника є серединою гіпотенузи? ( так)
3. Чи правильно, що sin 60^о = 0,5? (ні)
4. Чи правильно, що sin²В + cos²В = 1?  (так)
5. Чи правильно, що гіпотенуза дорівнює добутку катета на синус протилежного кута? (ні)

IV. Оголошення теми і мети уроку

Сьогодні ви переконаєтесь у доцільності і корисності вивчення прямокутних трикутників, розглянувши задачі, які ставить нам життя.

V. Розв’язування задач

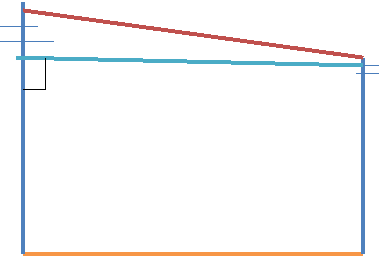
№1. Висоти двох вертикальних стовпів дорівнюють 5м і 12,5м. Відстань між ними 10м. Знайти найменшу довжину троса, яким можна з’єднати верхні кінці стовпів?

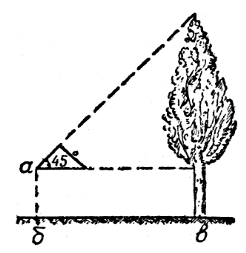
№2. Знайти висоту дерева, якщо з відстані 5 метрів людина бачить його під кутом 45 градусів.

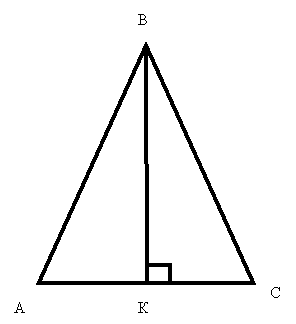
№3. Ширина будинку 7 м,  довжина крокви 4,5 м. Під яким кутом крокви нахилені до стелі ?

Дано: АС = 7 м, АВ = ВС = 4,5 м. Знайти кут А.

 

 

 

 

 

 

 

 

 

 

№4. Вершину дерева, віддаленого від даного пункту на 16 м, видно під кутом 16º до горизонту , а вершину другого дерева віддаленого від цього самого пункту на 24 м, видно під кутом 19º. Яке дерево вище і на скільки?

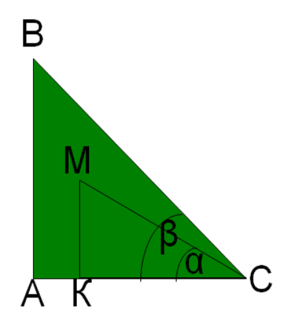
Дано: АС = 24 м, КС = 16 м, .

Знайти: АВ – КМ.

Розв’язання.

АВ=АСtgβ ;       КМ=КСtgα .

АВ=24·0,344=8,256м.      КМ=16·0,287=4,592м

АВ-КМ=3,664м.

Відповідь:3,664 м.

 

 

№5. Ескалатор метрополітену має 17 сходинок від підлоги наземного вестибюля до підлоги підземної станції. Ширина сходинок 40 см, висота 30 см. Визначте: а) довжину всіх сходинок; б) кут їх нахилу; в) глибину станції по вертикалі.

 

 

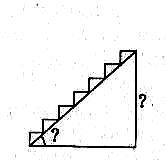
Розв’язування.

У кожному маленькому прямокутнику на рисунку знайдемо довжину гіпотенузи: см. Таких відрізків 17. Отже, довжина сходинок 50  17 = 850 (см) =     85 дм. Глибина станції по вертикалі:  30  17 = 510 (см) = 51 дм. Тоді кут нахилу сходинок знайдемо так: ; α = 37°.

Відповідь: 85 дм, 51 дм, 37°.

№617 – підручник.

VI. Підсумок уроку

VII. Домашнє завдання

Виконати: №616, 618, 624