Урок геометрії 8 клас "Співвідношення між сторонами і кутами прямокутного трикутника. Значення синуса, косинуса і тангенса деяких кутів"

Урок №2

Тема: Співвідношення між сторонами і кутами прямокутного трикутника.  Значення синуса, косинуса і тангенса деяких кутів   

Мета:

• сформувати вміння учнів знаходити невідомі сторони прямокутного
• трикутника, використовуючи sin, cos, tg, гострого кута; знайти значення синуса, косинуса і тангенса для кутів 30°, 45°, 60°.
• розвивати обчислювальні навички, мислення;
• виховувати відповідальне ставлення до навчання, наполегливість.

Тип уроку: засвоєння нових знань, вмінь та навичок.

Хід уроку

І.  Організаційний етап

ІІ. Перевірка домашнього завдання. Актуалізація опорних знань учнів

№ 582

Розв’язання.

За т. Піфагора:

АВ = (см)

1)

2)

3) .

Решта завдань перевіряється за  розданим зразком.

1. Що можна сказати про катет прямокутного трикутника, протилежний куту 30°?
2. Чому дорівнюють гострі кути рівнобедреного прямокутного трикутника?
3. Чому дорівнюють кути рівностороннього трикутника?

ІІІ. Формулювання теми та мети уроку

• Сьогодні ми навчимось виражати з формул синуса, косинуса і тангенса гострого кута прямокутного трикутника катети та гіпотенузу, використовуючи властивість пропорції, а також знаходити значення даних тригонометричних функцій найбільш поширених кутів: 30°, 45°, 60°.

ІV. Вивчення нового матеріалу

     Записати правила знаходження синуса, косинуса і тангенса кута В (домашнє  завдання №582). Виразити з цих рівностей катети та гіпотенузу і сформулювати правила їх знаходження. Записати правила за зразком:

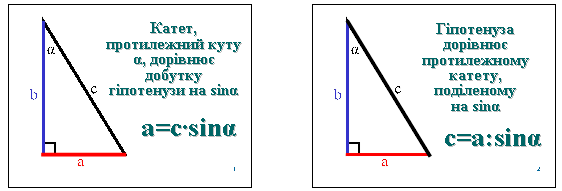
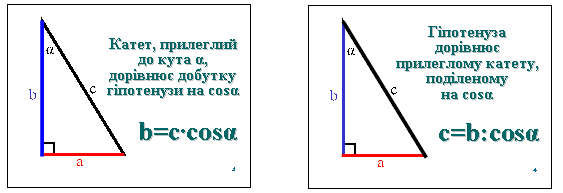
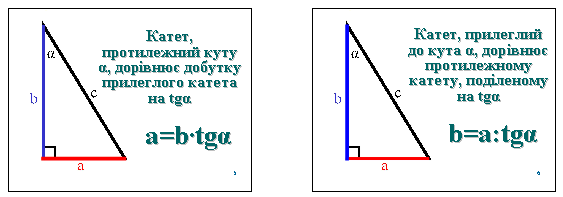
Групова робота: учні розподіляються на три групи. Перша визначає , друга - , третя - . Кожна група поступово заповнює відповідний рядок у таблиці:

1)

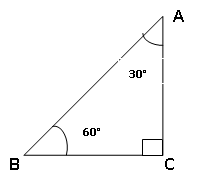
Як відомо, у прямокутному трикутнику проти кута 30° лежить катет, у два рази менший за гіпотенузу, тому якщо АВ = с, то ВС = . Тоді АС = = . Тоді 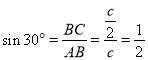 ; ; tg30° =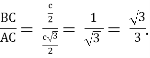

2)

Розглянемо рівнобедрений прямокутний трикутник АСВ (), тоді його кути дорівнюють 45°. Нехай його катети дорівнюють а, тоді АВ =   ; ;

tg45° =

3)

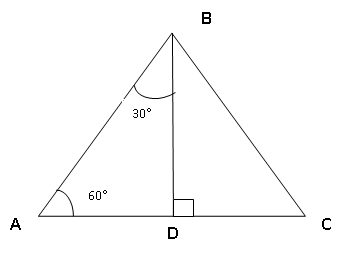
Розглянемо рівносторонній трикутник, проведемо в ньому медіану BD, яка є бісектрисою і висотою. Тому трикутник ADB – прямокутний з гострим кутом 30° при вершині В. Якщо а – сторона рівностороннього трикутника, то AD = , тоді BD = . ; ; tg 60° = .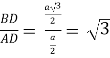

• Зверніть увагу на те, що 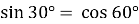; ; 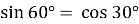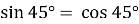, тобто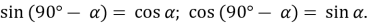

V. Первинне закріплення нових знань учнів

    Розв’язати задачі №607(1,3,5). Учні виконують завдання на дошці використовуючи малюнок та  записані у зошитах формули.

№609, 611, 613(2,4), 619

VIІ.  Підсумки уроку

• Як можна знаходити катети і гіпотенузу прямокутного трикутника, без використання теореми Піфагора?
• Чому дорівнюють синус, косинус і тангенс кута 30°?
•   Чому дорівнюють синус, косинус і тангенс кута 45°?
• Чому дорівнюють синус, косинус і тангенс кута 60°?

VІ.  Домашнє завдання

Вивчити: п.18, ст.131

Виконати: №608, 610, 612.