Урок геометрії у 7 класі "Співвідношення між сторонами і кутами трикутника. Нерівність трикутника"

 

 

 

 

 

 

 

Урок геометрії у 7 класі

«Співвідношення між

сторонами і кутами трикутника.

Нерівності трикутника»

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку. Співвідношення між сторонами і кутами трикутника. Нерівності трикутника.

Мета:

навчальна: сформулювати теорему про співвідношення між сторонами і кутами трикутника, розуміння і засвоєння нерівності трикутника; розвивальна: розвивати вміння, які передбачають застосування цих теорем,  увагу, інтелектуальні здібності учнів, уміння аналізувати та робити висновки; виховна: виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу.

формування ключових компетентностей: інформаційної, комунікативної, пізнавальної, творчої.

Тип уроку: засвоєння нових знань, формування вмінь.

Обладнання: проектор, набір креслярських інструментів, роздатковий матеріал, підручник.

Хід уроку

І. Організаційний етап.

ІІ. Повідомлення теми і завдань уроку. Мотивація діяльності учнів.

Багатьом відома така притча.

Звернувся до ченця бідняк:

- Дай мені рибу. Я голодний.

Чернець мовчки віддав вудку.

Повчальний характер притчі зрозумілий: треба давати не стільки їжу, скільки спосіб її добувати.

Цей висновок,  безпосередньо, стосується цілей і завдань нашого уроку. Тему уроку ви дізнаєтеся, якщо виконаєте наступне завдання: (слайд 2)

- розв'яжіть анаграми (у словах змінено порядок букв). Які слова зашифровані?
1.укт (кут)
2.тосроан (сторона)
3.китнкутри (трикутник)
4.свяпвішіоннедн              (співвідношення)

5. енстьнівір                         (нерівність)
    Якщо об’єднати отримані слова, отримаємо тему уроку. (Співвідношення між сторонами і кутами трикутника. Нерівність трикутника). (слайд 3)

Сьогодні ми  встановимо ще дві властивості, які має трикутник та навчимося застосовувати вивчені властивості до розв’язування різних задач. Отже, відкрийте зошити і запишіть тему уроку: «Співвідношення між сторонами і кутами трикутника. Нерівність трикутника». Крім того, на уроці ми будемо використовувати метод «Шести капелюхів». У процесі вирішення практичних завдань ми будемо «приміряти» 6 незалежних типів мислення.  

Отже, починаємо роботу. Я хочу, щоб епіграфом нашого уроку стали такі слова «Скажи мені – я забуду. Покажи мені – я запам’ятаю. Залучи мене – я навчусь»   (східна приказка) (Слайд 4).

Протягом вивчення розділу «Трикутники», ми створювали «Дерево знань». Сьогодні ми доповнимо «дерево» новими властивостями, які має трикутник.

ІІІ. Актуалізація опорних знань.

1. Метод «Картинна галерея». 

А допоможе нам сьогодні на уроці Ваш улюблений телефон. Справа в тому, що для того щоб виконати необхідне завдання, спочатку, потрібно розшифрувати дану інформацію, скористатися сканером QR-кодів. (слайд 5)

Завдання полягає в тому, щоб співставити зображення трикутника з його назвою. (слайд 6)

Продовжимо далі.

     3) Самостійна тестова робота.

 (слайд 7, після розкодування)

1. Який кут називається зовнішнім?

Є) кут, сторони якого є доповняльними променями;

Е) кут, суміжний із внутрішнім кутом трикутника;

Ж) кут, між продовженнями двох сторін трикутника.

2. Який трикутник називають рівнобедреним?

 П) трикутник, у якого всі кути гострі;

 Р) трикутник, у якого всі сторони рівні;

С) трикутник, у якого дві сторони рівні.

3. Яка властивість бісектриси рівнобедреного трикутника?

Б) бісектриса, проведена до основи, є висотою та медіаною рівнобедреного трикутника;

В) бісектриса ділить протилежну сторону навпіл;

Г) бісектриса ділить кут на два рівні відрізки.

4. Яка властивість кутів рівнобедреного трикутника?

     І) кути при основі рівні;

     К) всі кути рівні;

     Л) всі кути по 60°.

5. Який трикутник називається прямокутним?

    З) трикутник, у якого всі кути прямі;

    І) трикутник, у якого всі сторони перпендикулярні;

    К) трикутник, у якого один кут прямий.

 

Перевіримо, що у вас вийшло: Е, С, Б, І, К. (слайд 8)

Завдання: переставте букви місцями,  додайте ще п’ять букв і вийде слово, яке є елементом трикутника. (бісектриса)

ІV. Вивчення нового матеріалу.

Продовжуємо роботу. У кожного з вас є картка із зображеним на ній трикутником. (слайд 9)

Завдання 1.

- Виміряти довжини  сторін і градусні міри кутів  трикутника.

- Порівняти довжини сторін із мірами протилежних  до них кутів?

 

Який висновок ви можете зробити, провівши дане дослідження?

У трикутнику:

1) проти більшої сторони  лежить більший кут, і навпаки,  проти більшого кута

  лежить більша сторона. (слайд 10)

(робимо відповідні записи у зошиті)

Доведення теореми:

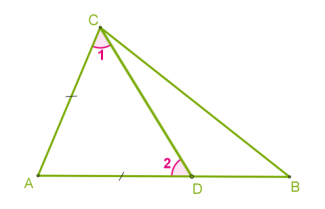
Нехай у ∆АВС сторона АВ>АС.

Доведемо, що∠ C >∠ B.

 1) 1. Відкладемо на стороні AB відрізок, рівний стороні AC.

△CAD — рівнобедрений. (∠ 1 =∠ 2).

 2. Оскільки AD<AB, то точка D лежить між точками A і B.

Отже, кут 1 є частиною кута C і, відповідно:
 ∠ C>∠ 1.

 3. Кут 2 — зовнішній кут трикутника BDC, тому ∠ 2>∠ B.

 ∠ 1=∠ 2 (оскільки це кути при основі рівнобедреного трикутника ADC)

 Отже, ∠ C>∠ 1=∠ 2>∠  B.              

 Звідси випливає, що ∠ C >∠ B.

2) Нехай у ∆АВС кут ∠C >∠ B.

Доведемо від супротивного,  що  АВ>АС.

Припустимо, що це не так, тоді АВ=АС або АВ<АС. У першому випадку ∆АВС – рівнобедрений з основою ВС, тобто ∠ C =∠ B. У другому випадку за щойно доведеним  ∠ C <∠ B. В обох випадках маємо суперечність із умовою ∠ C >∠ B. Отже,  наше припущення хибне, тобто АВ>АС.

 (Створення проблемної   ситуації).

 Продовжуємо далі.  Ми отримали повідомлення  з інтернет-магазину   Аliexpress. (слайд 11)

   Деякий добродій Х захотів розбагатіти і почав продавати земельні ділянки, які мають форму трикутників. Продав 3 ділянки розміри яких: 2м, 4м, 6м; 1м, 3м, 5м і 3м, 5м, 7м. Але люди, які купили перші дві ділянки, прийшли з претензіями, що таких ділянок не існує.

Давайте з’ясуємо, чому виникла така ситуація?  (слайд 12)

Дослідницька робота (Слайд 13) (на парті учні мають по 3 трубочки)

Завдання 2.

- Виміряйте довжини трубочок і складіть з них трикутник. Чи утворився у вас трикутник?

- Порівняйте довжину кожної  сторони трикутника із сумою двох інших сторін.

Запитання вчителя: (слайд 14)

• Чи справилась із своїм І група? (трикутник зі сторонами 7см, 12см, 9см)   Так.
• Чи побудували трикутник зі сторонами 7см, 14см, 7см учні ІІ групи?  Ні.
• А третя група змогла побудувати трикутник зі сторонами 5см, 16см, 7см?  Ні.
• Чи побудувала четверта група трикутник зі сторонами 15см, 8см, 11см?  Так.

Від чого  залежить  можливість    побудови  трикутника? (Від довжин його сторін).

Який висновок можна зробити? (Кожна сторона трикутника менша  від суми двох інших  його сторін). Кожну із цих трьох нерівностей називають нерівністю трикутника. (слайд 15)

(робимо відповідні записи у зошитах, доведення теореми розглянете вдома самостійно)

Як ви думаєте, обов’язково перевіряти всі три сторони? Достатньо порівняти більшу сторону трикутника із сумою двох інших. (слайд 16)

(Отже, тепер зрозуміло чому виникла така ситуація з ділянками, не всі  трикутники з такими сторонами існуватимуть).(6=2+4, 5>1+3) (слайд 17)

Працюємо з «Червоним капелюхом». (слайд 18)

Які емоції у вас виникли під час дослідницької роботи?

(варіанти відповідей)

• Захоплення.
• Цікавість.
• Задоволення від виконаної роботи.

VІ. Закріплення вивченого матеріалу.

Поки ви працювали, на телефон прийшло декілька повідомлень у Messenger. (слайд 19)

Виконання усних вправ.

1) Чи існує трикутник із сторонами 2 см, 5 см, 7 см? (Ні, бо 7=2+5)

2)Чи існує рівнобедрений трикутник із бічною стороною 9 см і основою 18 см? (Ні, бо 18=9+9)

3) Периметр трикутника 20 см. Чи може одна з його сторін дорівнювати 9 м? (Так, бо на дві інші припаде 11 см, а 9<11)

4) Сторони трикутника 12,18, 8 см. Проти якої  сторони буде  найменший кут? (Проти сторони 8 см).

5)Знайдіть помилку на рисунку 7. (слайд 20)

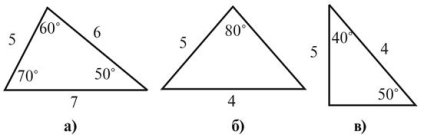
Працюємо з «Білим капелюхом». (слайд 21)

Які властивості трикутника ми використовували, щоб розв’язати ці завдання?

(варіанти відповідей)

- Співвідношення між сторонами і кутами трикутника.

- Нерівність трикутника.

•   Виконання письмових вправ (слайд 22).

Нам знову прийшло повідомлення у додаток «Книги». А це означає, що ми працюємо з книгою, а, зокрема, і нашим підручником.

 

Задача. (біля дошки)

Для оздоблення серветки квадратної форми

досить 140 см мережива. Господиня вирішила

розрізати серветку на два рівні трикутники

і обшити дві трикутні серветки по периметру.

Чи вистачить їй 210 см мережива?

 

 

Розв’язання: Р_кв.=140 см.

140:4=35 (см) – сторона квадрата і трикутника;

210-140=70 (см) – залишиться на 2 сторони BD.

BD>AB, то BD>35, тому 210 см мережива не вистачить.

Відповідь: ні.

Працюємо з «Жовтим капелюхом». (слайд 23)

Де можна використовувати вивчені властивості трикутника?

(варіанти відповідей)

• На будівництві.
• У побуті.
• На уроках трудового навчання.

Робота з підручником : №486. (Коментуємо з місця) (слайд 24)

• АВ=3,3с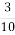м=3 см=3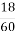 см, ВС=3см=3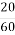см, АС=3 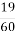см. Найбільша сторона – ВС, отже – найбільший кут А

 

№497

Дві сторони трикутника дорівнюють 2,9 см і 8,3 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?

Розв’язання

 Нехай невідома сторона дорівнює а см. Тоді

<а<2,9+8,3

5,4<а<11,2

а= 11

Відповідь : 11 см.

№499

Чи можуть сторони трикутника бути пропорційними числам:

1)2,3,4

2)7,8,15

3)5,3,7

 

Розв’язання

Нехай  коефіцієнтом пропорційності буде х см.

1)2х+3х>4х

   5х>4х-існує

Оскільки найменша сторона трикутника очевидно менша від суми двох інших сторін, то нерівність трикутника достатньо перевірити для найбільшої сторони.

2)Визначимо найбільшу сторону(15)

  Нехай  коефіцієнтом пропорційності буде х см.

  15х=5х+3х

  15х=15х-сторони не можуть бути пропорційні числам 7,8,15

3) Нехай  коефіцієнтом пропорційності буде х см.

    7х<5х+3х

    7х<8х-трикутник існує.

Працюємо з «Чорним капелюхом». (слайд 25)

Які  труднощі можуть виникнути при розв’язуванні задач на застосування вивчених властивостей?

• Помилки в обчисленнях
• Не вміння застосовувати вивчений матеріал при розв’язуванні поставлених задач

VІІ. Рефлексія. (слайди 26-30)

Поки ми розв’язували задачі на телефон, знову надійшли повідомлення в Instagram. Давайте розшифруємо сканером QR-кодів і прочитаємо їх.

Цікаві факти про трикутник.

1. Трикутники широко застосовуються в нашому житті. Давногрецький мислитель Платон говорив: «Усе в світі складається з трикутників».

2. Бермудський трикутник – район в Атлантичному океані, у якому начебто відбуваються таємничі зникнення морських і повітряних суден.

3. Трикутник також є поширеним символом на писанках. У ньому втілена ідея триєдиності: Неба, Землі, Води. Цей знак також символізує батька, матір, дитину. Це символ божественної Трійці.

4. Лісова пташка малинівка, за свідченням орнітологів, здійснює перельоти тільки вночі. Орієнтується на великий літній трикутник на зоряному небі: Вега, Денеб, Альтаїр.

 

Можна наводити ще багато цікавих фактів про трикутник, але наш урок завершується.

Працюємо з «Зеленим капелюхом». (слайд 31)

Скласти сенкан до слова трикутник.

Зразок:

Кут.

Тупий, суміжний.

Вимірюємо, будуємо, порівнюємо.

Бісектриса ділить кут навпіл.

Фігура.

(варіанти відповідей)

Трикутник.

Рівнобедрений, прямокутний.

Вивчаємо, будуємо, розв’язуємо.

Трикутники широко застосовуються скрізь..

Фігура.

 

VІІІ. Підбиття підсумків уроку.

Працюємо з «Синім капелюхом». (слайд 32)

Давайте повернемося до епіграфу уроку.

У чому повчальність східної приказки і який зв'язок з нашим уроком?

1. Чи цікаво було вам сьогодні на уроці?
2. Чи переконалися ви в тому, що геометрія потрібна і цікава?
3. Що нового ви навчилися сьогодні?
4. Що вам найкраще сподобалося?

ІX. Домашнє завдання.

І отримайте ще повідомлення на Viber. (слайд 33)

 Опрацювати § 18,  

Виконати №№ 490, 498, 505(а)^*.

Додаткове завдання