Урок "Трикутник та його елементи"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

НА ТЕМУ:

«Трикутник та його елементи»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕТА:

 

1. Забезпечити засвоєння нового матеріалу, сформулювати поняття трикутника, його елементів.

2. З метою розвитку інтелектуальних здібностей, сформувати вміння переносити раніше отримані знання та вміння в нову ситуацію.

3. Розвивати в учнів бажання та почуття необхідності у вивченні геометрії, розвивати їх самостійність та творчість.

 

ХІД УРОКУ

 

I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

Учням повідомляється тема та мета уроку.

II. ПІДГОТОВКА ДО ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Ввідне слово вчителя

Серед великої кількості різноманітних геометричних фігур на площині виділяють велике сімейство МНОГОКУТНИКІВ.

Назви геометричних фігур мають цілком визначений зміст.

Придивіться уважніше до слова „многокутник” та скажіть з яких частин складається це слово. Слово „многокутник” вказує на те, що в усіх фігур з цього сімейства „багато кутів”.

Підставте в слово „многокутник” замість частинки „много” конкретне число, наприклад 5.Ви отримаєте П’ЯТИКУТНИК. Або – 6. Тоді – ШЕСТИКУТНИК. Вы получите ПЯТИУГОЛЬНИК. Або 6. Тогда – ШЕСТИУГОЛЬНИК. Замітьте, скільки кутів, стільки ж і сторін. Тому ці фігури цілком можна було б назвати „многосторонником”.

 2. Завдання 1

На малюнку геометричні фігури. Використовуючи малюнок, назвіть ці фігури.

 

 

 

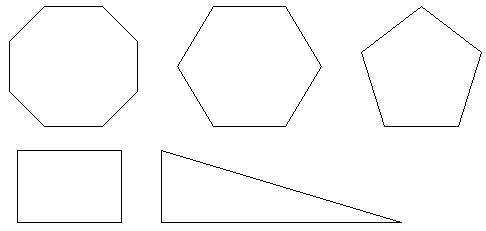
Яким найменшим числом можна замінити „много” в многокутнику?

(Відповідь: 3)

З яким із видів многокутників ми познайомимося на сьогоднішньому уроці ви відповісте мені, відгадав загадку.

ЗАГАДКА:

Жили-были три подружки
В разных домиках своих.
Три веселых хохотушки – 
Точками все звали их.
Между этими домами
Реки длинные текли.
Точки очень не хотели
Ножки промочить свои.
И тогда они решили
Между домиками взять
Сделать мостики большие,
Чтобы в гости прибегать.
Мост с мостом соединился,
Что же, в общем, получился?
(Треугольник).

(На екранах моніторів іде показ даної загадки в вигляді презентації)

 

III. ПОСТАНОВКА ЦІЛЕЙ ТА ЗАДАЧ УРОКА

Сьогодні ми розглянемо першу фігуру із сімейства многокутників – ТРИКУТНИК. Згадаємо його елементи, поняття, пов’язані з даною фігурою та навчимося практично використовувати отримані знання та вміння при розв’язуванні задач.

IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

Запис числа, теми уроку на дошці та в зошитах.

1. Трикутник – найпростіша фігура: три сторони, три вершини і три кута. Математики називають його двохмірним “симплексом” – з латини означає найпростіший. Тому в силу своєї такої простоти трикутник є основою для багатьох вимірів.

Через площу трикутника виражається площа любого многокутника, досить розбити многокутник на трикутники, знайти їх площі та додати їх результати.

Ще 4000 років назад в одному єгипетському папірусі велася мова про площу трикутника.

Через 2000 років в Древній Греції дуже активно велося вивчення властивостей трикутника. Піфагор відкрив свою знамениту формулу.

Особливо дуже активно проводилися дослідження властивостей трикутника в XV-XVI століттях. Великий вклад в цю теорію вніс знаменитий математик Леонард Эйлер.

Імператор Франції Наполеон свій вільний час приділяв заняттям з математики, особливо – вивченню властивостей трикутників. (З книги “Я познаю мир”)

2. Математична перерва

Я дуже люблю трикутники! Тому відразу повідомляю математичну перерву. Перевірте мої твердження та якщо необхідно виправте допущені в них помилки:

Любий трикутник має три сторони.

В жодному трикутнику немає ні одної прямої.

Любий трикутник побудований з трьох відрізків.

Любий трикутник побудований з трьох відрізків, що з’єднують між собою три точки, що не лежать на одній прямій.

Любий трикутник має три кути.

Любий трикутник має три вершини.

(Учні усно відповідають на запитання, поставлені вчителем)

3. Основні елементи трикутника

 

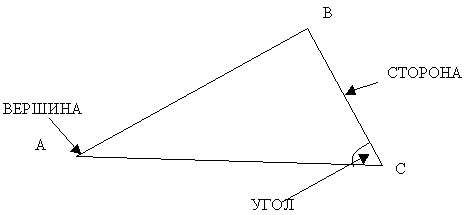
(Після розгляду всіх елементів трикутника дається усне визначення трикутника, зроблене самими учнями. Потім це визначення коректується вчителем та записується учнями в зошити):

ТРИКУТНИК – геометрична фігура, побудована з трьох точок (вершин) та трьох попарно з’єднаних відрізків (сторін).

4. Задача

Земельна ділянка має трикутну форму. Скільки необхідно метрів проволоки, щоб обнести цю ділянку забором?

(Відповідь: виміряти сторони та знайти суму їх довжин.)

Як називається сума довжин всіх сторін трикутника?

(Відповідь: периметр.)

Р_авс = АВ + ВС + СА (ед.)

 

V. ПРАКТИЧНЕ ЗАВДАННЯ

(виконуються завдання № 268 стр.79, № 272, 275 стр.80 по підручнику Геометрия 7, Бевз Г.П., Бевз В.Г., Владимирова Н.Г.)

Намалюйте трикутник та позначте його вершини буквами M, N и P.

а) назвати всі кути та сторони трикутника;

б) за допомогою лінійки виміряйте сторони та знайдіть периметр трикутника.

5. Повернення до трикутника

Три вершини, 3 сторони, 3 кута. Сторона АС лежит напроти кута С ВС лежит напроти кута А СА лежит напроти кута В До сторони АВ прилягають кути А і В До сторони ВС прилягають кути В і С До сторони АС прилягають кути А і С. Кут А знаходиться між сторонами АВ та АС Кут В знаходиться між сторонами АВ та ВС Кут С знаходиться між сторонами АС та ВС.

Серед даних, приведених в таблиці, тверджень визначити їх справедливість.

Накреслити трикутник DEF так, щоб кут E був прямим.

Назвіть:

а) сторони, що лежать напроти кутів: D, E, F;

б) кути, що лежать напроти сторін: DE, EF, FD;

в) кути, що прилягають до сторін: DE, EF, FD.

VI. РОБОТА З ТРИКУТНИКАМИ

Перед вами конверти, в яких лежать трикутники. Серед них ви повинні віднайти два рівних трикутника. Поясніть свою відповідь. (За допомогою накладання).

Щоб трикутники співпали, скільки для цього необхідно елементів?

При суміщенні трикутників попарно співпадуть і їх вершини, сторони та кути. Отже, якщо два трикутники рівні, то елементи одного трикутника будуть відповідно рівними елементам другого трикутника. В рівних трикутниках напроти відповідно рівних сторін лежать рівні кути, і навпаки: напроти відповідно рівних кутів лежать рівні сторони.

 

VII. ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ

Периметр одного трикутника більший периметра другого. Чи можуть бути рівними ці трикутники? Відповідь пояснити.

Задача: трикутники АВС та MNP рівні. Кут А рівний куту М, кут В рівний куту N та кут С рівний куту Р. Знайти сторони трикутника MNP, якщо АВ = 7 см, ВС = 5 см, СА = 3 см.

VIII. ВИСНОВКИ З УРОКУ

Учні відповідають на запитання на стр. 77 підручника.

Оцінювання роботи учнів на уроці та виставлення оцінок.

IX. ДОМАШНЄ ЗАВДАННЯ

§9, № 265, 271, 277(інд.)