Урок геометрії у 7 класі "Властивість бісектриси, медіани і висоти рівнобедреного трикутника"

Тема. Властивість бісектриси, медіани і висоти рівнобедреного трикутника.

Мета:

навчальна: засобами дослідницької діяльності сформулювати і довести властивість бісектриси рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач;

розвивальна: розвивати пізнавальні здібності учнів; формувати вміння бачити закономірності; розвивати просторове уявлення, самостійність мислення, вміння аналізувати відповіді однокласників, доводити власну точку зору.

виховна: виховувати працьовитість, цілеспрямованість; виховувати активну позицію в навчанні, здатність відстоювати   свою думку, готовність до співпраці

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: Креслярські інструменти, мультимедійний проектор, комп’ютер, моделі рівнобедрених трикутників, сигнальні картки для гри «Вірю – не вірю», картки і плакат завданнями.

Підручник: «Геометрія» підручник для 7 класу загальноосвітніх навчальних закладів (О.С.Істер. — Київ : Генеза, 2015. — 184 с. : іл.)

Хід уроку

І. Організаційний етап

    Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

        Щоб налаштуватися на урок і заспокоїтися, проведемо таку вправу. Заплющте очі та подумки уявіть собі рівнобедрений трикутник… рівносторонній… різносторонній… медіану цього трикутника… бісектрису…висоту…

    Роботу на уроці частково будете оцінювати ви самі у картках самооцінювання.

ІІ. Перевірка домашнього завдання

     Що було задано на домашнє завдання?

1. Вивчити тему «Висота, бісектриса і медіана трикутника» (§ 15).
2. Завдання №  353 (відп.: 70°), 354 (відп.: 10 см і 10 см).

На повт.: № 374 (відп.: 9 см, 30 см, 30 см).

3. Виконати вправи на learningapps.org (класифікація трикутників).

ІІІ. Актуалізація опорних знань

1. Термінологічний диктант (усно)

1.Трикутник, у якого тільки дві сторони рівні, називається ....

(Рівнобедреним)

2. Дві рівні сторони рівнобедреного трикутника називають … .

(Бічними)

3. Третя сторона рівнобедреного трикутника називається … . 

(Основою)

4. Трикутник, який не є рівнобедреним, називається … .  

(Різностороннім)

5.Трикутник, у якого всі сторони рівні, називається … .

(Рівностороннім)

6. Кути при основі рівнобедреного трикутника … .

(Рівні)

7. Якщо в трикутнику два кути рівні, то він … .

(Рівнобедрений)

8. Відрізок, що сполучає вершину трикутника з серединою протилежної сторони, називається … .

(Медіаною)

9. Відрізок бісектриси кута трикутника від його вершини до протилежної сторони називається … .

(Бісектрисою трикутника)

10. Перпендикуляр, опущений з вершини трикутника на пряму, на якій лежить протилежна сторона, називається … .

(Висотою трикутника)

11. Скільки перпендикулярів можна провести через дану точку до прямої?

 (Один)

2. Гра «Вірю – не вірю» (за допомогою сервісу Plickers).

1. _ΔPQT – рівнобедрений.                  
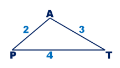
2. FD - висота _ΔEFG     
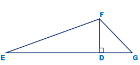
3. PS – бісектриса _ΔRPT   
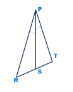
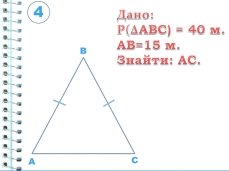
4. P(_ΔKLM) =18см,  KL=10см 
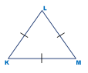
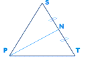
5. PN – висота _ΔSPT
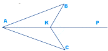
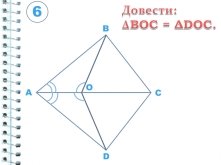
6. _ΔABK=_ΔACK – за ІІ ознакою рівності трикутників
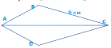
7. DC = 10 см 
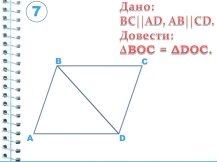
8. Трикутники рівні за І ознакою рівності трикутників 
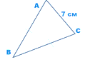
9. P(_ΔABC) = 25 см,  AB = 9 см 
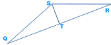
10. S T – медіана _ΔQSR 

 

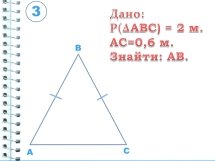3. Фронтальне виконання вправ (усне), індивідуальне (письмово) за готовими кресленнями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ІІІ. повідомлення мети уроку, мотивація навчальної діяльності

Дослідження проблеми (робота в групах)

     Проведемо невелику дослідницьку роботу. Ми знаємо, що в трикутнику можна провести три медіани, три бісектриси та три висоти. Разом – дев’ять різних відрізків. Дослідимо питання: Чи в будь-якому трикутнику можна провести 9 різних відрізків?

1. Троє учнів по черзі дають означення медіани, бісектриси та висоти трикутника, виконують їх побудову у середовищі програми Geogebra та на дошці.
2. (Паралельно 2 групи учнів працюють з макетами рівнобедрених трикутників різних видів) – Вправа  «Геометричне орігамі». 

          Знайдіть на своїй моделі рівнобедреного трикутника однакові на ваш погляд елементи, назвіть їх. Яким чином можна пересвідчитись в їх рівності за допомогою моделі?

1.               Зігніть модель трикутника таким чином, щоб співпали рівні сторони. Які ще елементи виявилися однаковими?
2.               Сформулюйте висновки.

3. (Паралельно) всі інші учні виконують практичну роботу за готовими рисунками. Кожен учень отримує аркуш із зображенням рівнобедреного трикутника та виконує послідовно завдання практичної роботи. Після виконання роботи учні висловлюють свої гіпотези.

         Перевірте, чи є трикутник рівнобедреним. Якщо так, запишіть його основу, бічні сторони.

 Із вершини, протилежної до основи, проведіть послідовно:

1) медіану;

2) бісектрису;

3) висоту.

Що ви помітили? Сформулюйте гіпотезу.

Завдання учням. За допомогою побудованої раніше моделі у середовищі Geogebra з'ясувати, у якому співвідношенні перебувають бісектриса, медіана і висота рівнобедреного трикутника, проведені до основи, у залежності від довжин бічних сторін.

 

 

 

 

 

 

 

 

 

 

 

 

 

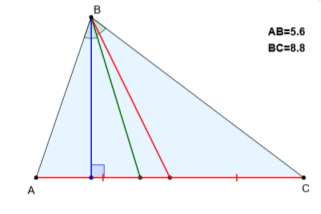
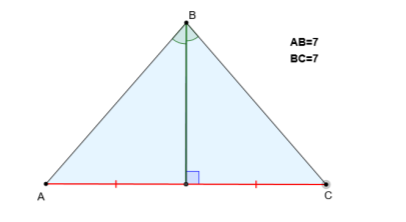
     Отже, завданням уроку є підтвердження або спростування гіпотез учнів, у разі підтвердження засвоєння відповідної властивості медіани, бісектриси і висоти рівнобедреного трикутника та формування вміння розв’язувати задачі на застосування цієї властивості.

ІV. Засвоєння знань

План вивчення нового матеріалу

1. Формулювання теореми про медіану, бісектрису, висоту рівнобедреного трикутника та колективне її доведення.

У рівнобедреному трикутнику бісектриса, проведена до основи, є медіаною і висотою.

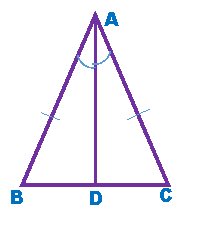 Дано: ∆ АВС, АВ = АС,

АD – бісектриса

                                          Довести:

а) AD – медіана ∆ АВС

б) AD – висота  ∆ АВС

Доведення.

1. Розглянемо ∆ АВD і ∆ АСD:

   1. АВ = АС – за умовою,

   2. ∠ ВAD = ∠ СAD – за властивістю бісектриси,

   3. АD –  спільна сторона.

Звідси, ∆ АВD = ∆ АСD – за першою ознакою рівності трикутників.

ВD = СD, тобто АD – медіана ∆ АВС.

2 . З рівності трикутників випливає,що ∠ ADВ = ∠ ADС, але вони суміжні, тому дорівнюють 90° , тобто АD – висота ∆ АВС.

Отже, ми встановили, що в рівнобедреному трикутнику бісектриса, медіана і висота, проведені до основи, співпадають. Тому можна поміняти формулювання теореми:

Наслідок 1. У рівнобедреному трикутнику медіана, проведена до основи, є бісектрисою і висотою.

Наслідок 2. У рівнобедреному трикутнику висота, проведена до основи, є медіаною і бісектрисою.

 

V. первинне закріплення знань.

Виконання усних вправ

1. Чи правильне твердження: «Бісектриса рівнобедреного трикутника є медіаною і висотою»?
2. У рівнобедреному, але не рівносторонньому трикутнику проведено всі медіани, бісектриси й висоти. Скільки різних відрізків проведено? Як зміниться відповідь, якщо поданий трикутник є рівностороннім?

3. У трикутнику ABC відрізок AD — медіана, бісектриса й висота. Назвіть рівні сторони трикутника.

4. У трикутнику ABC ∠A=∠C. Бісектриса якого з кутів трикутника збігається з медіаною та висотою?

5. У трикутнику MNK

∠M =∠K=40°, ∠N =100°,

NP — медіана. Знайдіть кути ΔMNP.

6. Як у рівнобедреному трикутнику OMK з основою OK провести висоту (бісектрису) з вершини M, використовуючи тільки лінійку з поділками?

 

 

 

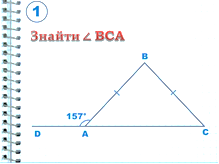
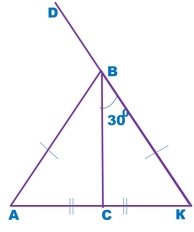7. Знайти кут DBA:

 

 

 

 

 

 

 

 

 

 

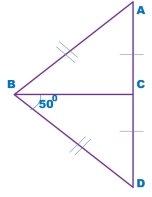
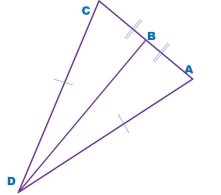
Виконання письмових вправ

1. Побудуйте рівнобедрений трикутник ABC з основою AC і тупим кутом B.

1) Проведіть висоту AD. Чи лежить точка D на відрізку BC?

2) Проведіть медіану BM. Чи є рівними кути ABM і CBM? Чому?

2. У трикутнику ABC ∠A=∠C, BD — бісектриса трикутника. Доведіть, що AD=CD.

3. На висоті MP рівнобедреного трикутника KMN з основою KN позначено точку O (рис. 1). Доведіть, що трикутник KON рівнобедрений.

4. Доведіть, що медіани рівних трикутників, проведені до відповідно рівних сторін, рівні.

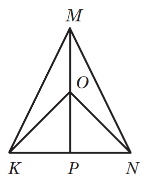
Рис. 1

5. Трикутники ABC і DBC рівні (рис. 2). Доведіть, що точка перетину відрізків AD і BC ділить відрізок AD навпіл.

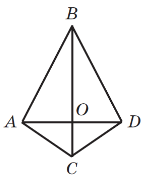
Рис. 2

 

Слово вчителя.

      Для теореми про властивість бісектриси рівнобедреного трикутника справедливою буде й обернена теорема:

1. Якщо бісектриса трикутника є його висотою, то трикутник рівнобедрений. Або:
2. Якщо медіана трикутника є його висотою, то трикутник рівнобедрений. Або:
3. Якщо медіана трикутника є його бісектрисою, то трикутник рівнобедрений.

      Ці твердження можна вважати ознаками рівнобедреного трикутника.

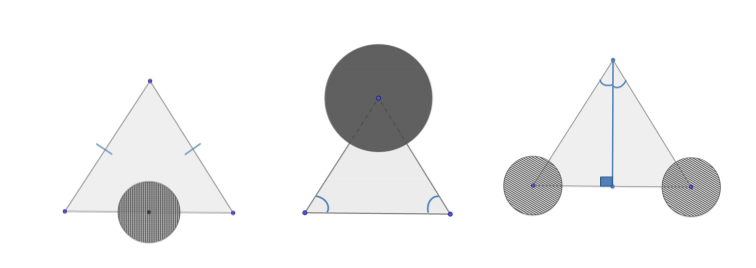
     Яке практичне застосування мають ознаки рівності трикутників? У різноманітних механізмах часто зустрічаються трикутні деталі. Іноді треба встановити, чи є трикутник рівнобедреним, не маючи доступу до його сторін. Яким чином це можна зробити?

Якщо недоступною є одна сторона (слайд 1), то те, що трикутник рівнобедрений легко встановити за означенням.

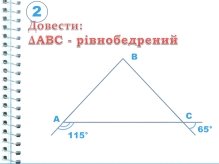
А якщо недоступними є дві сторони та їх спільна вершина, як встановити, чи є рівнобедреним трикутник? (слайд 2). (За ознакою рівнобедреного трикутника за двома кутами).

А якщо недоступними є всі три сторони і два кути, доступною є лише одна з вершин? (Провести висоту, і перевірити, чи не буде ця висота бісектрисою)

 

 

 

 

 

 

 

 

 

 

 

 

 

VІ. Підсумки уроку

Теоретичний тест. (Самоперевірка за слайдом)

1. Медіана в рівнобедреному трикутнику є бісектрисою і висотою. Це твердження:

1. Завжди правильне;
2. Може бути правильним;
3. Завжди неправильне.

2. Якщо трикутник рівносторонній, то:

1. Він рівнобедрений;
2. Всі його кути рівні;
3. Будь-яка його висота є медіаною і бісектрисою;
4. Всі відповіді A,B, C є правильними.

3. В якому трикутнику тільки одна його висота ділить його на два рівні трикутники?

1. В будь-якому;
2. В рівнобедреному;
3. В рівносторонньому.

4. Якщо трикутник рівнобедрений, то:

1. Він рівносторонній;
2. Будь-яка медіана є бісектрисою і висотою;
3. Відповіді A i B неправильні.

5.  В якому трикутнику будь-яка його висота ділить його на два рівні трикутники?

1. В будь-якому;
2. В рівнобедреному;
3. В рівносторонньому.

VІІ. Домашнє завдання

1. Вивчити тему «Властивість бісектриси рівнобедреного трикутника» (§ 15).
2. Розв’язати задачу № 371^*. Довести, що коли медіана рівнобедреного трикутника є його бісектрисою, то трикутник рівнобедрений.
3. Виконати вправи на сайті learningapps.org (вхід за індивідуальними паролями).