Урок геометрії у 8 класі на тему "Застосування подібності трикутників до розв'язування задач"

Тема. Застосування подібності трикутників до розв’язування задач

Цілі: - формування предметних компетентностей:

• формування ключових компетентностей:

• формувати вміння оперувати інформацією, поданою в рисунках, доводити правильність власного судження або визнавати помилковість;
• будувати та досліджувати математичні моделі природних явищ та процесів;
• сприяти усвідомленню взаємозвязку математики та літератури.

Тип уроку: застосування знань і вмінь.

Обладнання і наочність: презентація «Ознаки подібності трикутників»; картки із завданнями за готовими рисунками; портрет А. Конан Дойла; уривок із оповідання (екранізація) «Обряд родини Масгрейвів» А. Конан Дойла; підручник (Істер О. С. Геометрія : підруч. для 8-го кл. загальноосвіт. навч. закл. / О. С. Істер. – Київ : Генеза, 2016).

Епіграф до уроку: «У всьому треба шукати логіку. Де її не вистачає, треба підозрювати обман» (Артур Конан Дойл, «Загадка Торського мосту»).

Хід уроку

І. Організація початку уроку

ІІ. Перевірка домашнього завдання. Актуалізація опорних знань

1. Перевірка завдання за підручником («Метричні співвідношення в колі»).
2. «Німий диктант».

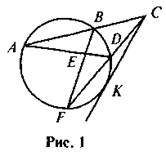На дошці виконане зображення ситуацій, що можуть бути описані метрич­ними співвідношеннями в колі (рис. 1).

Учитель формулює загальне завдання для всіх учнів: для відрізків, на які він буде вказувати, записати пра­вильну рівність (відповідне метричне співвідношення). І далі мовчки вказує по черзі на відрізки хорд, січних, дотичних. По закінченні ви­конання роботи відбувається само- або взаємоперевірка робіт із комен­тарем.

3. Метод «Передбачення».

- Яке завдання ставить кожен з вас собі на уроці?

(Формується спільна мета)

ІІІ. Удосконалення знань і вмінь

Слово вчителя

Мабуть, багато з вас чули про дедуктивний умовивід Шерлока Холмса. Слово «дедукція» (deductio) – латинського походження. Дедуктивне міркування передбачає висновок, зроблений логічним шляхом, від загального до часткового. Індуктивне міркування – навпаки.

Той же Шерлок Холмс, маючи перед очима повну картину злочину, переходив до розгляду окремих деталей: виявляв ймовірних учасників, вивчав їхню поведінку і наявність мотивів. І таким чином визначав злочинця. «Відкиньте всі неможливе, – говорив він, – і те, що залишиться, і буде відповіддю, якою б неймовірною вона не здавалася». Проте насправді Шерлок Холмс вдало переходив від одного методу міркування до іншого.

Давайте  ми сьогодні уявимо себе видатними детективами і спробуємо розплутати одну із загадок Артура Конан Дойла.

Застосування подібності трикутників до проведення вимірювальних робіт на місцевості (за уривком оповідання А. Конан Дойла «Обряд родини Масгрейвів»).

***

«Кому це належить?

Тому, хто пішов.

Кому це належатиме?

Тому, хто прийде.

В якому місяці це було?

В шостому, починаючи з першого.

Де було сонце?

Над дубом.

Де була тінь?

Під берестом.

Скільки треба зробити кроків?

На північ — десять і десять, на схід — п’ять і п’ять, на південь — два і два, на захід — один і один і потім униз.

Що ми віддамо за це?

Все, що маємо.

Заради чого віддамо?

Заради надії».

***

…Всі наведені в ньому відстані стосуються певного місця, на яке натякає цей документ; отже, коли б ми знайшли те місце, то опинились би на шляху до розкриття таємниці, що її давні Масгрейви вважали за необхідне зберегти від забуття в такий дивний спосіб. Для початку ми мали два орієнтири — дуб і берест. Що стосується дуба — тут не могло бути ніяких сумнівів. Просто перед будинком, ліворуч від під’їзної алеї, стояв дуб, справжній патріарх, одне з найвеличніших дерев, яке я будь-коли бачив.

***

Тут у вас є старі берести? — спитав я.

— Отам був один, дуже старий, але десять років тому в нього вдарила блискавка, і ми його спиляли.

***

— Мабуть, зараз уже неможливо встановити, який був берест заввишки? — спитав я.

— А чого ж: шістдесят чотири фути.

— Як ви це вирахували? — здивувався я.

— Коли мій старий домашній учитель давав мені задачі з тригонометрії, вони завжди були побудовані на вимірюванні висоти. Через це я ще хлопцем вирахував висоту кожного дерева й будівлі в нашому маєтку.

***

Я пройшов разом з Масгрейвом до його кабінету й вистругав собі цей ось кілочок, до якого прив’язав довгу мотузку з вузликами, що позначали кожен ярд. Потім я зв’язав два вудлища — це дало мені шість футів,— і повернувся зі своїм клієнтом до того місця, де колись ріс берест. Сонце саме торкнулося верхівки дуба. Я закріпив вудлище вертикально, визначив напрямок тіні і виміряв її. Вона була дев’яти футів завдовжки.

Я взявся розраховувати далі.

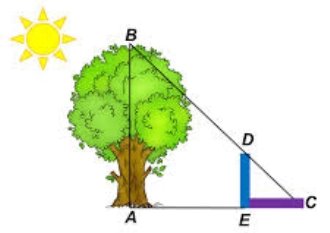
Запропонувати учням побудувати математичну модель цієї прикладної задачі; довести подібність трикутників АВС і EDC і знайти шукану тінь дерева.

***

Якщо вудлище в шість футів завдовжки дає тінь в дев’ять футів, то дерево заввишки шістдесят чотири фути кидало б тінь довжиною в дев’яносто шість футів…

IV. Розв'язування задач

Робота в парах

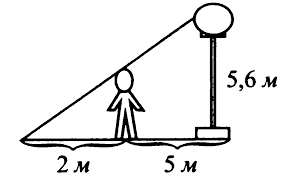
1. Довжина тіні дерева 21 м. В ту ж саму годину доби тінь людини зростом 180 см становить 2,7 м. Яка висота дерева?

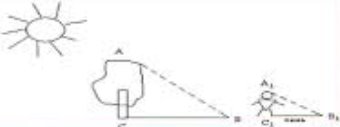
2. Знайдіть зріст людини за даними на малюнку:

V. Домашнє завдання

1. Завдання за підручником.

2. Практичне завдання.

Знайдіть висоту дерева, що росте біля вашого будинку, користуючись властивостями подібності.

Проведіть необхідні вимірювання в сонячну погоду в різний час (в першій половині дня, опівдні, надвечір).

Запишіть у зошиті результати вимірювань. Виконайте необхідні обчислення. До якого висновку ви прийшли? Запишіть його.

VI. Підбиття підсумків уроку. Рефлексія

 Незакінчені речення.

На уроці я:

- дізнався...

- зрозумів...

- навчився...

- найбільший мій успіх - це...

- найбільші труднощі я відчув...

- я не вмів, а тепер умію...

- я змінив своє ставлення до...

- на наступному уроці я хочу...