Урок геометрії в 9 класі. Урок однієї задачі.

Урок геометрії в 9 класі

Тема уроку: Урок однієї задачі.

Мета уроку: формувати в учнів вміння застосовувати свої теоретичні знання в практичній діяльності. Вчити їх, як одну й туж саму проблему можна вирішувати різними способами. Зокрема, як можна розв’язати задачу про  трапецію аналітичним, координатним та векторним способами.

Тип уроку: комбінований.

Задача. Довести, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів бічних сторін, плюс подвоєний добуток основ.

Заздалегідь, на останньому уроці, розбиваємо клас на 4 групи по бажанню учнів. Самі учні визначають капітана, який потім розподіляє обов’язки між членами групи.

Формулюємо задачу. Вказуємо кожній групі, яким способом повинна розв’язуватись задача (аналітичним, координатним та векторним).

Хід уроку

Урок починається з того, що представники кожної групи виходить до дошок і відтворюють свій спосіб розв’язування, І і ІІ група розв’язують задачу аналітичним способом, ІІІ група – координатним, а IV – векторним.

Поки четвірка учнів працює, решті учням класу пропоную задачу і спосіб розв’язання.

Задача. Сторона ромба дорівнює 1, а сума діагоналей  дорівнює 4. Знайти площу ромба.

Розв’язання

Нехай діагональ ромба будуть

, а 16.

Звідси ;

або

 

Маємо ( а – сторона ромба) S=4-1=3 (кв. од.)

Запитуємо учнів, чи згідні вони з таким незвичним розв’язанням? Учні погоджуються. Далі пропоную їм розв’язати задачу іншим способом, поставивши спочатку кілька навідних питань. Швидко зорієнтувавшись один з учнів представляє свій розв’язок.

Нехай одна з діагоналей , тоді діагональ . З , за т. Піфагора .

. Це рівняння не має коренів, а тому задача розв’язку не має.

Одержали суперечність. Де ж тоді вірне розв’язання? Де ховається помилка?

Підводим учнів до того, що помилку допущено у першому випадку.

(ВС=1).

Нерівність трикутника виконується. Проте, чи буде цей трикутник прямокутний Цей трикутник не прямокутний, оскільки не існує такого х, щоб виконувалася рівність , тобто для цього трикутника не виконується теорема, обернена до теореми Піфагора.

Потім капітани кожної групи представляють коментуючи свої розв’язки.

І спосіб (аналітичний).

Введемо позначення.

 

За теоремою косинусів:

 

        (1)

 

        (2)

     (3)  

       (4)

Додамо всі 4 рівності:

 

Маємо

Нарешті:

ІІ спосіб (аналітичний)

Позначення введені аналогічні попереднім.

Нехай AM=x, a ND = y.

.

  

   (1)

   (2)

Додамо рівності (1) і (2):

Маємо:  .

ІІІ спосіб (метод координат)

Введемо систему координат, як показано на малюнку, а решта позначень аналогічні попереднім.

 

 

 

Нехай

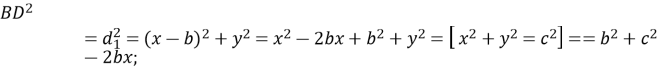
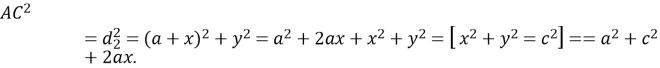
Додамо дві останні рівності:

.

Нарешті:

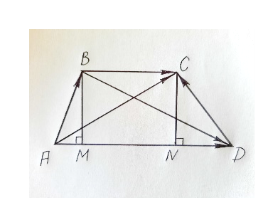ІV спосіб (векторний метод)

Введемо вектори як показано на малюнку.

 

 

 

 

1.                  

    (1)

2.                  

           

    (2)

3.                  

 

    (3)

4.                  

 

   (4)

 

Додамо ці 4 рівності:

 

2

  

Підставимо і одержимо

Нарешті:

Підсумки уроку.

Бачимо, що різними способами можна досягати поставленої мети.

Ви у своїй роботі обираєте найбільш економний, простий спосіб, але не забувайте, що існують і багато інших способів, які в іншій ситуації принесуть вам бажаний результат.