Урок "Геометрична прогресія та її властивості"

АЛГЕБРА,  9 КЛАС

      Тема: Геометрична прогресія та її властивості.

       Мета: ознайомити учнів з поняттями „ геометрична прогресія “,

 „знаменник геометричної прогресії“; розглянути рекурентну                                                                          формулу геометричної прогресії;   властивості геометричної прогресії  та навчити   учнів застосовувати  їх до розв’язування вправ і  задач;

                      розвивати творче і логічне мислення учнів, їх просторову  уяву;

                     виховувати культуру математичних записів.

     Тип уроку: урок засвоєння нових знань.

     Обладнання: засоби мультимедіа.

         Хід уроку

І. Організаційний момент

    Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

ІІ. Перевірка домашнього завдання

    Актуалізація опорних знань учнів. Додаток 4.

       Вправа «Мозковий штурм». Виконуємо вправу за посиланням.

https://learningapps.org/display?v=phoimkvjt22 

1. Послідовність, кожний член якої починаючи, з другого, дорівнює попередньому члену, якого додають одне й те саме число, називають...
2. Як називається це число?
3. Записати формулу n-го члена арифметичної прогресії.
4. Записати  формулу суми  n перших членів арифметичної прогресії.
5.  Скільки членів містить скінченна арифметична прогресія 3,6,9,...,273?
6.  Записати формулу n-го члена арифметичної прогресії 3,6,9,...,273?
7.  Знайти суму чисел 3+6+9+...+273, якщо її доданки є послідовними членами арифметичної прогресії.

          Відповіді на математичний диктант проектуються на екран за допомогою засобів мультимедіа.

           Відповіді на математичний диктант

1. Арифметичною прогресією.

2. Знаменником арифметичної прогресії.

3. a_n=a₁+d(n-1).

4. S_n  =· n

5. 91.

6. a_n=3n.

7. 12558.

ІІІ. Пояснення нового матеріалу 

  1.Означення геометричної прогресії

Випишемо декілька членів послідовності (в_n ), якщо

          b₁=3, b_n+1=2·b_n , nє N.                     

    3,6,12,24,48,96,192,... .

     Кожен член цієї послідовності, починаючи з другого, дорівнює попередньому члену, помноженому на 2.

     Геометричною прогресією називається послідовність ,кожний член якої , починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для послідовності число q називається знаменником геометричної прогресії.

     Перший член   в₁     і знаменник  q  геометричної прогресії можуть бути будь-якими числами, відмінними від 0.

     Іншими словами , геометрична прогресія – це послідовність, яку можна задати такою рекурентною формулою:          b₁=b, b_n+1=b_n·q  ,nє N,                     

 в ≠ 0, q ≠ 0- задані числа.

        Наприклад, 

     4,12,36,108,324,...(в₁ =4, q=3);

     1,-5,25,-125,625,...(в₁  =1, q=-5);

     8,8,8,8,8,8...( в₁  = 8, q=1)

     Отже, щоб задати геометричну прогресію ,досить вказати її перший член і знаменник.

     Зауваження. Кожну арифметичну прогресію з різницею 1 можна також вважати геометричною прогресією зі знаменником 1.

     Отже , рекурентна формула геометричної прогресії

                         b_n+1=b_n· q ,nє N,                     

            де b_n – n-член, q - знаменник геометричної прогресії.

     Приклади геометричної прогресії з життя - розмноження колорадського жука, поширення віруса ГРВІ, з біології – розмноження інфузорії туфельки.

       2. Властивості геометричної прогресії

           1.ТЕОРЕМА 1. Квадрат кожного числа геометричної прогресії, починаючи з другого, дорівнює добутку двох сусідніх його членів:

                                       b_n² =   b_n-1 ·b_{n+ 1}, n  > 1  

                                            Доведення

      За означенням,    b_n-1=  (1), а  b_n+1=b_n· q (2).   

  Перемножимо почленно рівності (1) і (2). Матимемо,

       b_n-1 ·b_n+1=· b_n· q=b_n ².

                                                       Теорему доведено.

  Справедлива і теорема, обернена до доведеної.

            2.ТЕОРЕМА 2. Якщо в послідовності члени не дорівнюють 0 і квадрат кожного члена, починаючи з другого, дорівнює добутку двох сусідніх з ним членів, то така послідовність - геометрична прогресія. 

                                                 Доведення

      Дійсно, якщо послідовність b₁,b₂,…,b_n задовольняє умові   b_n² =   b_n-1 ·b_n+1,                

        n  > 1, то                                                             

                                               = .      

     Оскільки частка від ділення кожного члена послідовності на попередній йому член – одне й те саме число, то ця послідовність – геометрична прогресія.

                                                      Теорему доведено.

          Для будь-якої прогресії з додатними членами доведені теореми можна сформулювати у вигляді такого твердження:

     Кожний член геометричної прогресії, починаючи з другого, дорівнює середньому геометричному двох сусідніх з ним членів ,тобто

                                       b_п =    , n  > 1 .             

        Якщо кожний член числової послідовності з додатними членами, починаючи з другого, дорівнює середньому геометричному сусідніх з ним членів, то така послідовність є геометричною прогресією.

Наприклад. Знайти невідоме число, 3 дані числа є членами геометричної прогресії:   , х , 27.

                    х²= · 27, х²=9, х=3.

     Сформульовані твердження є властивостями геометричної прогресії та пояснюють її назву.

     Після пояснення нового матеріалу  учні записують основні формули в зошити.                           

ІV. Засвоєння нових знань ( виконання вправ).

      Вправа  «Навчаючи – учись». Усні вправи. Додаток 5.

     Робота в зошитах і біля дошки.

1. Написати п’ять перших членів геометричної прогресії, в якій :b₁=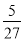, q=3.

Дано: (b_п)- геометрична прогресія.

                 b₁=, q=3.

   Знайти: b₂, b₃, b₄, b₅.

                            Розв’язання

b₂=в₁· q,         b₂= · 3= ;      

 b₃=в₂· q,         b₃= · 3= =;                        

b₄=b₃· q,         b₄= · 3= · 3=5;                            

b₅=b₄· q,         b₅= 5· 3=15.                                 

Відповідь:   b₂= ;  b₃=; b₄= 5; b₅= 15.                                                       

2. Знайти знаменник і п’ятий член геометричної прогресії.

Дано: (b_п ) - геометрична прогресія.

                 b₁=4, bв₂= -2,…

   Знайти: b₅, q.

                            Розв’язання

 q=b₂: b₁,         q= -=- ;                             

     b₃=b₂· q,         b₃=- · (-2)=1;                             

b₄=b₃· q,         b₄= 1· ( - )=-;                 

b₅=b₄· q,         b₅  = - · ( - ) = .                             

Відповідь:   b₅= , q = - .    

Робота із підручником № 767, 769, 771, 773.                                                 

     V. Підсумки уроку та оцінювання учнів.

    Фронтальне опитування учнів по таким контрольним питанням:

       1. Яка послідовність називається геометричною прогресією? Навести приклади з життя.

       2. Сформулювати властивості геометричної прогресії.   

Оцінення учнів.              

VІ. Домашнє завдання.

  Вивчити § 18, № 770, 772, 774.