Урок "Геометрична прогресія та її властивості. Формула n-го члена геометричної прогресії".

Геометрична прогресія та її властивості. Формула n-го члена геометричної прогресії.

Тема. Геометрична прогресія та її властивості. Формула n-го члена геометричної прогресії.

Мета уроку: сприяти засвоєнню учнями поняття  геометричної прогресії, знаменника, основних властивостей та формули n-го члена геометричної прогресі);

виробити вміння  виділяти геометричну прогресію серед інших числових послідовностей, знаходити знаменник та перші кілька членів геометричної прогресії, розв’язувати завдання, що передбачають використання рекурентної формули, формули n-го члена геометричної прогресії та її властивостей.

Формування ключових компетентностей:

уміння вчитися впродовж життя —   сприяти підвищенню інтересу до математики, активності, вміння співставляти та аналізувати, навчатися та оперувати знаннями;

соціальна - здатність працювати в групі, вміння спілкуватися, аргументовано відстоювати свої міркування, висловлювати свою думку.

Тип уроку: засвоєння знань, вироблення вмінь та навичок.

Наочність та обладнання: підручник, картка самооцінювання, картка рефлексії, комп’ютерна презентація.

Хід уроку

I. Організаційний етап

Вчитель перевіряє готовність учнів до уроку, налаштовує їх працювати.

ІІ. Перевірка домашнього завдання

Домашнім завданням було переглянути і опрацювати відео за посиланням https://www.youtube.com/watch?v=E8Xo-teQTLk або створену вчителем презентацію (додаток 3). Продумати і записати запитання, які можуть виникнути після перегляду цього контенту.

Для з'ясування рівня засвоєння учнями змісту і поняття домашнього завдання вчитель пропонує їм виконати тести на платформі “Мій клас”  (див. нижче) з подальшою перевіркою та обговоренням результатів їх виконання, під час яких розглядається зміст основних понять.

Завдання тесту:

1. Наступний член геометричної прогресії −7;21;... дорівнює…
2. Дано геометричну прогресію: −3;9;....

Обчисліть третій член прогресії:

3. Обчисли наступні 3 члени геометричної прогресії, якщо b1 = 7 і знаменник дорівнює 4.
4. Обчисли наступні два члени геометричної прогресії, якщо b1 = 6 і b2= 18.
5. У геометричній прогресії 9; 4,5; ...

5-й член дорівнює

(Число з великою кількістю розрядних одиниць округлюйте до тисячних)

6. Дано геометричну прогресію: −9;45;....

Обчисли знаменник і третій член прогресії.

7. Чотири числа утворюють геометричну прогресію. Якщо до них додати відповідно 2, 5, 7 і 7, тоді отримаємо чотири числа, які утворюють арифметичну прогресію. Обчисли числа, що утворюють геометричну прогресію.

Функція інтернет-ресурсу «Мій клас» дозволяє вчителю бачити  у процесі розв’язування учнями завдань  правильність їх виконання  у кожного школяра і відсоток правильно виконаного кожного завдання. Це дає змогу  відразу виявити рівень засвоєння учнями матеріалу вдома і провести обговорення незрозумілих питань.  Разом з тим учитель відповідає на запитання, які у них виникли під час опрацювання домашнього завдання або створює дискусійне коло між усіма учасниками.

Основна мета уроку формулюється після виконання роботи з урахуванням її результатів. Якщо, є велика кількість помилок та низький рівень виконання роботи, то проводиться закріплення знань та умінь, здобутих вдома; якщо результати виконання роботи задовільні, то акцент переміщується на вдосконалення знань та вміння застосовувати їх у нестандартних ситуаціях.

III. Актуалізація опорних знань

1. Як знайти знаменник геометричної прогресії, якщо відомі її перший та другий члени?
2. Як знайти третій член геометричної прогресії, якщо відомі її перший та другий члени?
3. Як знайти шостий член геометричної прогресії, якщо відомий перший член і знаменник?
4. Відомо, що числа 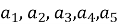утворюють геометричну прогресію із знаменником b. Чи буде геометричною прогресією послідовність:

1)

2)

Чому дорівнює знаменник кожної з цих прогресій?

IV. Відпрацювання вмінь

Зміст письмових вправ уроку залежить від рівня засвоєння знань учнями вдома і випливає з результату виконаних тестів у «Мій клас». І може бути таким:

1) завдання на пряме застосування формули n-го члена геометричної прогресії, у якої заданий перший член і знаменник або задано перелік перших кількох своїх членів;

2)  знайти номер деякого члена геометричної прогресії або перевірити, чи є дане число членом цієї геометричної прогресії;

3) на застосування властивостей геометричної прогресії;

4) прикладні задачі на застосування означення геометричної прогресії і формулу її n-го члена.

Методичний коментар

На цьому уроці слід звернути увагу учнів на словосполучення «починаючи з другого», і на знаменник, він є  постійним для даної геометричної прогресії і  може бути будь-яким (додатним або від’ємним, цілим або дробовим; але не може, на відміну від різниці арифметичної прогресії, дорівнювати 0; це бажано проілюструвати прикладами).

Для вирішення багатьох прикладних завдань важливими є властивості геометричної прогресії, зокрема характеристична властивість,  властивість членів  геометричної прогресії, рівновіддалених від її крайніх членів. Тому, якщо дозволяють особливості класу, можна запропонувати всі ці властивості геометричної прогресії розглянути як додатковий матеріал.

Робота в класі. Для  засвоєння матеріалу на уроці вчитель створює перехресні групи учнів. Кожній групі  присвоюється номер і дається  завдання під тим самим номером (додаток 4). Далі учні виконують компетентнісно орієнтовані завдання, працюють в групах по 4-6 учнів з використанням методу перехресних груп. Учні в групах розраховуються, наприклад на 1-4. Створюються групи нового складу: в одну із них об’єднуються учасники під номером 1, в другу під номером 2 і т.д. Формуються групи згідно номерів. Групам нового складу пропонується розв’язати  по одній задачі . Робота в групах триває близько 6 хвилин. Учні обговорюють розв’язання, записують його в зошит і повертаються у свою групу, повідомляють результати роботи в групі другого складу, коментують способи розв’язання своїх задач. Робота проходить протягом 10-15 хвилин. Учитель в цей момент виконує роль координатора і консультанта, забезпечуючи продуктивну групову комунікацію, надає допомогу учням.

 V. Підсумок уроку

1) Рефлексія

2) Самооцінювання

VIII. Домашнє завдання

1. Опрацювати §19 підручника, відповісти на запитання  (Алгебра: підруч. для 9-го кл. загальноосвіт. навч. закл./ О.С. Істер. – Київ: Генеза, 2017. – 264 с.). Опрацювати відео, підготувати запитання https://www.youtube.com/ watch?v=OA1GeAVRbkc