Урок "Геометричні перетворення"

Тема  уроку:   «Геометричні  перетворення»

Мета: Узагальнити та систематизувати знання учнів з теми: «Геометричні перетворення на площині», удосконалити набуті вміння  і навички про види перетворень при розв’язуванні  задач,  закріпити  практичні навички знаходження симетричних точок та фігур на площині, показати важливість математики у повсякденному житті;

 розвивати пізнавальний інтерес, пам’ять, увагу, образно-геометричне мислення, інтелектуальні та творчі здібності учнів; вміння спостерігати, узагальнювати, робити висновки;

      виховувати культуру математичного мовлення, почуття відповідальності, взаємодопомоги, комунікативні навички, почуття патріотизму, розширювати знання про культурну спадщину народу.
Тип уроку: урок узагальнення і систематизації знань, умінь, навичок.

 Наочність і обладнання: кольорова крейда, виставка фігур із зображеною симетрією, вишиванки і вишиті рушники,  ноутбук, проектор. презентація, конспект  уроку, сигнальні  картки.

Епіграф:Математика  не  лише  вчить  мислити,а й уселяє  віру в безмежні  сили  людського  розуму. Вона  виховує  волю і характер.    (В.Сухомлинський)

                                                  Хід уроку

І. Організаційний  момент.  

Хвилинка налаштування (перевірка готовності учнів до уроку,  налаштування  на роботу).

ІІ. Перевірка домашнього завдання.

Вправа «Відчуй себе вчителем» (самоперевірка) (слайди 3-4 )

  Знайти помилки допущені при виконанні домашнього завдання.

Паралельне перенесення задається формулами  х₁ = х + 3,  у₁ = у + 1. В які точки при цьому паралельному переносі перейдуть точки А(-1;2);  В(-2;4); С(-1;3); Д(-8;-4)?

                                          Розв’язання .

А(-1;2);   х=-1;   у=2,   тоді   х₁ =-1+3=2;    у₁ =2+1=3,

       Правильні відповіді:

А(-1;2) → А₁ (2;3),   В(-2;4)  → В₁ (1;5),     С(-1;3)  → С₁(2; 4),    Д(-8;-4) → Д₁(-5; -3).

2.№707(1) Площі двох квадратів відносяться як 1:4.Знайдіть периметр другого квадрата, якщо периметр  першого дорівнює 8 см^. .

А      В   А₁                   В₁   Дано: АВCD,A₁B₁C₁D₁ – квадрати,                  ; Р _ABCD =8см^..

      

Д       С                                          Знайти: Р         _.

           

             Д₁                      С₁   Розв’язання.

АВCD ~A₁B₁C₁D_{1,                                                               ,} тому

 

 

 

 Р               = 8 · 2 = 16(см).

 Відповідь: 16 см.

ІІІ. Повідомлення теми і мети. (слайд 5) Асоціації на дошці (вишиванки. предмети побуту і ін.)

Вступне слово вчителя.

Ідея перетворень є однією з провідних ідей сучасної математики. За її допомогою з успіхом доводять складні твердження з різних розділів геометрії, які виходять далеко за межі шкільного курсу. За допомогою геометричних перетворень і комп’ютерної  графіки кінематографісти бентежать уяву глядача дивовижними образами і незвичайними перевтіленнями на екрані. Перетворення допомагають художникам правильно будувати композиції картин.   

Симетрія в житті (слайд6-8)

 «Жодна інша наука не навчає так ясно розуміти гармонію природи, як математика»   П.Карус       (слайд 9)

На цьому уроці ми  ще раз розглянемо основні види геометричних перетворень на площині.

Історична довідка. (слайди 10-14 )

    Теорія геометричних перетворень виникла у зв’язку з пізнанням законів зображення предметів на площині. Спроби правильно відобразити на плоскому рисунку природні форми предметів здійснювалися задовго до виникнення писемності – люди малювали на стінах печер, скелях, посуді різноманітні рослини, тварин тощо. Тривала практика підказувала митцям, як передати на рисунку зображуваний предмет - так зароджувалося вчення про відповідності й перетворення. Раніше за інші були встановлені й вивчені закони перспективи. Стародавні греки дотримувалися їх уже в V-IVст.до н.е.

   В Епоху Відродження з’явилися перші фундаментальні дослідження з теорії перспективи, зокрема роботи видатних художників Леонардо да Вінчі (1452-1519) і Альбрехта Дюрера (1471-1528). Розробником математичних основ теорії проективних перетворень(теорії перспективи) став французький інженер і архітектор Жерар Дезарг (1593-1662). (слайди з портретами)

 

 

Жерар Дезарг

 

           

   

Альбрехт  Дюрер          Леонардо да Вінчі         Мішель Шаль            Гаспар Монж

Завдяки теорії перспективи вдалося досягнути достатньої наочності зображень, однак технічний прогрес вимагав точного відтворення об’єктів із дотриманням розмірів. Багато талановитих учених доклали зусиль до створення теорії взаємно однозначних відповідностей на площині й у просторі. Серед них був, зокрема, французький математик Мішель Шаль (1793- 1880), який довів фундаментальну теорему про геометричні перетворення,нині відому як теорема Шаля (Будь-яке зображення зберігає орієнтацію, рух на площині являє собою або  поворот  (зокрема,  центральну  симетрію ),  або паралельне перенесення . Будь-яке змінює орієнтацію рух на площині є осьової або ковзної симетрією) .Підсумував наукові пошуки в галузі геометричних перетворень французький геометр Гаспар Монж (1746-1818), створивши новий розділ геометрії - нарисну геометрію.  Здобутки вчених у вивченні перетворень склали математичну основу розвитку багатьох галузей сучасної техніки.

 

IV.Актуалізація опорних знань.

«Хвилинка повторення»

1.Які види геометричних перетворень вам відомі? (слайд 16 )

 

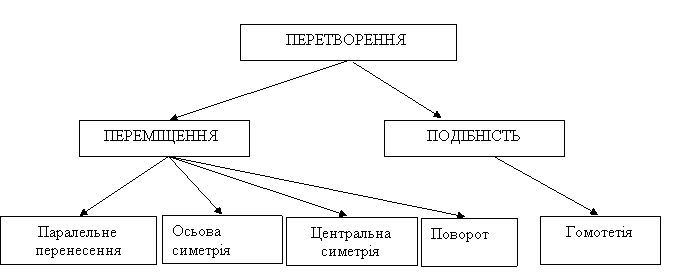
2.Визначте за малюнком вид переміщення . (слайди 17-18)

3. Теоретично-наочний тест.

Вправа «Так чи ні?» Тихе опитування  (робота з сигнальними картками:   тихе опитування:сигнальні картки червона – ні, зелена – так)  (слайд 19)

• Чи правильно, що переміщення переводить відрізок у відрізок?  так
• Чи правильно, що переміщенні коло переходить у коло з тим самим радіусом?   так
• Чи правильно, що при  переміщенні будь-яка пряма переходить у пряму, що їй паралельна?   ні    
• Чи правильно, що перетворення фігури, внаслідок якого зберігаються відстані між точками фігури називається переміщенням?  так
• Чи правильно, що кути між променями при переміщенні збільшуються?ні   - Чи є фігури, які зовсім не мають осей симетрії? Так

     V. Застосуванння вмінь і навичок.

Усні вправи  (слайди 20-22)

1.Знайдіть координати точки, симетричної точці А (-3;1) відносно

а) початку координат;       А' (3;-1)

б) осі абсцис;    А' (-3;-1)

с) осі ординат.   А' ( 3;1)

2. Чи існує паралельне  перенесення,  при якому точка  А (1;3) переходить у точку В(0;2), а точка Д(2;2) переходить у точку С(1;1)? Відповідь: так,  х₁ = х - 1,  у₁ = у -1.

3.Укажіть  точку, в яку при повороті навколо точки О (початок координат) на 90° проти годинникової стрілки переходить точка А (3;2) . Відповідь: А' (-2;3).       4.Встанови відповідність. На виконання 1хв.  (слайд 23)

1		А	центр кола (х+2)2+(у-3)2=9
2	О(-2;3)	Б	х2+у2=4
3		В	гомотетія
4		Г	симетрія відносно точки
5		Д	поворот
6		Е	симетрія відносно прямої

 

1-Б, 2-А, 3-Е, 4-Д, 5-В, 6-Г    (перевірка сигнальними картками) (слайд 24)

 

 

Розв'язування задач (письмово). 

1.(слайд 25). Точки А і С симетричні відносно точки P.  А (-3;5), Р(1;-3). Знайдіть координати точки С.  Відповідь: С(5;-11).

 2.  (слайд 26)Запишіть рівняння кола, у яке переходить коло (x – 3)² + (у – 4)² = 1 при   паралельному перенесенні, при якому точка А(1; 2),переходить у точку В(0; 3).

3.  Вправа «художники». (слайд 27)   

Побудувати трикутник АВС: А(-3;2),   В(-1;6),    С(-8;4)  і симетричний йому

•  відносно осі ОХ;
•  відносно осі ОУ.

    Хвилинка відпочинку (слайд 28)

Які літери є зайві і чому?

А  П  О  Д  Ж  Щ  Е  Ш 

Н  Х  К  У  М  Ф  С Є

Відповідь. Зайвими є літери Щ та У, оскільки ці фігури не мають осі симетрії на відміну від усіх інших фігур.

Розв'язування задач письмово  (перетворення подібності)

1.  №708(1) з підручника (слайд 29).

2.  Знайдіть рівняння кола, у яке переходить коло х²+у²=4 при гомотетії з центром О і коефіцієнтом 2. (слайд 30)

Розв’язання:

При гомотетії з центром О і коефіцієнтом 2 радіус кола збільшується вдвічі, тому R₁=2=4, отже, х²+у²=16 – рівняння шуканого кола. Відповідь: х²+у²=16.

Робота в групах

Дослідити, яке перетворення ми одержимо, виконавши композицію наступних перетворень. Виконати малюнки і зробити висновок.

Перша група

Композиція двох осьових симетрій, осі яких паралельні.

Друга група

Композиція двох центральних симетрій з різними центрами симетрії.

Третя група

Композиція двох паралельних перенесень.

Четверта група

Композиція двох осьових симетрій відносно перпендикулярних осей?

Висновки

1.Композиція двох осьових симетрій, осі яких паралельні є паралельне перенесення.

2.Композиція двох центральних симетрій з різними центрами симетрії є паралельним перенесенням.

3.Композиція двох паралельних перенесень є паралельне перенесення.

4. Композиція двох осьових симетрій відносно перпендикулярних осей є симетрією відносно точки перетину цих прямих.

 

VI. Підбиття підсумків уроку і  оцінювання  учнів.

 

1.Тестові завдання  (слайд 31)

1). Яка фігура має вісь симетрії

А. коло

Б. паралелограм

В. довільний трикутник

Г. прямокутна трапеція

2). Дано точку А(-5;3). Знайти координати точки симетричної точці А відносно початку координат.

А. (2;3)

Б) (5; -3)

В. ( -2;-3)

Г) (0; -3)

3). Паралельне перенесення задано формулами  х' = х - 1,  у '= у + 2.Знайти В', якщо В(1;-1)?

А. (-5;3)

Б. (0;1)

В. (3;3)

Г. (5;-3)

4). Знайдіть точку, симетричну точці (-2;8) відносно осі абсцис.

А. (-2;-8)

Б. (2; -8)

В. (2;3)

Г. (3;-2)

(Після виконання тестових завдань учні обмінюються відповідями і виконують взаємоперевірку)

Відповіді: А Б Б А (слайд 32)

2.Оцінювання учнів

Геометричні перетворення оточують нас у повсякденному житті, вони спостерігаються у будові тіла людини, тварин, рослин і квітів, молекул ДНК, симетричні будівлі ваблять око, симетричне розташування елементів побуту приносить гармонію у наше світосприйняття. Отже вивчення властивостей геометричних перетворень в просторі є важливим і актуальним.

 

VІІ. Домашнє завдання. (слайд 33)

     1). Повторити §§ 17-21

2).Розв'язати задачу:  

Запишіть рівняння прямої, у яку переходить пряма 2х – 3у = 6 при паралельному перенесенні, при якому точка А(-1; 1) переходить у точку В(1; -1).

3). Створити презентацію «Перетворення в архітектурі та будівництві».

Хочу побажати Вам  успіхів у майбутньому і  у вивчені геометрії

Дякую усім за урок!

 

      Додаткові задачі.

1. Гіпотенуза і катет прямокутного трикутника відповідно дорівнюють 5 см і 3 см. Знайдіть довжину найбільшої сторони подібного йому трикутника, площа якого дорівнює 54 см² .
2. Знайдіть рівняння кола, у яке переходить коло (х – 1)² + (y – 2)² = 1 при  гомотетії  з центром О (початок координат), якщо відомо, що точка А(-1; 2) переходить у точку В(-2;4) при цій гомотетії.
3. Знайдіть рівняння фігури, у яку переходить фігура х² + 2х + у² – 2у – 2 = 0 при її повороті навколо початку координат на кут 90° за годинниковою стрілкою.
4. Знайдіть площу ромба з периметром 20 см, якщо він подібний ромбу з діагоналями 30 см і 40 см.
5. Унаслідок гомотетії  з центром   (2; -1) точка А (8; 7) переходить у точку А'. Знайдіть коефіцієнт гомотетії, якщо А'(5;3)?
6. Відповідні сторони двох подібних прямокутників відноситься як 3:5.Знайдть площу більшого прямокутника, якщо площа меншого дорівнює 36см^2.На сторонах АВ і АС трикутника АВС побудовані правильні трикутники АВМ і АСН. Довести, що відстань між точками М і Н дорівнює стороні ВС.