Урок геометрии по теме "Теорема Пифагора"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Цели урока: 

•                 Образовательные – продолжать формировать умения и навыки решать задачи, используя теорему Пифагора; 
•                 Развивающие – развивать навыки самостоятельной деятельности учащихся и навыки само- и взаимоконтроля; прививать ученикам интерес к математике, активизировать познавательную деятельность учеников; 
•                 Воспитательные – воспитывать внимательность, сосредоточенность, культуру математической речи, аккуратность выполнения чертежей. 

Тип урока:    урок закрепления полученных знаний

 

Ход урока

 

1.Организационный момент урока: приветствие, настрой на урок.

 

Учитель:  Здравствуйте, 
                          Слово какое чудесное, 
                          Красивое, доброе, чуточку нежное. 
                         Здравствуйте! Скажем мы новому дню! 
                         Здравствуйте, скажем мы нашим гостям! 
                          Здоровья желаем всем и всему!

Улыбнитесь друг другу. И подумайте: как хорошо, что мы сегодня здесь все вме­сте. С таким чудесным настроением и начнем наш урок.

 

2.Мотивация урока. Сообщение темы, целей урока.

 

Учитель: Начать сегодняшний урок я решила издалека. В 1974 году астрономы попробовали проверить есть ли еще разумные существа во Вселенной. Потенциальным местом, там, где они могут жить, было выбрано звездное скопление в созвездии Геркулеса, которое состоит из сотен тысяч звезд возрастом близко 10 млрд. лет. Астрономы направили сильный радиосигнал, который вместил в себе 1679 различных сообщений. Расшифровав его, можно узнать про то, как выглядит человек, как построена наша Солнечная система, какие химические основы нашей человеческой биологии. В послании даже были закодированы некоторые произведения искусства и, естественно, самые значительные достижения науки. Среди базовых достижений науки была закодирована…теорема Пифагора.

-Как вы думаете, почему?

Не случайно и эпиграфом нашего урока являются слова великого Иоганна Кеплера: «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора».

-Чем мы займемся сегодня на уроке?

- Поэтому цель нашего урока: показать использование этого сокровища при решении не только задач, которые есть в учебнике, но и старинных задач и практических задач.

 

 

3. Актуализация опорных знаний, умений и навыков. Проверка д/з (до урока проводится учителем – максимум 4 балла)

 

Учитель: Урок сегодня у нас будет немного необычный – мы совершим увлекательное путешествие в страну «Пифагорию». С вашего разрешения, я буду вашим гидом, а вы моими помощниками. Билет: настроение. Смайлик. Оценка.

На нашей доске на память об этом путешествии мы будем крепить магнитики-наклейки. (на доске картинка ЧЕМОДАН)

1 ученик: Останавливаться надолго на биографии Пифагора мы не будем. 
Напомню лишь, что родился он на острове Самос около 580 года до н.э. Много путешествовал Египтом, пробыв там 22 года, изучал разные науки. Потом его, как пленного, отправили в Вавилон, где Пифагор находился 12 лет, изучая астрономию и астрологию. После плена переселился в Северной Италии и в Кротоне (греческой колонии) открыл известную Пифагорейскую школу. Пифагорейцы занимались математикой, философией, естественными науками. Пифагор говорил: «Числа управляют миром».

Учитель: Поэтому и начнем с вычислительной разминки.

 

Вычислительная разминка.

16	5	64	36
3	8	12	4
144	20	17	100
9	28	24	25

Закрасьте ячейки таблицы, в которых

 записаны значения выражений:

1) 4²;  2) 6²;  3) 3² ;  4) ;              

 

5) 8²; 6) ; 7) 3²+4²; 8) ;

 

9) 12²;   10) 6²+8²

- Молодцы, ребята. Действительно получилась буква «П».

Учитель: Эмблемой союза пифагорейцев является - пентаграмма - правильный пятиугольник. Считается, что он  обладает многими мистическими свойствами.  Это  символ  света и добра, жизни и здоровья.(картинка Пентаграмма крепится на чемодан).

 

Игра «Верю-не верю» (да-треугольник или нет-квадрат)
Вопросы 
1. В теореме Пифагора рассматривается  прямоугольный треугольник…

2. Катет длиннее гипотенузы…

3. В прямоугольном треугольнике все углы 90⁰…

4. Сумма острых углов в прямоугольном треугольнике равна 90⁰ …

5. Катет в прямоугольном треугольнике, лежащий против угла 30⁰ равен гипотенузе…

6. Треугольник прямоугольный, если его стороны равны 6; 8; 10…

Взаимопроверка: делим на 2.

 

Учитель: Во времена Пифагора теорема была сформулирована так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»

В связи с чертежом, сопровождавшим теорему Пифагора, ее также называли «ветряная мельница», составляя стишки вроде: Пифагоровы штаны во все стороны равны.(Картинка «Пифагоровы штаны» крепится на чемодан)

Учитель: К слову сказать, название «теорема» происходит от греческого слова «теорео», означавшего «рассматриваю» (от этого слова происходит и «театр»).

2 ученик: Современная формулировка теоремы Пифагора  «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

Существует шуточная формулировка теоремы.

Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим, 
Сумму степеней находим – 
И таким простым путем
К результату мы придем.

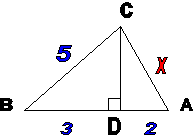
Рассмотреть теорему на рисунке.

 

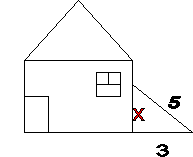
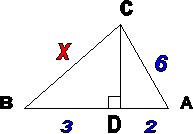
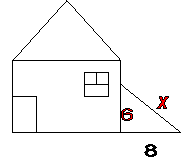
Устные решения задач по готовым чертежам.

Учитель: А вот доказательств этой теоремы на данный момент в научной литературе зафиксировано 367. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. И поэтому она внесена в книгу рекордов Гиннеса. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.(число 367 крепится на чемодан)

 

4. Решение задач по теме «Теорема Пифагора»

 Учитель: Осталось от теории перейти к практике. Где и как применялась, применяется и будет применяться теорема Пифагора? Почему актуальна в современной жизни?

На вопрос я отвечу отрывком из произведения немецкого писателя-романиста Адельберта Шамиссо о теореме Пифагора.

Суть истины вся в том, что нам она - навечно,

Когда хоть раз в прозрении её увидим свет,

И теорема Пифагора через столько лет

Для нас. Как для него, бесспорна, безупречна.

3 ученик:  В каких сферах деятельности применяется теорема Пифагора?

При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передача можно было принимать в определенном радиусе. В строительстве красивых здании в виде пирамид и параллелепипедов используется теорема Пифагора.

 

Задача 1. Из учебника «Арифметика» Леонтия Магницкого. Решение у доски.

Учитель: Ребята, знакомо ли вам имя  Леонтия Магницкого? Настоящая фамилия его – Телятин, а Магницким он стал по приказу Петра 1, который был восхищен его занятиями, притягивавшими к себе всех любознательных,  подобно магниту. Перед нами одна из его задач.

Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти нужно.

 

 

 

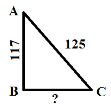
4 ученик:  Как говорит легенда, Пифагор был неплохим спортсменом и даже

чемпионом олимпийских игр по кулачному бою. Существует версия, что Пифагора сначала не хотели допускать до соревнований, говорили, что у него "ни роста, ни силы, ни внешности". "Да, – сказал на это Пифагор, – но я буду наносить удары с математической точностью!"

Учитель: Следующая старинная задача – не случайна. Пифагор оставил о себе память и в искусстве и в литературе. Можно верить, а можно и не верить, но легенды говорят, что Пифагор необыкновенно хорошо играл на арфе, увлекался стихами и был неплохим оратором. Поэтому задача – в виде стихотворения, принадлежит она древним индусам, у них был обычай формулировать задачи в стихотворной форме. 

Задача 2. Индийского математика XII века Бхаскары
              На берегу реки рос тополь одинокий.

• Вдруг ветра порыв его ствол надломал.
• Бедный тополь упал. И угол прямой
• С течением реки его ствол составлял.
• Верхушка склонилась у края реки.
• Осталось три фута всего от ствола.
• Запомни теперь, что в том месте река
• В четыре лишь фута была широка.
• Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

Справка:  от англ. foot — ступня — единица измерения длины в английской системе мер.  1 фут равен 0,3048 м

Дано:

ΔACD ()

AC=3 фута

AD=4 фута

CD=BC

Найти: AB. Ответ: 8 футов.

5 ученик: В средние века теорема Пифагора считалась настолько сложной, что ее называли pons asіnorum ("ослиный мостик"), или elefііga ("бегство никчемных"), поскольку дал еко не любой мог ее доказать, то есть перейти через "ослиный мостик". 

У математиков арабского востока эта теорема получила название "теоремы невесты". Дело в том, что в некоторых списках "Начал" Евклида эта теорема называлась "теоремой нимфы" за сходство чертежа с пчелкой, бабочкой, что по-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово "нимфа" как "невеста", а не "бабочка". Так появилось ласковое название знаменитой теоремы - "теорема невесты"» 

Учитель: Будем считать, что "ослиный мостик" мы с вами перешли. 

 

5. Видеопауза https://www.youtube.com/watch?v=kME6Gv5XVV8&t=1s

6 ученик: После его смерти ученики окружили имя своего учителя множеством легенд. Легенда о том, что в честь своего открытия (теоремы Пифагора) Пифагор принёс в жертву сто быков. 

Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящаются стихи, песни, рисунки, картины.

В Греции была выпущена почтовая марка по случаю переименования острова Самос в остров Пифагорейон. Эта марка – почти единственная среди многих тысяч существующих, на которой изображен математический факт.(картинка марки крепится на чемодан)

 

 

6. Самостоятельная работа (тест). Затем самопроверка- 4 балла.

Вариант 1	Вариант 2
1. К каким треугольникам можно применить теорему Пифагора? А) любым; Б) прямоугольным; В) равнобедренным; 2.Найдите расстояние до окна, к которому приставлена лестница.                      А) 8;         Б) 4;          В) не знаю. 3. Определите неизвестный элемент.                    А) ;          Б) 7;           В) 5. 4. Найдите AD. А) 20;          Б) 10;          В) не знаю.	1. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы? А) Нет;   Б) не знаю;  В)Да. 2.Какой длины должна быть лестница?                    А) 10;          Б) 14;          В) не знаю. 3. Определите неизвестный элемент.                 А)14;          б);           в) 4. 4. Найдите AD.        А) 14;          Б) 28;          В) не знаю.

 

7. Практическая задача с веревкой.

Учитель: Аристотель говорил: «Ум заключается не только в знании, но и в умении приложить знание на деле».

7 ученик: Считают, что теорему знали намного раньше. Так, за 1500 лет до Пифагора, жители Древнего Египта знали, что треугольник со сторонами 3, 4, 5 – прямоугольный и пользовались этим для построения прямых углов. Такой треугольник называется египетским. 

Предлагаю на несколько минут представить себя в роли древних египтян и показать, как это можно сделать. 

(Вызываются 3 человека, которые веревкой образовывают треугольник с прямым углом). Указание: в углах должны быть узлы.

- Молодцы! Вы достойно показали себя настоящими мастерами и, я надеюсь, что все полученные знания вам непременно пригодятся в дальнейшей жизни, например, когда решите построить свой дом.

 

8. Рефлексия «Синквейн»

Учитель:  А мы попробуем написать синквейн.  Это вид самоанализа, который позволит нам увидеть, чего мы сегодня достигли на уроке.

Стихотворение  состоит  из пяти строк. Первая строка- имя существительное, пусть это будет слово «ТЕОРЕМА ПИФАГОРА».

• Вторая строчка- 2 прилагательных.
• Третья строчка-3 глагола.
• Четвертая строчка - крылатая фраза.
• Пятая строчка- имя существительное, содержащее вывод.

-Что у вас получилось? А вот мой синквейн.

Теорема Пифагора
2. Строгая, логичная.
3. Строим, доказываем, вычисляем.
4. Квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.
5. Прямоугольный треугольник.

9. Д/з. Повторить п.16, решить №№540, 548.

Творческое задание: Составить прикладную задачу. Сообщение «Интересные страницы из жизни Пифагора».

 

10. Итоги урока. Оценивание (ученики суммируют баллы).

Учитель:  Сегодня вы сделали еще один шаг к тому, чтобы считать себя умным человеком. Даже египетские жрецы, отдавая своих детей на обучение, хотели, прежде всего, чтобы они изучали геометрию.

Вам идти в жизнь, вам доказывать не одну математическую, и не одну жизненную теорему. Может быть, со временем теорема Пифагора будет казаться вам до смеха простой. Но сегодня вы преодолели явный рубеж, вы стали умнее на целую теорему – на теорему Пифагора.