Урок геометрії 8 клас "Синус, косинус і тангенс гострого кута прямокутного трикутника"

Урок№1

Тема: Синус, косинус і тангенс гострого кута прямокутного трикутника

Мета:

• ввести поняття синуса, косинуса і тангенса гострого кута прямокутного трикутника, вчити обчислювати синус, косинус і тангенс гострого кута прямокутного трикутника;
• розвивати логічне мислення, вміння аналізувати, узагальнювати;
• виховання самостійності, акуратності записів.

Тип уроку: вивчення нового матеріалу.

Хід уроку

І. Організаційний момент. Мотивація

Доброго дня! Сідайте. Урок розпочати готові? Починаймо.

• Який сьогодні день?
• Який це по рахунку день тижня?
• Який зараз урок? Урок триває 45 годин?
• Трикутник – геометрична фігура?
• Як називається трикутник, у якого є один прямий кут?
• Чому дорівнює градусна міра прямого кута?
• Вчора я йшла і знайшла трикутник з двома прямими кутами. Ви мені вірите? (відповіді учнів з обґрунтуванням)
• Якщо трикутник прямокутний то два інші кути у нього які? (гострі)

Сьогодні ми дамо визначення синуса, косинуса і тангенса гострого кута прямокутного трикутника та навчимось знаходити синус, косинус і тангенс гострих кутів прямокутних трикутників. Але у вас може виникнути питання: «Навіщо це нам потрібно?» Деякі життєві задачі не можливо вирішити без даних знань. Наприклад: як виміряти висоту сонця над горизонтом? Як визначити довжину мосту, який потрібно збудувати через широку річку? Як розв’язати задачу: «З маяка висотою 70 метрів видно корабель під кутом 3 градуси до горизонту. Яка відстань від маяка до корабля?» Щоб відповісти на всі ці та багато інших питань нам і потрібні будуть сьогоднішні знання, здобуті на уроці.

ІІ. Актуалізація опорних знань

1. Який трикутник зображений на рисунку є прямокутним?

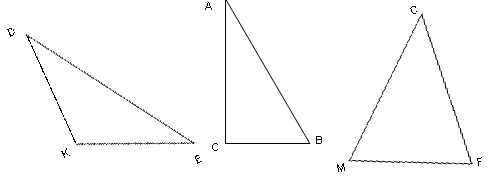
2. Зобразіть цей трикутник в зошитах. Як називаються сторони AB, BC, AC?
3. Назвіть катет, прилеглий до кута А, протилежний до кута А.
4. Назвіть катет прилеглий до кута В, протилежний до кута В.

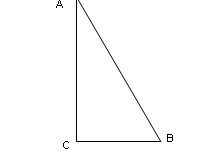В зошитах учнів і на дошці має з’явитись запис:

АВ – гіпотенуза, АС і ВС – катети.

Для кута А: АС – прилеглий катет, ВС – протилежний.

Для кута В: ВС – прилеглий катет, АС – протилежний.

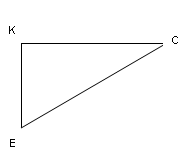
5. Диктант (на окремих листках з подальшою взаємоперевіркою)

1. Назвіть:

1. гіпотенузу
2. катети
3. катет протилежний куту Е
4. катет прилеглий до кута Е

2. Продовжіть  речення: сторона прямокутного трикутника, що лежить проти кута 90° називається…
3. Продовжіть  речення: сторони прямокутника, що утворюють прямий кут називаються…

ІІІ. Вивчення нового матеріалу

Сьогодні ми працюватимемо в групах. Мета нашої роботи – виявити суттєві особливості деяких відношень довжин сторін прямокутного трикутника. Щоб розпочати роботу, потрібно накреслити два прямокутні трикутники, з рівними гострими кутами. Тут ми вдамося до певних хитрощів: ми,  немов би «накладемо» накладемо ці трикутники один на одного. Наприклад:

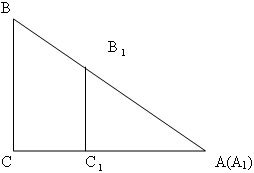
Працювати ви будете згідно плану, записаному на аркушах, що лежать у вас на столах:

1. Накресліть трикутники, як показано на прикладі.

• Виміряйте довжини вказаних сторін трикутників в мм і обрахуйте їх відношення за допомогою мікрокалькуляторів, з точністю 4 – х знаків після коми.

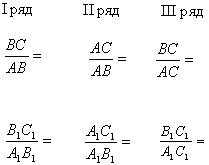
2. Порівняйте отримані результати з результатами в своїй групі.
3. Округліть отримані результати до десятих і порівняйте наступні відношення.

І ряд                          ІІ ряд                     ІІІ ряд

                                      

4. Оцініть розташування вказаних сторін по відношенню до гострого кута А (протилежна, прилегла) та один до одного (катет, гіпотенуза).

5. Як ви думаєте:

• Результати отримані в п.3 – це випадковість чи ні?
• Значення відношень залежать від довжин сторін чи від величини кута?

Після обговорення доходимо до висновку, що отримані результати залежать від величини  гострого кута і не залежать від розмірів трикутника.

Тепер доповнюємо записи учнів такими відношеннями:

6. Спробуйте визначити, які саме відношення ви знаходили в своїй групі. Сформулюйте висновки, використовуючи поняття «прилеглий катет», «протилежний катет». (відповіді учнів)
7. Отже, якщо в двох прямокутних трикутниках гострі кути рівні, то відношення:

• Протилежного катета до гіпотенузи;
• Прилеглого катета до гіпотенузи;
• Протилежного катета до прилеглого – рівні.

Висновок: в прямокутному трикутнику відношення довжин двох сторін не залежать від їх довжини, а залежить лише від величини гострого кута. Тому такі відношення не залишились поза увагою, їм дали назву синус, косинус і тангенс.

Завдання учням:

1. Знайдіть в підручнику означення синуса і прочитайте.
2. Знайдіть в підручнику означення косинуса  і прочитайте.
3. Знайдіть в підручнику означення тангенса і прочитайте.

Скажіть, що саме ви знаходили в своїй групі? (синус, косинус чи тангенс)

Синус, косинус і тангенс – це тригонометричні функції. Термін «тригонометрія» означає дослівно «трикутниковимірювання» або виміри в трикутнику.

ІV. Первинне закріплення нових знань учнів

1. Заповніть пропуски:

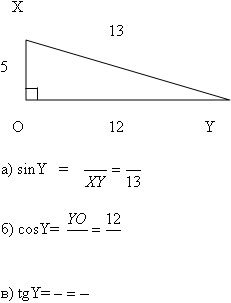
2. Знайдіть:

а) sinX =

б) cosX =

в) tgX =

Розглянемо деякі властивості тригонометричних функцій.

1. Продовжіть рівність: 

Перевірте рівність

sin²X  + cos²X = 1.

Отже,  sin²α  + cos²α = 1.

Ми отримали рівність, яку називають основною тригонометричною тотожністю.

2. Перетворіть наступне відношення:

Таким чином ми отримали ще одне означення тангенса:

V. Підсумок уроку

VІ. Домашнє завдання:

Вивчити: п.17, ст.124

Виконати: №582,586,590,592. (підручник за ред.Мерзляк)