Урок геометрії 8 клас + презентація "Теорема Фалеса"

Тема: Теорема Фалеса

Мета:  довести теорему Фалеса, навчити застосовувати її при розв’язуванні задач;  розвивати вміння застосовувати свої знання на практиці; прививати пізнавальний інтерес до предмету.

Тип уроку:  засвоєння нових знань

Хід уроку

І. Організаційний момент

• Перевірити готовність учнів до уроку
• Перевірити відсутніх

ІІ. Мотивація навчальної діяльності

• Геометрія – одна з древніх наук і її розвиток бере свій початок у далекому минулому. Він почався з елементарних понять математики, з практичних потреб людей і дійшов до нас у такому сучасному вигляді, в якому ми сьогодні розглядаємо цю науку. Дуже багато математиків працювали в цій галузі. Вони були філософи і математики водночас, юристи і математики, філологи і математики. Нажаль, ми не дуже багато знаємо про математиків, які внесли свій вклад в розвиток цієї науки. Однак є багато теорем, що носять назву математика, який не тільки придумав теорему, але й довів її.
• Перша теорема, яка носить назву вченого, що придумав і довів її, і яку ми будемо вивчати в шкільному курсі геометрія – теорема Фалеса.
• У нас є учні, які приготували презентацію про нього.

Учнівська презентація

ІІІ. Актуалізація опорних знань

• Перед  тим, як розпочати вивчення нової теми, давайте пригадаємо деякі  факти, які допоможуть вам засвоїти нові знання.

Фронтальне опитування:

1. Які відрізки називаються рівними (два відрізки називаються рівними, якщо вони суміщаються при накладанні або мають однакові довжини)
2. За допомогою яких креслярських інструментів можна відкласти рівні відрізки? (лінійки з поділками або циркуля)
3. Які прямі називаються паралельними? (дві прямі, які на площині не перетинаються називаються паралельними)
4. Сформулюйте ознаки паралельності прямих? (1. Якщо внутрішні різносторонні кути, утворені при перетині прямих з січною – рівні, то прямі паралельні. 2. Якщо внутрішні односторонні кути,утворені  при перетині прямих з січною в сумі становлять 180°, то прямі паралельні. 3. Якщо відповідні кути,утворені  при перетині прямих з січною – рівні, то прямі паралельні.)
5. Скільки ознак рівності трикутників ви знаєте? (три)
6. Сформулюйте  І ознаку рівності трикутників. (два трикутники називаються рівними, якщо дві сторони і кут між ними одного трикутника = відповідним двом сторонам і куту між ними другого трикутника)
7. Сформулюйте ІІ ознаку рівності трикутників. (Якщо сторона і два прилеглі до неї кути одного трикутника = відповідним стороні і двом прилеглим кутам другого трикутника, то такі трикутники рівні)
8. Сформулюйте третю ознаку рівності трикутників. (якщо три сторони одного трикутника = трьом сторонам другого трикутника то такі трикутники – рівні.)

IV. Вивчення нового матеріалу

• Записали число, класна робота і тему уроку: «Теорема Фалеса»

План:

1. Теорема Фалеса та її доведення
2. Задача на застосування теореми Фалеса
3. Поділ даного відрізка на n рівних частин.
4. Задача на поділ відрізка на рівні частини.

1. (Слайд 1)Теорема Фалеса формулюється так: якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій стороні кута.

• Кожна теорема має умову (те, що дано) і висновок (те, що потрібно довести), тому давайте розберемо, що нам дано:

1. Нехай нам даний кут АВС.
2. На стороні АВ відкладемо рівні відрізки: МК і КР та через кінці цих відрізків (тобто через точки М і К) проведемо паралельні прямі МО, КЕ, РН.
3. Нам потрібно довести, що ОЕ = ЕН.

• Для того, щоб ми могли це зробити, виконаємо додаткову побудову.

4. Проведемо через т.К пряму ХТ, яка буде паралельна стороні кута – ВС. (Які фігури утворились?)
5. При цьому у нас утворилось два чотирикутники: ОХКЕ і ЕКТН. Ці чотирикутники будуть паралелограмами, тому що ХК 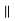ОЕ і КТ 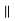ЕН – за побудовою і ХО 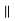КЕ та КЕ 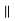ТН – за умовою, як відрізки, що лежать на паралельних прямих.
6. Розглянемо ∆ХКМ і ∆ТКР. В них:  ХКМ =  ТКР – як вертикальні кути, МК = КР – за умовою, та  ХМК = ТРК – як внутрішні різносторонні кути при паралельних прямих МО і РН та січній АВ.
7. Отже, ∆ ХКМ = ∆ТКР – за стороною і двома прилеглими кутами.
8. З рівності трикутників слідує рівність відповідних сторін, а саме ХК = КТ.
9. Тоді ХК = ОЕ = КТ = ЕН. Що й треба було довести.

(Кілька дітей формулюють теорему)

• На використання цієї теореми розв’яжемо усно задачу.

(слайд 2)

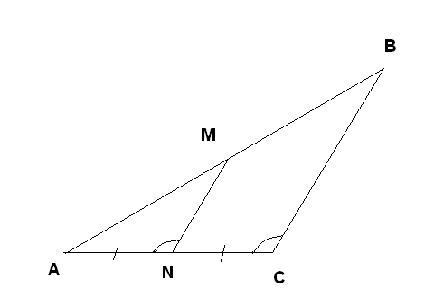
Задача №1.

Дано:∆АВС,  ANM =  ACB = 116°,

AN = NC, AM = 14 см.

Знайти: АВ.

• У мене в руках є паперова смужка довжиною 5 дм. Скажіть: як її поділити на дві рівні частини, не маючи лінійки? (Скласти її навпіл і розрізати)
• А на 4 рівні частини? (Кожну новоутворену смужку знову скласти навпіл і розрізати)
• А на 5 рівних частин? (не знаєте?)
• Теорема Фалеса допоможе нам це зробити.

2. (слайд 3) Задача: поділіть відрізок на 5 рівних частин.

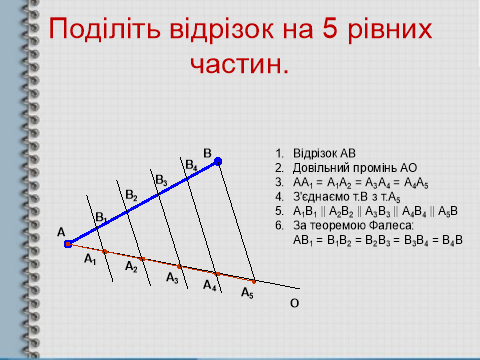
• Скажіть: а чи можна поділити довільний відрізок на 9 рівних частин? На 100 рівних частин?
• Отже, за допомогою теореми Фалеса ми можемо поділити довільний відрізок на будь – яку кількість рівних частин.

V. Розв’язування задач за готовими рисунками

(слайд 5) 

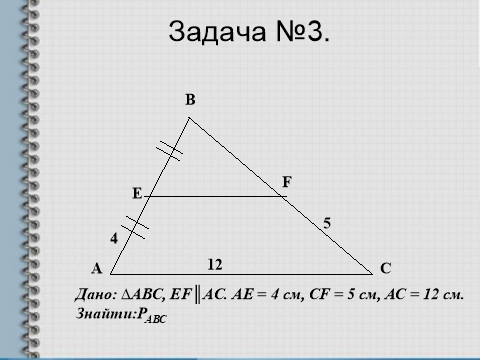
(слайд 6)

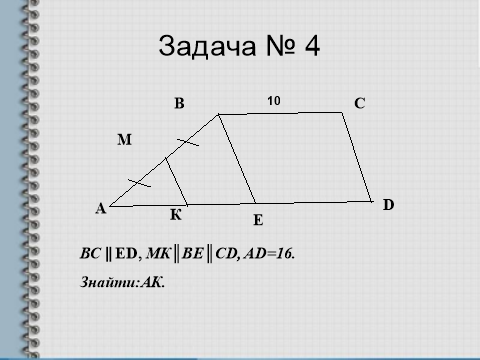
VI. Підсумок уроку

• Що нового ви вивчили сьогодні на уроці? (теорему Фалеса)
• Сформулюйте теорему Фалеса.
• Як можна застосувати її? (поділити відрізок на рівні частини, та при  розв’язуванні різних геометричних задач)

Урок  я хотіла б завершити влучними словами Фалеса Мілетського:

1. Завжди і у всіх учись кращому.
2. Всесвіт знаходиться всередині людини – в його розумовій творчості.

VII. Д/з (Слайд 7)