Урок, Геометрія, Скалярний добуток векторів, 9 клас.

Тема : Скалярний добуток векторів.

Мета : Сформувати поняття  скалярного добутку векторів; домогтися засвоєння  властивостей скалярного добутку векторів і сформувати вміння використовувати  поняття скалярного добутку векторів для розв’язування задач.

  Розвивати логічне , раціональне й критичнее мислення;  створювати умови для  «ситуації успіху»; розвивати слухову , зорову та тактичну пам’ять ; формувати атмосферу співдружності.

   Виховувати працьовитість,  математичну  культуру, об’єктивність в оцінюванні результатів власної й колективної праці.

   Тип уроку: засвоєння знань , умінь і навичок.

Обладнання: мультимедійна дошка ; індивідуальні картки із завданням; таблиця «Вектори на площині».

Девіз уроку: Думаємо колективно , працюємо оперативно, сперечаємось доказово – це для всіх обов’язково.

Хід уроку

І.Актуалізація опорних знань.

1. Перевірка домашнього завдання.

Два учні біля дошки пояснюють виконання домашніх задач. Учні класу слухають та перевірять свої записи, задають запитання по ходу розв’язку.

2. Робота за індивідуальними картками.

№1.

1. Абсолютна величина вектора ā(5;m) дорівнює 13, а вектора b (n;24) дорівнює 25. Знайти m і n.

2.Знайти вектор с=2ā-3b,якщо ā(-2;6) , b(5;-3).

№2.

1 Абсолютна величина вектора  λā дорівнює 25. Знайдіть λ, якщо       ā(-6;8).

2. Знайти вектор с=-3ā +4b, якщо ā(-2;6) , b(5;-3).

3. Фронтальне опитування

(під час фронтального опитування, використовується мультимедійна система, програма «Геометрія 7-9» з теми «Вектори на площині» та відповідні інтерактивні моделі. Учні відповідають на запитання і де можливо використовують інтерактивні моделі).

- Що називається вектором?

- Що називається модулем вектора?

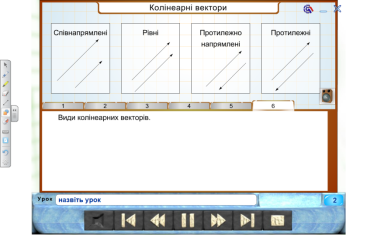
- Які вектори називаються колінеарними? Види колінеарних векторів.

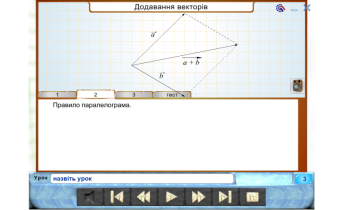
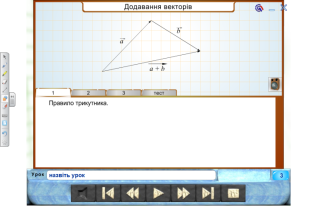
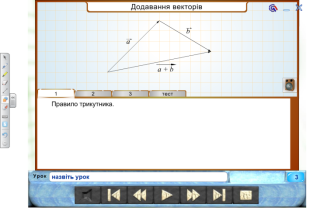
- Які є геометричні способи додавання та віднімання векторів, множення вектора на число.

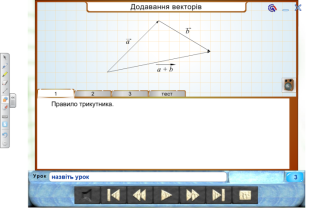
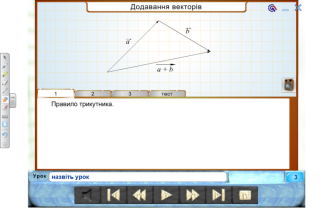
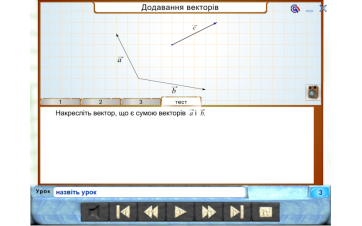
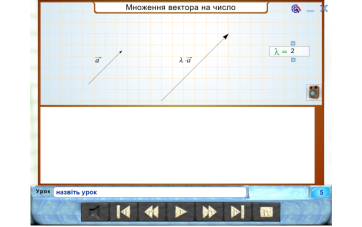
- Як знайти координати вектора , коли відомі координати його кінців?

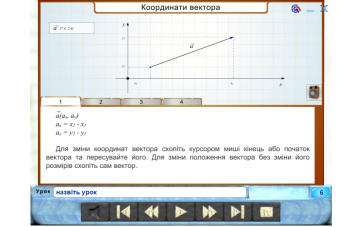
- Як знайти суму (різницю) векторів, якщо відомо їх координати?

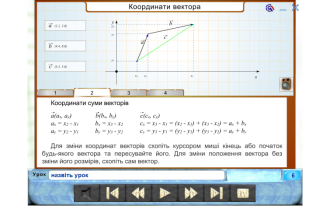
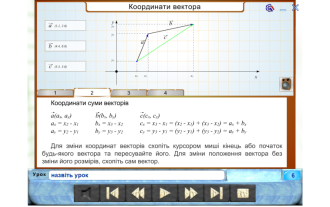
ІІ. Вивчення нового матеріалу.

План .

1. Кут між векторами.

2. Поняття скалярного добутку векторів.

3. Умова рівності нулю скалярного добутку векторів.

4. Формула для знаходження кута між векторами.

5. Розв’язування задач.

   Вивчаючи новий матеріал, скористуємось електронним підручником  програми «Геометрія 9» з теми «Скалярний добуток векторів» та прослухаємо пояснення коментатора.

1.Кут між векторами.

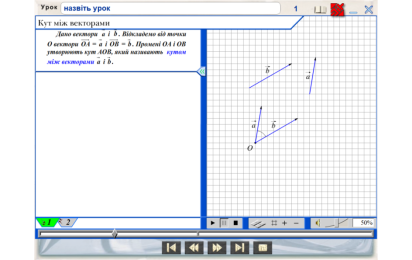
Після прослуховування цього пункту учні самостійно знаходять кут між співнапрямленими та протилежно напрямленими векторами.

2. Поняття скалярного добутку векторів.

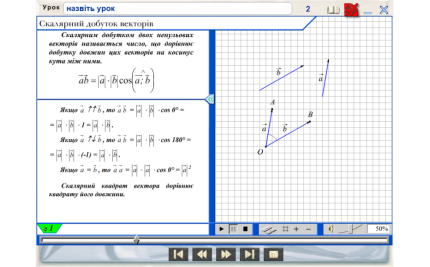
Коментар вчителя про скалярний добуток , якщо вектори спів -напрямлені  та протилежно напрямлені.

3.Умова перпендикулярності двох векторів.

     Доведення прямої теореми прослуховується за електронним підручником.

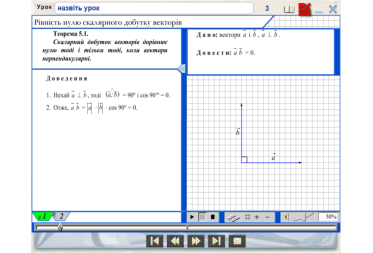
    Обернену теорему учні самостійно доводять у зошитах і коментують біля дошки , використовуючи кадр із програми.

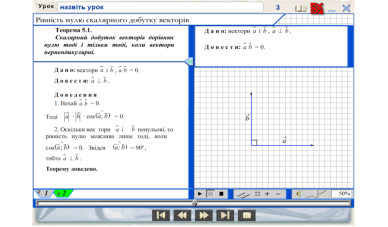
4.Вивчення формули для знаходження кута між векторами (використання кадра «Формула для знаходження кута між векторами).

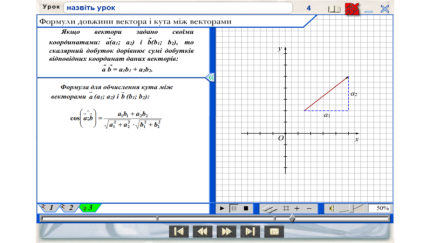
ІІІ. Закріплення знань та вмінь.

Робота з підручником.

    -  Усно. Метод «Прес».

Виконання вправ : №842, 843.

    - Письмово. Колективно.

1. Знайдіть кут між векторами ā(2;0) і b(2;2).

2. При якому значенні m вектори ā(-2;3) і b(2;m) перпендикулярні?

ІV. Підсумок уроку.

Рефлексія .Вправа  «Мікрофон».

Чи вдалося відчути себе успішним на уроці?

V. Домашнє завдання

п. 25,вивчити. Виконати №860 (2), № 850(2), №862(2).

Література.

1. М.І. Бурда , Геометрія-9, Київ «Зодіак -ЕКО»2009.

2. О. Пометун,  Л. Пироженко, «Сучасний урок . Інтерактивні технології  навчання», Київ, «А.С.К.» 2005.

3. Журнал «Математика в школі» №10, 2010.