Урок "Графік лінійного рівняння з двома змінними"

Тема: Графік лінійного рівняння з двома змінними.

Мета: дати означення графіка лінійного рівняння з двома змінними; розробити алгоритм побудови графіка лінійного рівняння з двома змінними, розглянути всі можливі випадки розміщення графіка відносно системи координат, виробити вміння будувати лінійне рівняння з двома змінними; формувати уміння робити вибір рівня завдання при розв’язуванні вправ; розвивати інтерес до вивчення предмета, завдяки використанню комп’ютера, розвивати розумову діяльність; виховувати самостійність і взаємоповагу.

Тип уроку: Урок вивчення нового матеріалу.

Хід уроку

І. Актуалізація опорних знань.

Добрий день. Сьогодні у нас урок вивчення нового матеріалу, але спочатку ми розглянемо декілька завдань на повторення. Пограємо з вами у гру «Математичне лото».

У вас на партах є картки, в клітинках яких записані завдання, що необхідно розв’язати. Ви записуєте коротеньке розв’язання у зошит ( якщо це необхідно), а знайшовши відповідь, накриваєте завдання карткою. На звороті кожної картки літера. Таким чином. розв’язавши всі завдання ви отримаєте імена відомих людей.

Завдання до гри:

1 варіант (Діофант)

1. Функцію задано формулою . Яке значення функції відповідає значенню аргументу  -3?	2. Для якого значення аргументу значення функції дорівнює 4, якщо функцію задано формулою ?	3. Функцію задано таблично х -2 4 0 -2 -4 у -1 -3 5 3 1 Для яких значень функції  значення аргументу дорівнює -2?
4. Яка з точок належить графіку функції ?	5. Які  координати точок перетину графіка функції з осями координат?	6. Графік функції перетинає вісь абсцис у точці (-1,5;0). Знайдіть значення .

2 варіант (Декарт)

1. Функцію задано формулою . Яке значення функції відповідає значенню аргументу  3?	2. Для якого значення аргументу значення функції дорівнює 5, якщо функцію задано формулою ?	3. Функцію задано таблично х 0 1 -1 2 -2 у 3 2 2 1 1 Для яких значень аргументу значення функції дорівнює 2?
4. Яка з точок належить графіку функції ?	5. Які  координати точок перетину графіка функції з осями координат?	6. Графік функції перетинає вісь ординат у точці (0;3). Знайдіть значення .

 

Отже, які слова після розв’язання завдань ви отримали?  (Декарт, Діофант)

Зараз прослухаємо повідомлення про цих видатних математиків, які нам підготували…

 

Діофант (ІІІ ст.) – один із засновників алгебри. Жив і працював в Олександрії. Про його життя майже нічого невідомо. Але все що відомо про його життя взято із напису на його гробниці «Подорожній! Тут прах похований Діофанта. І числа розповісти можуть, о диво, як довго життя його тривало. Частина шоста промайнула прекрасним дитинством. Дванадцята частина життя ще пройшла – покрилось пушком тоді підборіддя. Сьому в бездітному шлюбі провів Діофант. Пройшло п’ятиріччя: він був щасливий народженням прекрасного первістка-сина. Якому доля лише половину життя чудового і світлого дала порівняно з батьком. І в горі глибокім старець земного життя кінець прийняв, проживши лиш років чотири з тих пір, без сина зостався.»

 Збереглась лише частина його трактату «Арифметика» (6 книг із 13), де подається розв’язання задач, які в більшості зводяться до невизначених рівнянь, тобто рівнянь з двома змінними. Діофант розглядав рівняння з двома змінними в множині цілих чисел, тобто визначав такі розв’язки, що є парами цілих чисел. Згодом такі рівняння почали називати діофантовими. Він останній із математиків античності.

 

Про те скільки років прожив Діофант ми дізнаємось пізніше.

Про Декарта відомо набагато більше.

Рене Декарт — французький філософ, матема­тик, фізик. Дворянин за походженням, народився 1596 року. Він не відразу знайшов своє місце в житті. Після закінчення коледжу у 1612 р. спочатку готувався до військової кар'єри, пізніше пори­нув у світське життя, подорожував країнами Євро­пи, потім все кинув заради науки.

Декарт намагався і в філософії і в будь-якій іншій науці знайти математичні закони, звести кож­не питання або кожну задачу до математичної.

У 1637 р. вийшла книжка Р.Декарта «Міркуван­ня про метод», у якій поряд із загальними філо­софськими міркуваннями про матерію значну ува­гу приділено «універсальній математиці». В одно­му з розділів автор запропонував новий метод - метод координат, який дав можливість переходити від точки (у координатній площині) до пари чисел, від лінії до рівняння, від геометрії до алгебри. Це була нова геометрія, яку зараз називають аналітич­ною геометрією.

Заслуга Р.Декарта полягає також у тому, що він увів позначення, які збереглися до нашого часу: ла­тинські букви х, у, z — для змінних; а, b, с — для коефіцієнтів. Завдяки цьому кожній прямій у коор­динатній площині відповідає лінійне рівняння ах +  by = с (де а або b відмінні від нуля числа) і навпаки.

Метод координат дає змогу будувати графіки рівнянь, зображати геометричне залежності, вира­жені за допомогою рівнянь і формул, розв'язувати геометричні задачі за допомогою алгебри.

З іменем Декарта ми будемо зустрічатися, вивча­ючи механіку, оптику, біологію. З 1628 р. Декарт жив у Голландії, у 1619 р. переїхав у Швецію, де і помер від пневмонії у 1650 р.

 

 

ІІ. Повідомлення теми і мети уроку

І так, як ви здогадались, говорити ми з вами будемо про лінійні рівняння з двома змінними. і не просто їх розв’язувати, а будувати їх графіки.

Отже, основна метою нашого уроку навчитися будувати графіки такого типу рівнянь.

Запишемо в зошитах число, класна робота, тема нашого уроку «Графік лінійного рівняння з двома змінними»

 

ІII. Вивчення нового матеріалу.

У вас на партах є опорні конспекти, які  ви вклеїте у свої зошити для конспектів. А зараз вони вам стануть на допомозі при вивченні нової теми. Починаємо…

- рівняння першого степеня з двома змінними, де

Виразимо змінну у через змінну х.

Одержимо: - це формула лінійної функції.

Отже, графік кожного рівняння першого степеня  з двома змінними – пряма. І кожна пряма – графік деякого лінійного рівняння з двома змінними.

 

 

Алгоритм побудови графіка лінійного рівняння з двома змінними

1. Виразити змінну у через змінну х.

2. Підібрати два значення змінної х.

3. Обчислити відповідні значення змінної у.

4. Позначити на координатній площині відповідні їм точки.

5. Провести пряму через дві точки.

Приклад

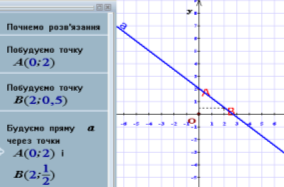
Побудувати графік рівняння .

Виразимо з рівняння змінну у через змінну х:  .

Якщо , то ; якщо , то .

Позначимо в прямокутній системі координат точки (0; 2) і (2; 0,5) та проведемо через них пряму.

 

 

Розміщення графіка лінійного рівняння з двома змінними  відносно системи координат

 

Умова	Приклад	Висновок
Якщо a=0, b≠0, c≠0 , то рівняння ax+by=c має вигляд:  by=c, звідки		Графіком даного рівняння є пряма паралельна осі х
Якщо b=0, a≠0, c≠0 , то рівняння ax+by=c має вигляд: ax=c, звідки		Графіком даного рівняння є пряма паралельна осі y
Якщо с=0, a≠0, b≠0 , то рівняння ax+by=c має вигляд:   ax+by=0, звідки		Графіком даного рівняння є пряма, що проходить через початок координат
Якщо a=0, b=0, c=0 , то рівняння ax+by=c має вигляд: 0x+0y=0		Рівняння задовольняє будь-яка пара чисел. Графіком є вся координатна площина.
Якщо a=0, b=0, c≠0 , то рівняння ax+by=c має вигляд: 0x+0y=с		Рівняння не має жодного розв'язку

IV. Закріплення нового матеріалу.

1) Усні вправи:

Що є графіком рівняння і скільки воно має розв’язків:

1)   (рівняння не має жодного розв’язку)

2)     (рівняння задовольняє будь-яка пара чисел; графіком є вся координатна площина);

3)      (рівняння має безліч розв’язків (абсцисою є будь-яке число, а ордината 2,5), графіком є пряма паралельна осі х);

4)      (рівняння має безліч розв’язків(абсциса 2, ордината будь-яке число), графіком є пряма паралельна осі у);

5)   (рівняння має безліч розв’язків (абсциси яких протилежні ординатам), графіком є пряма що проходить через початок координат);

6)   (рівняння має безліч розв’язків, графіком є пряма)

 

2) Письмові вправи:

Ми з вами працюємо по групах.

(група А виконує завдання середнього рівня.

Група Б виконує завдання достатнього рівня)

(Завдання записані на дошці)

Для того, щоб дізнатися кому належить вислів «У математичних питаннях не можна нехтувати й найменшими похибками» вам потрібно розгадати шифрограму:

А	Ь	Т	О	Н	Ю	С
(-1; 0)	(2; 1,5)	(1; 0)	(0; 0)	(-3; 2)	(0; 5)	(0; 2)

Відповідь: Ісаак Ньютон

Група А 

№ 1

Чи належить точка А(-3;2) графіку рівняння:  5х+12у=9

Розв’язання

Підставимо координати т. А у рівняння графіка

, , 9=9.

Точка А належить графіку рівняння.

 

№ 2

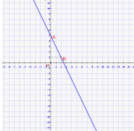
Побудуйте графік рівняння 2х+у=5

Розв’язання

Виразимо змінну у через змінну х .

Якщо х=0,  то ,

Якщо х=2, то .

Позначимо в прямокутній системі координат точки (0; 5), (2; 1)та проведемо прямі через ці точки.

 

Група Б.

№ 1.

Точка з ординатою 1,5 належить графіку рівняння 5х+4у=16. Знайдіть абсцису цієї точки.

Розв’язання

оскільки точка з ординатою у=1,5 належить графіку даного рівняння, то підставимо дане значення у рівняння.

, , ,  .

Відповідь: 2

 

№ 2.

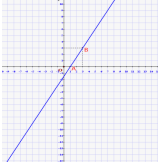
Побудуйте графік рівняння 3х-2у=3

Розв’язання

Виразимо змінну у через змінну х .

Якщо х=1,  то ,

Якщо х=3, то .

Позначимо в прямокутній системі координат точки (1; 0), (3; 3) та проведемо прямі через ці точки.

 

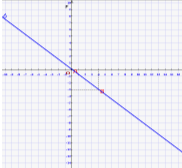
Побудуйте графік рівняння   1,5х+2у=0

Розв’язання

Виразимо змінну у через змінну х .

Якщо х=0,  то ,

Якщо х=4, то .

Позначимо в прямокутній системі координат точки (0; 0), (4; -3) та проведемо прямі через ці точки.

 Програма по побудові графіка рівняння

V. Повідомлення домашнього завдання.

(завдання записане на звороті дошки).

Опрацювати конспект.

Група А:

Група Б:

 

VI. Підсумок уроку.

Гра «Третій зайвий»

1. Лінійним рівнянням з двома змінними є:

1) ;

2) ;

3) .

2. Яка точка належить графіку рівняння :

1) А(2; 1);

2) В(-2; 1);

3) С(2,5; 2)

3. Графіком якого рівняння є пряма паралельно осі х:

1) ;

2) ;

3) .

4. Графіком якого рівняння є пряма, яка проходить через початок координат:

1) ;

2) ;

3) .

5. Графіком якого рівняння є пряма паралельна осі у:

1) ;

2) ;

3) .

VII. Додаткова задача.

Розв’язати задачу про життя Діофанта.

 

Рідною мовою	Мовою алгебри
Подорожній! Тут прах похований Діофанта. І числа розповісти можуть, о диво, як довго життя його тривало	x
Частина шоста його промайнула прекрасним дитинством
Дванадцята частина життя ще пройшла — покрилось пушком тоді підборіддя
Сьому в бездітному шлюбі провів Діофант
Пройшло п'ятиріччя: він був щасливий народженням прекрасного первістка-сина	5
Якому доля лише половину життя чудового і світлого дала порівняно з батьком
І в горі глибокім старець земного життя кінець прийняв, проживши лиш років чотири з тих пір, як без сина зостався	4
Скажи, скільки років життя досягнувши, смерть прийняв Діофант?

 

Розв'язавши рівняння і знайшовши, що х = 84, дізнаємося такі епізоди біографії Діофанта: він одружився у 21 рік, став батьком у 38 років, втра­тив сина у 80 років.

 

 

Математика – це мистецтво

давати однакову назву різним речам…

Доведення, зроблені для певного об'єкта,

безпосередньо застосовані до багатьох

 нових об'єктів без подальших змін.

А. Пуанкаре