Урок " Графік нерівності з двома змінними"
Формувати в учнів уміння будувати графіки нерівностей з двома змінними та за видом графіків, зображених на рисунках, визначати нерівність.ормувати в учнів уміння будувати графіки нерівностей з двома змінним та за видом графіків, зображених на рисунках, визначати нерівність.формувати вміння переносити набуті знання в нові ситуації.
Ввиховувати культуру математичних міркувань, працьовитість, самостійність. комп'ютери, програма “Advanced Grapher", картки з алгоритмом розв'язування нерівностей з двома змінними, індивідуальні завдання.
Тема: “Графік нерівності з двома змінними”
Виховна мета: формувати в учнів уміння будувати графіки нерівностей з двома змінними та за видом графіків, зображених на рисунках, визначати нерівність.
Розвивальна мета: формувати вміння переносити набуті знання в нові ситуації.
Виховна мета: виховувати культуру математичних міркувань, працьовитість, самостійність.
Обладнання: комп’ютери, програма “Advanced Grapher”, картки з алгоритмом розв’язування нерівностей з двома змінними, індивідуальні завдання.
Хід уроку
І Організаційний момент.
ІІ Перевірка домашнього завдання.
Перевірку домашнього завдання учитель організує на персональних комп’ютерах за допомогою програми “Advanced Grapher” із обов’язковим коментуванням учнями.
Після роботи за зразком учні виконують корекцію своїх розв’язань у робочих зошитах.
№1 Покажіть штриховкою на координатній площині множину точок, координати яких задовольняють системі:
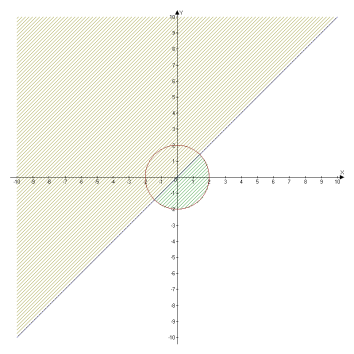 а)
а) 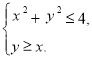

б) 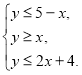
№2 Побудувати графік рівняння:
![]()
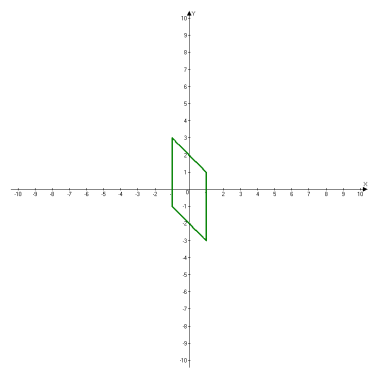
Під час перевірки домашнього завдання учні згадують алгоритм графічного рівняння нерівності з двома змінними.
ІІІ Актуалізація опорних знань.
1. Фронтальне опитування
а) Що називається нерівністю з двома змінними?
б) Що називається розв’язком нерівності з двома змінними?
в) Що називається графіком рівняння з двома змінними? Що називається графіком нерівності з двома змінними?
г) Як, знаючи графік функції ![]() , побудувати графік нерівності
, побудувати графік нерівності ![]()
![]() та нерівності
та нерівності ![]() ?
?
д) Поясніть на прикладі, як можна знайти на координатній площині множину точок, координати яких задовольняють нерівність з двома змінними.
Тестова діагностична робота за персональними комп’ютерами.
Кожній правильній відповіді відповідає буква. З отриманих букв скласти слово.
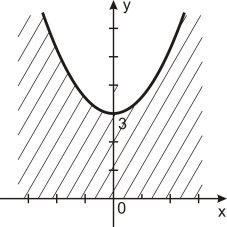
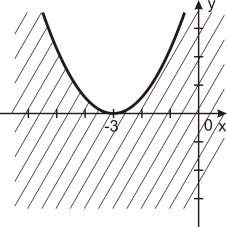
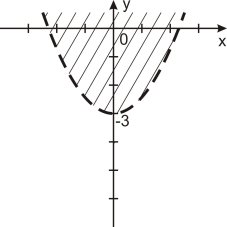
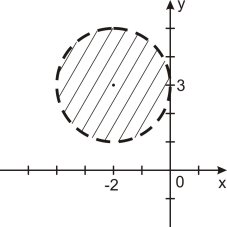
1. Укажіть, на якому рисунку зображено графічний розв’язок нерівності
y > x2 – 3
|
Б) |
|
Д) |
|
|
|
|
|
|
|
М)
|
|
Р) |
|
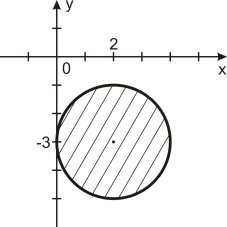
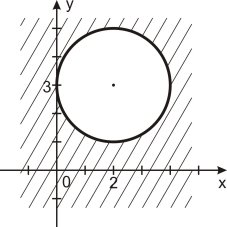
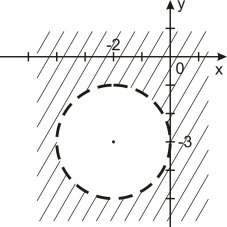
2. Укажіть на якому рисунку зображено графічний розв’язок нерівності
(х - 2)2 + (у + 3)2 ≤ 4
|
А) |
|
Е) |
|
|
|
|
|
|
|
К)
|
|
Т) |
|
3. За рисунком визначити нерівність

|
Н) у ≥ │х – 2│ |
Т) у < │х│ + 2 |
О) у ≥ │х│ - 2 |
Л) у ≤ │х + 2│ |
4. При якому а нерівність х2 + 5 < а не має розв’язків.
|
В) а = 5 |
Е) а є (-∞ ; 5) |
А) а є (-∞ ; 0) |
Ф) а є (5 ; ∞) |
Отримали закодоване слово РЕНЕ, якщо вірно виконали тест. РЕНЕ – ім’я відомого французького математика Декарта. Пропонується відкрити папку під назвою «Біографія». Учень робить повідомлення вигляді презентації.
Рене Декарт
|
|
Рене́ Дека́рт (фр. René Descartes, лат. Renatus Cartesius — Картезій; *31 березня 1596, Ла-Е-ан-Турен (фр. La Haye en Touraine) [зараз місто Декарт], департамент Ендр і Луара, Франція — †11 лютого 1650, Стокгольм) — французький філософ, фізик, фізіолог, математик, основоположник аналітичної геометрії. У математиці Декарт запровадив Декартову систему координат, дав поняття змінної величини і функції, ввів багато алгебраїчних позначень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. Декарт — автор методу радикального сумніву в філософії, механіцизму у физиці, передтеча рефлексології.
|
Афоризм
«Все науки настолько связаны между собою, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех прочих»
Учитель підкреслює, що найважливішим досягненням Р.Декарта було створення нового методу математичного досягнення – метод координат. Цей метод дає змогу ефективним засобом досліджувати рівняння на існування та кількість розв’язків, розв’язувати рівняння та нерівності з двома змінними, задачі з параметрами, звертаючись до відповідних графічних інтерпретацій на координатній площині.
На дошці – портрет вченого і його афоризм:
“Для того, чтобы усовершенствовать ум, надо больше размышлять, чем заучивать”.
Ці слова служитимуть девізом уроку.
Учитель повідомляє тему і мету уроку.
2. Колективна робота під керівництвом учителя.
Побудувати графік нерівності:
![]()
Розв’язання
Спочатку будуємо графік рівняння ![]() , використовуючи алгоритм побудови графіка з двома змінними.
, використовуючи алгоритм побудови графіка з двома змінними.
а) ОДЗ: хєR, yєR
б) Прирівняємо підмодульні вирази до нуля:
х – у = 0, х + у = 0,
у = х; у = -х.
в) Прямі х = у та у = -х розбивають координатну площину на 4 частини, у кожній з яких визначимо знаки першого і другого під модульних виразів.
г) Будуємо графіки в кожній частині площині.
д) Графік рівняння зображаємо пунктирною лінією, бо нерівність строга.
е) Графіком даної нерівності будують усі точки координатної площини, які розташовані всередині чотирикутника.

Учитель пропонує виконати перевірку побудови графіка нерівності за допомогою комп’ютерної програми “Advanced Grapher”.
IV Закріплення вмінь і навичок.
- Самостійна робота.
Побудувати графік нерівностей і виконати перевірку за допомогою комп’ютерної програми “Advanced Grapher”
Варіант 1 ![]()
Варіант 2 ![]()
Варіант 3 ![]()
Варіант 4 ![]()
Учні здають зошити вчителю на перевірку.
V Підбиття підсумку.
Рефлексія.
Використовуючи прийом «Рефлексія», вчитель ставить учням запитання, що стосується не лише вивченого матеріалу, а й такі, що підводять їх до рефлексії: Чи продуктивною була ваша робота на уроці? Чим наповнили свої знання? Чи вдалося вам заповнити прогалини в знаннях?
VI Домашня робота.
№1 Покажіть штриховкою на координатній площині множину точок, координати яких задовольняють системі:
-
а)
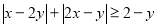
б) 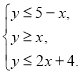
- Знайдіть всі значення параметра а, при яких система рівнянь має єдиний розв’язок.

1


про публікацію авторської розробки
Додати розробку