Урок із теми "Квадратні рівняння"

ТЕМА УРОКУ: КВАДРАТНІ РІВНЯННЯ.

ОСВІТНІ ЦІЛІ: - повторити, узагальнити і систематизувати знання та вміння розв'язувати квадратні рівняння, використовуючи формули коренів квадратних рівнянь; познайомити учнів із життям, творчістю та математичними відкриттями Омара Хайяма; систематизувати набуті знання про розв’язання лінійних та квадратних рівнянь, їх видів .

РОЗВИВАЮЧІ - розвивати вміння узагальнювати та систематизувати;

ЦІЛІ: - коректувати одержані знання;

•    аналізувати й повторювати математичні факти;
•    привчати самостійно мислити, зв’язано висловлювати і правильно оформляти власні думки.

ВИХОВНІ

ЦІЛІ: - виховувати любов до математики, культури математичного

мовлення;

- дотримуватись етичних норм поведінки.

ОБЛАДНАННЯ: підручники, картки з копіркою для виконання самостійної роботи, кольорова крейда, портрет Омара Хайяма; епіграф.

ТИП УРОКУ: урок систематизації та узагальнення знань і навичок .

ХІД УРОКУ

І. ВСТУПНЕ СЛОВО.

Вчитель звертається до учнів: “ О, як я хочу після тисяч років зійти з землі хоч травкою малою”. О. Хайям.

Перенесемося у Стародавній Схід, XI ст.

Звузить вірш:

В Нишапуре базар. Там сутра шум и гам.

Здесь торгует ремесленник - старый Хайям!

Сын пришел помогать - черноглазый Омар.

Звонкий голос летит: "Покупайте товар!”

День окончен. Отец достает кошелек:

“Заслужил ты сегодня подарок, сынок”.

Сын шагает с отцом по базарным рядам.

“Пять дирхемов тебе на подарок я дам.

Ты доволен, Омар? Отвечай, наконец!"

“Дай мне десять динаров ". Споткнулся отец:

“Ты, наверно, забыл, я не шах и не бей!

 

 

Что ты хочешь купить, не пойму, хоть убей!”

Недовольный за сыном плетется старик

На прилавке он видит пять свитков – пять книг.

“Это древний ученый, великий Евклид.

Это - мысль, что любого быстрей скакуна,

Ярче всяких алмазов сверкает она.

Нет без линий и чисел мне жизни, отец!

И узнать я хочу то, что понял мудрец”

Опрокинул в ладони купцу кошелек.

Руки к небу вознес: "Пусть я темен и стар!

Сделай так, чтоб ученым стал сын мой - Омар!”

І Бог почув молитви батька. Його син став не просто вченим, він став творчою особистістю.

И. УСНИЙ ЖУРНАЛ.

Доповідають учні.

Омар Хайям - видатний перський і таджицький вчений та поет (1048-1131р.р.).

Стародавній Схід знав його, передусім, як видатного вченого.

Слава про його дивовижні знання розповсюдилася по всій Середній Азії. Він був видатним математиком, фізиком, філософом - справжнім енциклопедистом свого часу.

“Учений муж століття”, “Доказ істини”, “Знавець грецької науки”,

“Цар філософів Сходу і Заходу” - ось такий далеко не повний перелік почесних титулів Омара Хайяма у зоряні часи його слави.

У 25 років О.Хайям написав свій перший алгебраїчний трактат, що уславив його ім’я як вченого. Він написав серйозні праці з математики та фізики, на основі глибоких астрономічних спостережень створив календар, точніший за сучасний. А ще хвилювали вченого паралельні лінії, ті самі, що стали основою геометрії Евкліда. Чому паралельні лінії ніколи не перетинаються? Чи справді ніколи - навіть у безкрайньому просторі? Сам того не підозрюючи, О.Хайям близько підійшов до вирішення проблеми, яку через багато років після нього розв’яжуть Лобачевский і Ріман.

О.Хайям першим серед математиків створив теорію розв’язування рівнянь до третього степеня включно і дав загальну класифікацію усіх рівнянь у трактаті “Про доведення задач з алгебри”. У цьому трактаті він стверджує, що алгебра - наука про визначення невідомих за допомогою рівнянь. Він також першим поставив питання про зв’язок геометрії з алгеброю і геометричні пояснення у розв’язанні алгебраїчних рівнянь.

 

ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ.

Фронтальна бесіда з класом: “Тепер ми з вами пригадаємо види та розв'язання рівнянь першого і другого ступенів, а розв’язання рівнянь третього ступеня виходить за рамки шкільної програми”.

На дошці контури таблиці. Учні по черзі заповнюють таблицю на дошці, відповідаючи на запитання вчителя.

ЗАПИТАННЯ:

•    Що називається рівнянням?
•    Що називається коренем рівняння?
•    Які рівняння називаються лінійними?
•    Скільки розв’язків може мати лінійне рівняння? Від чого це залежить?

-   Складіть алгоритм розв’язання лінійного рівняння.

 

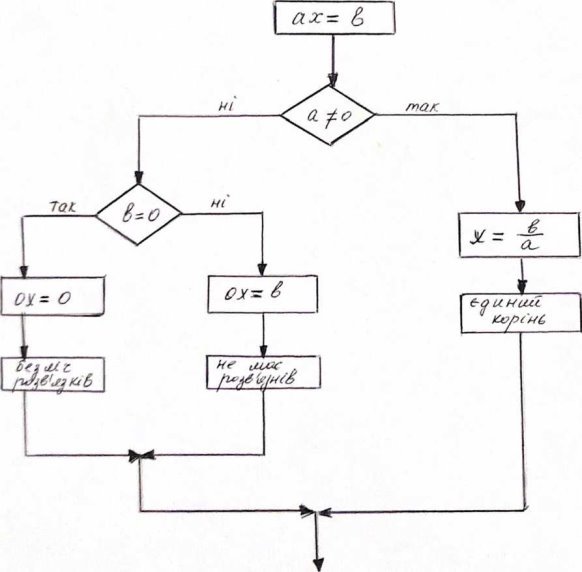
            - Які рівняння називаються квадратними?

•    Чому число а не рівно 0 ?
•    Як називаються числа а,в,с в рівнянні?
•    Які рівняння називаються неповними квадратними?
•    Скільки типів неповних квадратних рівнянь?
•    Записати їх вид.
•    Способи розв'язання неповних квадратних рівнянь.
•    Від чого залежить кількість коренів квадратного рівняння?
•    Як залежить кількість коренів квадратного рівняння від дискримінанта
•    Записати формулу коренів квадратного рівняння.
•   
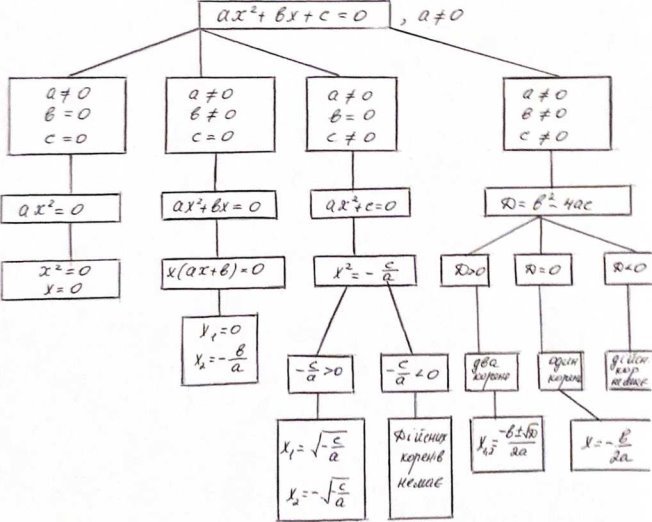
  Записати формулу коренів квадратного рівняння для парного в.

 

ІV. САМОСТІЙНА РОБОТА.

Виконується під копірку. Один примірник здати вчителю. Самоперевірка робіт за зразком на дошці. По закінченні роботи вчитель дізнається у класа, скільки учнів отримали вищий, достатній і середній бали.

1.   ПОЧАТКОВИЙ РІВЕНЬ.

1.    Які з рівнянь є квадратними?

а) 2х + 3 = 0

б) 2х² + 3 = 0

в) 2х² - Зх + 7 = 0

2.     Записати коефіцієнти квадратного рівняння.

5х²+ 9х + 4 = 0

3.     Перевірити чи є число 1 коренем квадратного рівняння? х² - 2х +1=0

2.    СЕРЕДНІЙ РІВЕНЬ.

1.    Розв’яжи рівняння: х² + Зх = 0
2.     Знайди корені квадратного рівняння:

                х² + Зх + 2 = 0

3.     Не розв’язуючи рівняння, встанови, чи має воно розв’язки:

2х² + 6х + 4 = 0

3.    ДОСТАТНІЙ РІВЕНЬ.

1.    Розв’яжи рівняння:

0,7х² = 1,3х + 2

2.     Чи співпадають корені рівняння (можна не розв’язувати):

0,7х² = 1,3х + 2

14x²- 26х - 40 = 0

3.     Скласти рівняння, корені якого протилежні:

0,7х ² = 1,3х + 2

4.    ВИСОКИЙ РІВЕНЬ.

1.    Розв’язати біквадратне рівняння:

z⁴+7z² + 12 = 0

2.     При якому значені параметра с рівняння має один корінь:

7х²-ІЗх + с = 0

3.    РОЗВ’ЯЗАННЯ ТВОРЧИХ ЗАВДАНЬ.

Учні поділяються на 6 команд ( 6 рядів колонок). Кожна колонка розв’язує своє рівняння. Результати розв’язків записуються в таблицю.

Рівняння	Х1	Х2
2)С+5х+2=0	-2	-1/2
3хг-10х+3=0	3	1/3

4х 2+17х+4=0	-4	-1/4
5х2-26х+5=0	5	1/5
6х‘+37х+6=0	-6	-1/6
7х2-50х+7=0	7	1/7

 

ПИТАННЯ ВЧИТЕЛЯ:

•    Яку закономірність ви помітили в загальному вигляді рівнянь?
•    Що можна сказати про коефіцієнти рівнянь?
•    Чим відрізняються ці рівняння?
•    Розв'яжіть рівняння .
•    Якими числами є розв’язки цих рівнянь?
•    Як залежить знак коренів від коефіцієнтів квадратного рівняння?
•    Спробуйте перевірити ці розв’язки за теоремою Вієта.
•    Що спочатку треба зробити з цими рівняннями?
•    Давайте спробуємо скласти загальний вигляд цих рівнянь.
•    Що сказали ми про коефіцієнти а та сі Вони рівні. Отже

ах² +... + а = 0

•    Як залежить коефіцієнт в від коефіцієнта а чи с.?

в = а ‘ + 1, отже ах ²+ ( а² + 1 )х + а = 0

•    Як можна виразити в загальному вигляді корені цього рівняння?

х і= а; х₂= 1/а, або х і = -а; х₂ = -1/а

•    Коли обидва корені додатні?
•    Коли обидва корені від’ємні?
•    Спробуємо довести це в загальному вигляді.
  
  
   

                                                 ДОВЕДЕННЯ

•   

4.    ДОМАШНЄ ЗАВДАННЯ.

1.   Довести цю закономірність для рівняння ах² - (а ²+ 1 )х + а = 0
2.    Розв’язати біквадратне рівняння х⁴ - 10х² + 24 = 0
3.    Розв’язати ірраціональне рівняння х - √x - 6 =96
4.    При якому значені параметру с рівняння має один корінь 7х² - 1Зх + с = 0

5.          ПІДВЕДЕННЯ ПІДСУМКІВ.

О.Хайям залишив по собі величезну кількість наукових трактатів і досліджень, та все ж у сучасному світі його знають більше як поета, аніж як вченого. Його дивовижні чотиривірші (рубаї) й досі захоплюють читачів. Давайте послухаємо, як звучать перлини його творчості:

Чтоб мудро жизнь прожить, знать надобно немало:

Два важных правила запомни для начала:

Ты лучше голодай, чем что попало есть,

И лучше будь один, чем рядом с кем попало.

Не смотри, что иной выше всех по уму,

А смотри, верен слову ли он своему:

Если слов он своих не бросает на ветер - Нет цены, как ты сам понимаешь, ему.