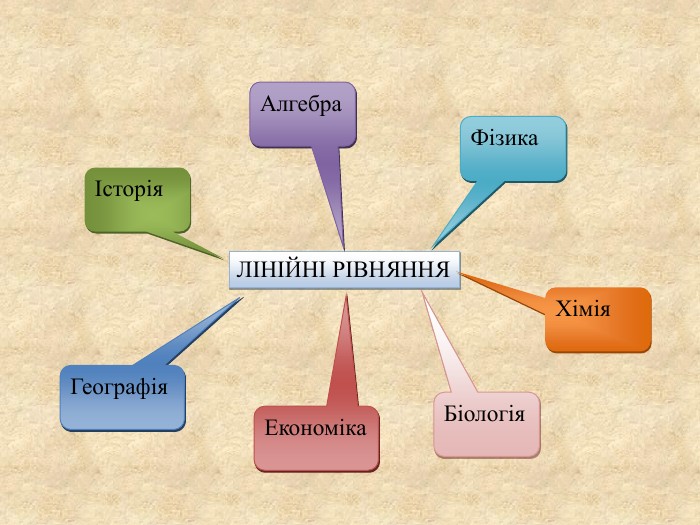
Урок-кейс "Лінійні рівняння"

УРОК-КЕЙС «ЛІНІЙНІ РІВНЯННЯ»

Розгортка за предметами:Історія. ЛІНІЙНІ РІВНЯННЯАлгебра. Фізика. Хімія. Біологія. Економіка. Географія

Історія. Мистецтво розв’язувати рівняння зародилося ще у ті стародавні часи, коли мудреці почали замислюватися про рівності, які містили невідомі величини і називали їх купами, горщиками, корзинами і т. і. Джерела, що до нас дійшли, свідчать про те, що стародавні вчені володіли якимись загальними прийомами розв’язання задач з невідомими. Однак у жодному папірусі на жодній цегляній табличці не надано опису цих прийомів. Виключенням є «Арифметика» грецького математика Діофанта Олександрійського (ІІІ ст.) – збірка задач на складання рівнянь із систематичним викладенням їх розв’язку.

У той же час, першим посібником що до розв’язання задач за допомогою рівнянь стала праця багдадського вченого IX сторіччя Мухаммеда бен Муси аль-Хорезмі. Слово «алгебра» виникло після появи його трактату "Кітаб аль-джебр валь-мукабала", що означає «Книга про відновлення та зіставлення». Термін «аль-джебр», який взято з назви трактату, у подальшому почали вживати, як «алгебра». Відновленням («аль-джебр») Хорезмі називав операцію виключення з обох частин рівняння членів, що віднімаються, шляхом додавання протилежних за знаком. Зіставлення («аль-мукабала») - це взаємознищення в обох частинах рівняння однакових членів. Хорезмі одним з перших почав використовувати рівняння так, як торговець використовує ваги важелів.

У творі аль-Хорезмі невідомі величини, так як і усі супутні викладки та перетворення рівнянь, виражалися словесно. А от традицією позначувати невідомі величини останніми літерами латинського алфавіту (х, у або z) ми зобов’язані співвітчизнику Вієта – Рене Декарту. У 1557 році уельський лікар і математик Роберт Рекорд запропонував використовувати у математиці знак рівності, пояснивши, що ніщо не може бути більш рівним, ніж два паралельних відрізка. Великий прорив у алгебрі пов’язаний з ім’ям французького вченого XVI ст. Франсуа Вієта. Він першим з математиків ввів літерне позначення для коефіцієнтів рівняння та невідомих величин. Винахід Вієта дозволив дуже легко знаходити загальні рішення для схожих задач.

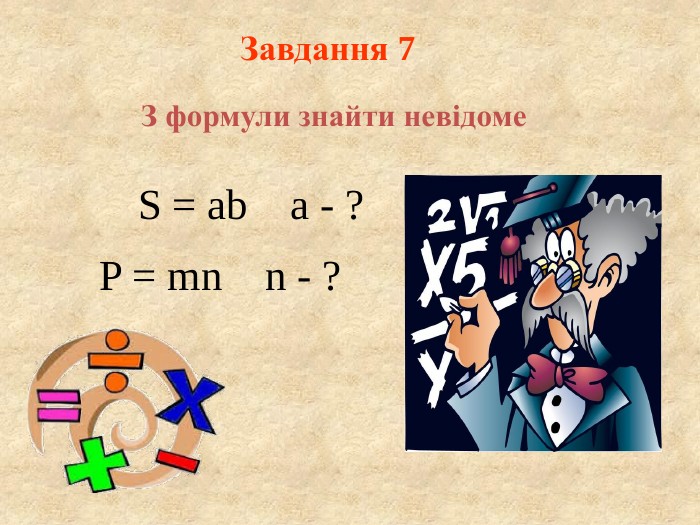
Мета уроку: Розкрити технологію розв’язування текстових задач як математичної моделі. Скласти алгоритм розв’язання задач за допомогою лінійних рівнянь. Відпрацьовувати навички складання лінійних рівнянь за текстом задачі. Тема уроку: Розв'язання задач за допомогою лінійних рівнянь. Рівняння як математична модель задачі.

Рівняння – це ...рівність, яка містить змінну.2х+5=88х-12=3256х=89style.colorfillcolorfill.type

знайти його кореніабодовести, що їх не існує. Розв’язати рівняння – це ...style.colorfillcolorfill.type

значення змінної, при підстановці якої, рівняння перетворюється на вірну числову рівність. Корінь рівняння – це ...style.colorfillcolorfill.type

рівняння, у яких співпадає множина їх коренів. Рівносильні рівняння - це ...style.colorfillcolorfill.type

ОДЗ рівняння...множина значень змінної, при якій обидві частини рівняння мають сенс.style.colorfillcolorfill.type

Лінійне рівняння – це …рівняння вигляду ах = b,де а, b – числа; х - невідомеstyle.colorfillcolorfill.type

Кількість коренів Один корінь х = b/a, якщо а  0 і b  0 Безліч коренів 0х = 0, якщо а = 0 і b = 0 Немає коренів 0х = b, якщо а = 0 і b  0style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

11n = n3|a – 3| = 79х - х3у  823 = 82 x + 5 = 8 - 3x. Завдання 1 Знайти рівняння. Усна роботаstyle.colorfillcolorfill.type

Завдання 2x2 – 5 = 2x + 10 {-3}Доведіть, що дане числоє коренем рівнянняstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Завдання 3|х| = 3|х| = -253|х| = 0x2 = 6 х2 = -96 x2 = 0 х(х - 5) = 0 5х(х - 5)(9 - х)(45х + 7) = 0 8х = 72 + 3х. Скільки коренів має рівнянняstyle.colorfillcolorfill.type

Завдання 4х + 4 = х - 3x2 + 1 = 0 Доведіть, що рівняння немає раціональних коренівstyle.colorfillcolorfill.type

Завдання 5{5}Скласти лінійне рівняння з коренемstyle.colorfillcolorfill.type

Завдання 6|7х| = 142(|х| + 2,6)(х - 5) = 0|0,5-х| = 0 Розв’язати рівнянняstyle.colorfillcolorfill.type

Завдання 7 S = ab a - ?P = mn n - ?З формули знайти невідомеstyle.colorfillcolorfill.type

Завдання 8ax = 15 x = 1/3a - ?Знайти параметр а з лінійного рівняння, якщо задано його коріньstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Завдання 9(a - 2)x + 2 = a. Безліч кореніва - ?При якому параметрі а рівняння має безліч коренів?style.colorfillcolorfill.type

Завдання 10 Складіть рівняння, рівносильне даному, з цілими коефіцієнтами-3,17х = 2,1style.colorfillcolorfill.type

Алгоритм розв’язання задач за допомогою рівнянь. Уважно прочитати задачу. Визначити відомі та невідомі величини. Перевірити відповідність одиниць виміру. Одну невідому позначити за х, а інші виразити через х. Скласти рівняння. Розв’язати рівняння. Знайти відповідь на питання.

Зразок розв’язку задачіЗадача 1. Учень задумав число. Якщо від нього відняти 7, і результат поділити на 3, то дістанемо 5. Яке число задумав учень?Після того, як цю різницю поділити на 3, отримаємо. Отже можна скласти рівняння: Позбавимось знаменниках – 7 = 15;х = 15 + 7;х = 22. Відповідь: Учень задумав число 22. Розв’язання. Нехай учень задумав число х. Якщо від цього числа відняти 7,то отримаємо х – 7. Отримаємоstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Розв’язання задач за допомогою рівнянь. Задача 1 У кошику було в 2 рази менше яблук, ніж у ящику. Після того, як з кошика переклали в ящик 10 яблук, у ящику їх стало в 5 разів більше, ніж у кошику. Скільки яблук було в кошику?Задача 2 В одній касі кінотеатру продали на 86 квитків більше, ніж в другій. Скільки квитків продали в 1-й касі, якщо всього було продано 792 квитка?Задача 3 Периметр трикутника дорівнює 16 см. Дві його сторони рівні між собою і кожна з них на 2,9 см більше третьої. Знайдіть третю сторону трикутника?Задача 4 Сашко, Сергій і Олена разом зібрали в лісі 123 гриба. Сашко зібрав у 2 рази менше грибів, ніж Олена, але на 21 гриб більше, ніж Сергій. Скільки грибів зібрав Сашко?Задача 5 На вантажну машину завантажили в 5 разів більше вантажу, ніж на причіп. Скільки кг завантажили на причіп, якщо на ньому було на 148 кг менше, ніж на машині?

Задача 6 Один кг цукерок дорожче 1 кг печива на 2,6 грн. За 8 кг цукерок заплатили стільки, скільки за 12 кг печива. Скільки коштує 1 кг цукерок?Задача 7 Купили 14 листівок по 16 коп. і по 23 коп., заплативши всього 2 грн. 66 коп. Скільки купили листівок по 23 коп.?Задача 8 За три дні турист пройшов 128 км, причому за другий день він пройшов 3/7 відстані, пройденого за 1-й день, а за третій - 40% тої відстані, що за перший. Скільки км пройшов турист у перший день?Задача 9 В одній шафі було в 4 рази менше книг, ніж у другій. Коли в першу шафу поклали 17 книг, а з другої взяли 25 книг, то в обох шафах книг стало порівну. Скільки книг було в першій шафі спочатку?Задача 10 Човен плив за течією 3,4 год, а проти течії 4 год. Шлях, пройдений човном за течією, виявився на 4,4 км менше шляху, пройденого нею проти течії. Знайти швидкість човна в стоячій воді, якщо швидкість течії ріки становить 2 км/год.

Історія. ЛІНІЙНІ РІВНЯННЯАлгебра. Фізика. Хімія. Біологія. Економіка. Географія

ФІЗИКА

S=Vt. Знаходження переміщення, швидкості, часу

Рівномірний рух – це…Рівномірний рух – це рух із постійною швидкістю.рух, при якому тіло за однакові проміжки часу проходить однакові відрізки шляху.style.colorfillcolorfill.typestyle.colorfillcolorfill.type

Закон Архімеда

FA = ρVg. Закон Архімеда. На будь-яке тіло, занурене у рідину (газ), діє зі сторони цієї рідини (газу) виштовхуючи сила, яка дорівнює добутку густини рідини (газу), об’єму зануреної частини тіла та прискорення вільного падіння.style.colorfillcolorfill.type

Закон Гука

Закон Гука. Сила пружності, що виникає в тілі при пружних деформаціях, прямопропорційна подовженню або стисненню і направлена у протилежний бік руху частинок тіла при деформації.x – деформація, м;k – коефіцієнт жорсткості, н/м.

Закон Шарля

Закон Шарля. Для газу даної маси відношення тиску газу до температури є постійною величиною, якщо об’єм газу не змінюється.style.colorfillcolorfill.type

ТИСКВеличина, що дорівнює відношенню сили, яка діє перпендикулярно на поверхню, до площі цієї поверхні.style.colorfillcolorfill.type

ГІДРОСТАТИЧНИЙ ТИСКР – тиск рідини (газу) на глибині hρ – густина рідини (газу)g – прискорення вільного падінняh – глибина, на якій визначається тиск.hstyle.colorfillcolorfill.type

ХІМІЯ

2 Mg + O2 = 2 Mg. OH2 + Cl2 = 2 HCl2 Al + 3 O2 = 2 Al2 O3 Хімічним рівнянням називають умовний запис хімічної реакції за допомогою хімічних знаків та формулstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

БІОЛОГІЯ

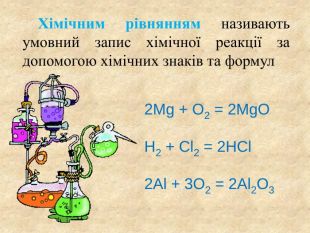
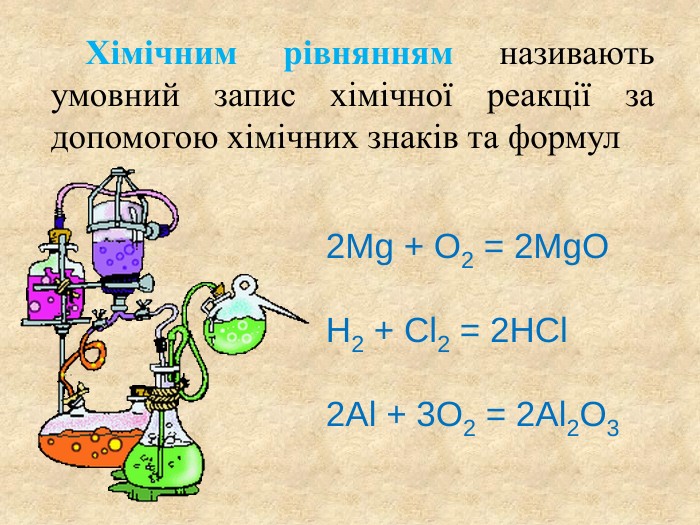
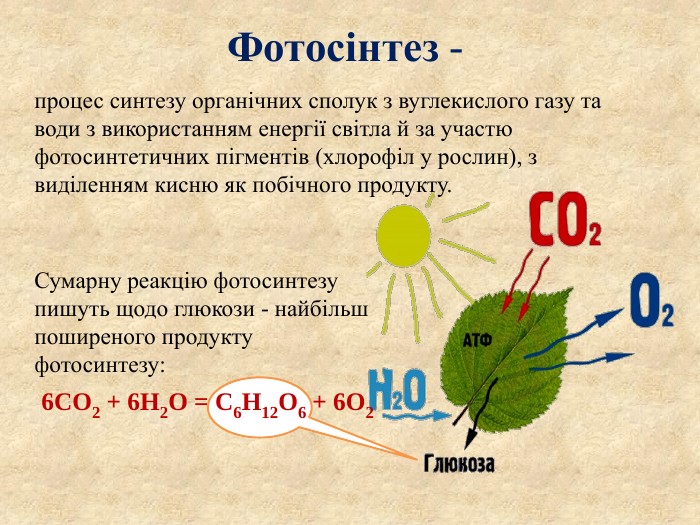
Сумарну реакцію фотосинтезу пишуть щодо глюкози - найбільш поширеного продукту фотосинтезу:6 CO2 + 6 H2 O = C6 H12 O6 + 6 O2 процес синтезу органічних сполук з вуглекислого газу та води з використанням енергії світла й за участю фотосинтетичних пігментів (хлорофіл у рослин), з виділенням кисню як побічного продукту. Фотосінтез -style.colorfillcolorfill.typestyle.colorfillcolorfill.type

ЕКОНОМІКА

ЕКОНОМІКАРівняння сукупного доходу в економіці держави. Y=YC +Yg +YG +N+A= ВНПYC - доходи домогосподарств;Yg - доходи бізнесу;YG - доходи державного сектора економіки;N - непрямі податки на бізнес;A - амортизаційні відрахування на відновлення капіталу в економіці;ВНП - валовий національний продукт. Рівняння сукупних витрат в економіці держави. R=C+Ig +G+Xn =ВНПC - витрати на споживання домогосподарств;Ig - валові приватні внутрішні інвестиції;G - державні закупівлі товарів та послуг;Xn - чистий експорт, або різниця між експортом і імпортом продукції;ВНП - валовий національний продукт. Y= R= ВНП

ГЕОГРАФІЯ

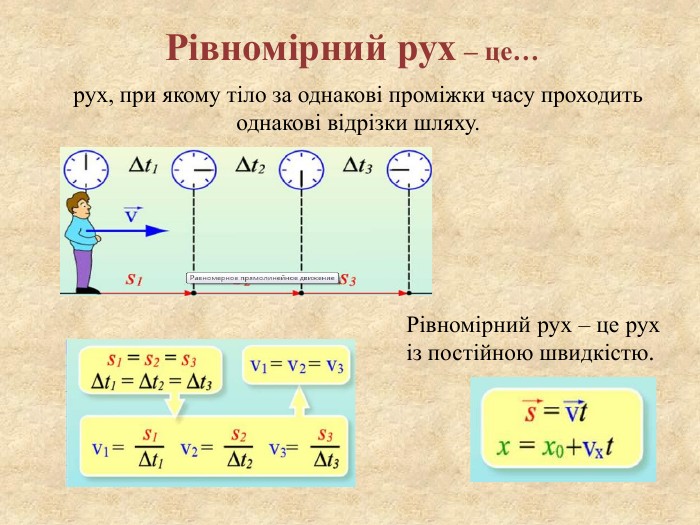
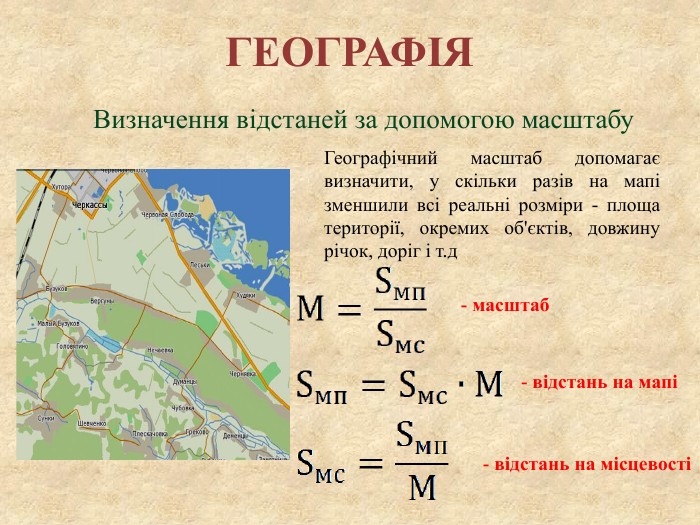
ГЕОГРАФІЯВизначення відстаней за допомогою масштабу. Географічний масштаб допомагає визначити, у скільки разів на мапі зменшили всі реальні розміри - площа території, окремих об'єктів, довжину річок, доріг і т.д- масштаб- відстань на мапі- відстань на місцевостіstyle.colorfillcolorfill.type

ГЕОГРАФІЯЗнаходження висоти полуденного Сонця над горизонтом для різних широтa - кут падіння сонячних променівj - географічна широта. Сонце на екваторіСонце на широті 23,50 півн. ш. Сонце на широті 23,50 півд. ш.style.colorfillcolorfill.typestyle.colorfillcolorfill.type

ГЕОГРАФІЯВизначення коефіцієнту зволоження повітря, кількості опадів, випаровуваностіГеографічне поширення опадів по земній поверхні залежить від сукупної дії багатьох чинників: температури, випаровування, вологості повітря, хмарності, атмосферного тиску, пануючих вітрів. О = В × КЯкщо відомі випаровуваність і  коефіцієнт зволоження, то кількість опадів визначається за формулою:style.colorfillcolorfill.type