Тема : Властивості тригонометричних функцій. Розв’язування вправ.

Мета: 

Формування компетентностей:

•         предметна компетентність: повторити навчальний матеріал із теми: «Тригонометричні функції та їх властивості»; відтворити вміння розв’язувати задачі із цієї теми; 

ключові компетентності:

•         спілкування державною мовою – грамотно висловлюватися рідною мовою, чітко, лаконічно та зрозуміло висловлювати свою думку;

•         інформаційно-цифрова компетентність – діяти за алгоритмом та складати алгоритми;

•         практична компетентність - будувати і досліджувати найпростіші математичні моделі реальних об’єктів, процесів і явищ, задач, пов’язаних із ними, за допомогою математичних об’єктів, відповідних математичних задач;

•         Основні компетентності у природничих науках і технологіях- будувати та досліджувати математичні моделі природних явищ і процесів;  

•         уміння вчитися впродовж життя – визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети;

•         ініціативність і підприємливість – генерувати нові ідеї, аргументувати свою позицію.

Тип заняття : узагальнення й систематизація знань. Заняття-кейс.

Обладнання та наочність: підручник, презентація до заняття, набір карток «Тригонометричне доміно», роздавальний матеріал.

Міжпредметні зв’язки: фізика, інформатика, біологія, музика, астрономія, фізичне виховання.

Використана література:  1. Математика : алгебра і початки аналізу та геометрія, рівень стандарту : підруч. 

для 10 кл. закладів загальної середньої освіти / Г.П. Бевз, В.Г. Бевз. – К.: Видавничий дім «Освіта», 2018. – 288 с. : іл. Режим доступу:

https://lib.imzo.gov.ua/handle/123456789/128 2. Математика : алгебра і початки аналізу та геометрія, рівень стандарту : підруч.  для 10 кл. закладів загальної середньої освіти / А.Г. Мерзляк,  Д. А. Номіровський, В.Б. Полонський , М. С. Якір. – Х.: Гімназія, 2018. – 256.с. : іл.:

https://lib.imzo.gov.ua/handle/123456789/145

Хід заняття

І. Організаційний етап

Перевірка присутніх, налаштування на роботу на занятті

З метою налаштування групи на роботу на проектор на 1-2 хвилини виводиться (слайд 1) Презентації до заняття. Після цього студенти відповідають на запитання (слайд 2)

Пояснення щодо заповнення картки самооцінювання (слайд 3)

       

 

                 

Протягом заняття заповнюємо лист самооцінки ( див. ДОДАТОК А), Кількість балів, які можна отримати за кожне завдання  та шкала  набраних балів в оцінку є у виданому листі самооцінки .

 

ІІ. Перевірка домашнього завдання

      Слайди ( 4-6) презентації                                        

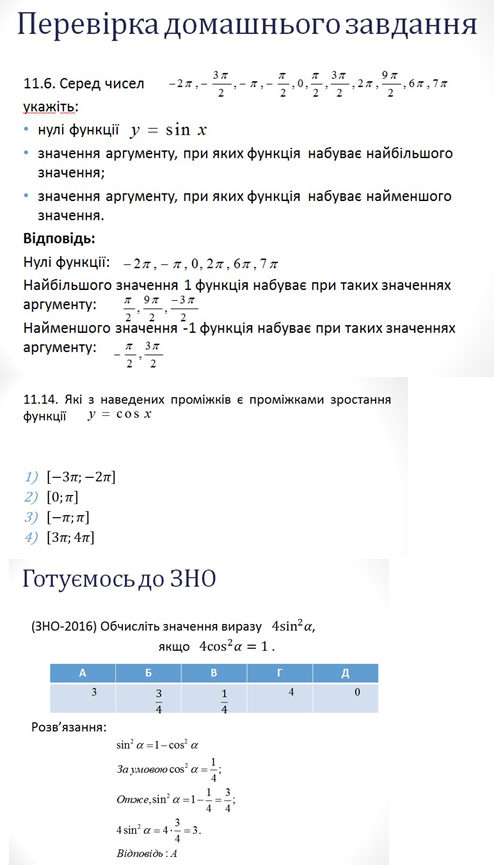
Творчі завдання ( міні-проекти) перевірятимуться під час заняття (слайд 7)

1.        Дослідити  рух Сонця по небесній сфері та описати залежність моменту заходу Сонця від дати на календарі. Описати основні властивості утвореної функції.

2.        (Реалізація наскрізної лінії ключових компетентностей: "Екологічна безпека та сталий розвиток")

                      №      508      [1]      Великої      шкоди      сільськогосподарським       культурам

( виноградникам, плодовим деревам, зерновим тощо) завдають коники, що нерідко

розмножуються     до      господарсько       відчутної чисельності. Для убезпечення посівів еколог протягом t тижнів0 t         12, досліджував популяцію коників і встановив, що зміну їх чисельності наближено можна характеризувати формулою

K t( )  7500 3000     sin^t . Установіть, протягом якого 8

тижня чисельність коників сягала: 1) 6000;   2) 9000.

Якою була найбільша і найменша чисельність коників протягом досліджуваного періоду? Можете скористатися ІКТ.

3.        Розглянути поняття періоду біологічного ритму. Дослідити власний біологічний ритм за допомогою прикладних програм.

ІІІ Повідомлення теми, мети, завдань заняття, мотивація навчальної діяльності

Слайд 8

Перегляньте слова в хмарі. Деякі з них, на перший погляд, не  зовсім відповідають поняттям з розділу тригонометричних функцій.

Розібратися з цим нам допоможе епіграф заняття, який закодовано у вигляді QR- коду . За допомогою ваших мобільних пристроїв розкодуйте епіграф і поясніть, як на вашу думку пов’язані слова в хмарі.

Завдання на занятті:

 – розглянути практичний аспект застосування тригонометричних функцій в різних сферах діяльності людини;

- Навчитися застосовувати прикладні онлайн-сервіси для розв’язування деяких тригонометричних задач, зокрема до побудови графіків тригонометричних функцій.

 

Епіграф  заняття у вигляді qr- коду  ( слайди 8 – 9)                «…Математика безмежно різноманітна як світ, і присутня, міститься в усьому.»         М. П. Єругін.

                  

 

Сьогодні на занятті ми побуваємо в чарівному світі гармонії і краси – у світі властивостей тригонометричних функцій. Намагатимемось показати, що ми всі живемо за їх властивостями, нас оточує багато речей, які підвладні цим законам.

       

ІV. Актуалізація опорних знань 

 

1)                Фронтальне опитування проводиться за методом «Математичне доміно».

 ( див. Додаток Б).( слайд 12) 

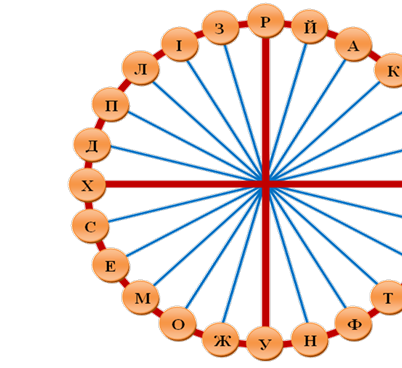
2)                Користуючись малюнком кола з центром у початку координат,

зобразити кути та вписати відповідні букви  у клітинки.( слайд 13)

600	900	-300	-900	2250	-1500	-750	-4500
А	Р	Г	У	М	Е	Н	Т

 

Що означає закодоване слово ?

3)                Записати правильну послідовність дій: Як спростити вираз cos( )ctg ?

А   Виразити ctg_ через sin_ і cos_.

                                       Б Виконати перетворення cos( )  cos_.

                                           В Виконати перетворення cos(  )   cos     .

cos²

Г   Записати відповідь:     . sin

Д   Записати відповідь: cos^2 . sin Е   Записати відповідь: sin_.

Є   Записати відповідь: sin_.

4)                Інтерактивна вправа «Розпізнай графік». (слайди 15-23)

 

                                      

 

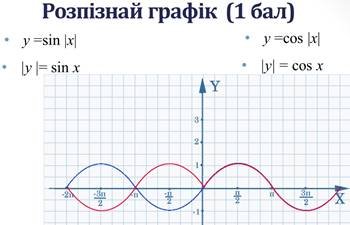
5)                Самостійна робота з подальшою взаємоперевіркою ( слайди 24-25)

 

 

V. Творче застосування узагальнених вмінь та навичок.

Розглянемо, як застосовується тригонометрія в різних сферах життя людини та в природі ( візуалізація руху точки по одиничному колу слайди 26-27)

1.     Технічний аспект застосування ( слайди 24-30) 

Сейсмограф – це прилад, призначений записувати коливання земної кори. Перший сейсмограф, згадка про яке залишилося в історії, був створений в Китаї майже дві тисячі років тому. Строго кажучи, кожен з нас може сам виготовити найпростіший сейсмограф. Для цього потрібно підвісити гирю з загостреним кінцем точно над рівною поверхнею. Будь-яке коливання ґрунту змусить гирю коливатися. Якщо припудрити майданчик під вантажем порошком крейди або борошном, то прокреслені гострим кінцем гирьки смужки вкажуть силу і напрямок коливань.

Осцилограф – пристрій предназначений для дослідження амплітудних і часових параметрів електричного сигналу.

Кардіограф – медичний пристрій, який вимірює біоелектричну активність серця.

Коливання- найпоширеніша форма руху в навколишньому світі та техніці. Коливається дерева, хвилі під дією вітру, поршні у двигуні автомобіля, тощо. Прикладами простих коливальних систем є вантаж на пружині або маятник. Коливання при яких змінення фізичних величин відбувається за законами синуса або косинуса називаються гармонічними.

Розглянемо приклади застосувань описаних явищ ( слайди 28-31) 

Що у фізиці змінюється по синусоїдальному закону?

1.                     Змінний струм синусоїдальний, тобто сила струму в кожній ділянці ланцюга змінюється по синусоїдальному закону І=І0sin(wt+µ), де  І0 – амплітуда струму  w – циклічна частота  µ - початкова фаза.

2.                     ЕРС   (електрорушійна сила) ланцюга      також          змінюється по

синусоїдальному закону

Значення синусоїдних коливань в літаку

При русі літака потрібно стежити, щоб частота синусоїдних коливань літака, спричинена роботою мотора,  не збігались з частотою якою-небудь деталі літака.

До чого може призвести збігання синусоїд?

Резонанс синусоїдних  коливань літака може призвести до аварії.

Висновок.

Досить часто у технічних приладах використовують графік функції синус.

Задача: Усно.(слайд 32)Графік зміни сили струму, що проходить в обмотках котушки блока живлення ноутбука,, описується функцією ysinx1. Знайдіть множину значень сили струму.

Відповідь: E y( ):[0;2]

Задача: (Слайд 33) Траєкторія руху автомобіліста описується функцією y tgx,^_  ^{ }₂ x ₂ ^_, а траєкторія руху велосипедиста – рівнянням y5 . Чи

перетнуться ці траєкторії? Якщо так, то скільки разів?

Відповідь: Траєкторії перетнуться 1 раз.

 

 

2.     Тригонометрія в астрономії (слайд 34)

Необхідність у розв’язанні трикутників раніше за все виникла в астрономії. Тому протягом довгого часу тригонометрія вивчалася і розвивалася як один з розділів астрономії.

Захід сонця – магічний час, який заворожує художників, фотографів, виробників листівок та закоханих. Розглянемо чим же зацікавив захід сонця майбутніх програмістів. Та як захід сонця пов’язаний з тригонометричними функціями.

Творче завдання 1( виступ студента)

3.     Тригонометрія в природі (слайд 35)

Рухи  у тваринному світі відбуваються за законом синуса. Крила птахів, хвости китів, тіло зміїї рухаючись, відтворюють графік синусоїди. 

Творче завдання 2( виступ студента)

Творче завдання 3( виступ студента)

4.     Тригонометрія в музиці (слайд 36)

Гармонічні коливання можна спостерігати слухаючи музику, адже при цьому в повітрі утворюються звукові хвилі, близькі до синусоїди.

5.     Тригонометрія в спорті ( слайд 37)

Рухи стопи бігуна по твердій поверхні відтворюють графік функції y sin x .

Задача 3  (Слайд 38-39) Маршрут туристів має форму косинусоїди. Якою функцією треба описати цей маршрут, щоб він пройшов через точку (;2)?

Відповідь : ycosx1

6.     Тригонометрія в мистецтві і архітектурі ( слайд 37-41)

Для того щоб створити такі елегантні форми архітекторам та інженерам крім опору матеріалів, матеріалознавства та інших прикладних дисциплін треба знайти ще й тригонометрію.

Завдання: графіки яких тригонометричних функцій використовували архітектори у розрахунках об’єктів, зображених на фотографіях?

 

VІ. Підсумок заняття. Рефлексія

Усюди в нашому житті ми зустрічаємось з коливальними рухами, починаючи від коливань маятника, ресора, струсів кузова автомобіля, чи вагона потяга до страшних, руйнівних коливань кори нашої планети; заводські труби і високі будівлі коливаються від вітру подібно до полотна ножівки, затисненого одним кінцем в лещатах. Правда, ці коливання не такі вже й великі. Амплітуда коливань Ейфелевої вежі у Парижі (300м висота) при сильному вітрі приблизно 50см.

Також можна спостерігати хвильові процеси: хвилі на морі, на хлібній ниві. І все це відбуваєтсья за законом синусоїди.

Сьогодні на занятті ми розглянули не лише практичні аспекти застосування тригонометрії, а й навчилися на прикладі творчих завдань розв’язувати задачі за допомогою прикладних програм. В майбутньому, ви як програмісти зможете самі створювати такі програмні  продукти. Але для цього треба наполегливо вчитися.

Я бажаю Вам, щоб ваші знання завжди нагадували тангенсоїду!

 

 

VІІ. Домашнє завдання Повторити матеріал розділу Розв’язати задачі:

1.     На змаганнях з фрістайлу траєкторія руху спортсмена описується функцією

ycosx, а траєкторія руху знімальної камери – рівнянням x_^. Чи 4 перетне оператор лижню спортсмена? Якщо так, то скільки разів?

2.     Басейн наповнювали водою протягом деякого часу. Спостерігач, застосовуючи індивідуальну методику вимірювань наповненості басейна записав такі вирази: sin^{  };sin ;sin ;sin3 ;sin15^{0 0}. Проте вони розміщені в

                                                                                                   4        3        2

хаотичному порядку. Відновіть порядок  запису.

3.     11. 5. [2] стор. 70

Чи проходить графік функції ysin xчерез точку:

1)      A4 ;1 ; 2) B; 1 ;  3) C 236; 12. 

4.     11.8. [2] стор. 70

                              Які з чисел 3, , ^{ },0,      ,      , ⁵,3:

                                                                    2               2         3 2 2

1)      є нулями функції y tgx;

2)      не належить області визначення функції y tgx?

       

ДОДАТОК А

       

Дата _______________  _______ Картка  самооцінки  студента   --------------------------------------------------------
	Вид роботи	Max бал	Бал с/о
	«Тригонометричне доміно»	1 бал
	Гра «Розкодуйте слово	2 бали
	Послідовність дій буквами	1 бал
	Інтерактивна вправа: «Розпізнай графік»	9 балів (по 1 балу за кожен)
	Побудова графіка самостійно	4 бали
	Задача1	1 бал
	Задача2	1 бал
	Задача3	2 бали
	Додаткові бали
Оцінка  :
Норми оцінювання: •              19-20 балів  і більше  - оцінка «11»; •              17-18 балів - оцінка «10»; •              15-16 балів - оцінка «9»; •              13 - 14   балів -  оцінка «8»; •              10- 12 балів - оцінка «7»; •              7 - 9 балів - оцінка «6»; •              5-6 балів - оцінка «5»; •              4-  бали -  оцінка «4»; •              менше 4 балів -  оцінка «3» Примітка: творчі завдання оцінює викладач

ДОДАТОК Б Гра «Тригонометричне доміно»

СТАРТ

Дайте означення синуса числа.

 

Це ордината точки одиничного кола

Вісь тангенсів це

 

Дотична до одиничного кола в точці (1;0)

Найменше значення функції ysinx

 

-1

Дайте означення косинуса числа

 

Це абсциса точки одиничного кола

Найменший додатний період функцій ysinx та ycosxдорівнює …

 

2

Дайте означення тангенса числа

 

Це відношення синуса числа α до його косинуса

Вісь ординат називається віссю …

 

синусів

Дайте означення котангенса числа

 

Це  відношення косинуса числа α до його синуса .

Серед тригонометричних функцій парною є

 

Функція ycosx

Які тригонометричні функції не мають найбільшого та найменшого значень?

 

y ctgx y, tgx

Найбільше значення функції ycosx дорівнює

 

1

Дотична до кола в точці (0;1) називається віссю

 

котангенсів

Графіки функцій y sin x, y tgx

 

Проходять через початок координат

Продовжити формулу sin2

 

2sin cos

Яка тригонометрична функція є зростаючою на всій своїй області визначення?

 

y tgx

Для якого кута з проміжку 0;2  sin x  cosx? 

 4

Основна тригонометрична тотожність :

 

sin2 cos2 1

Найменший додатній період функцій y ctgx y, tgx

 



В якій чверті всі тригонометричні функції додатні?

 

В І чверті

Яка тригонометрична функція є спадною на всій своїй області визначення?

 

y ctgx

Продовжити формулу cos 302  0 sin 302  0  …

 

cos600=

1 радіан це

 

Центральний кут, що спирається на дугу, яка дорівнює радіусу кола

В якій чверті y tgx y, sin xодночасно набувають від’ємних значень?

В ІV чверті.

Чому дорівнює синус 300?

 

Область визначення функцій ysin ,x y cosx

Множина всіх дійсних чисел

Область значень функцій ysin ,x y cosx

 

1;1 відрізок

ФІНІШ