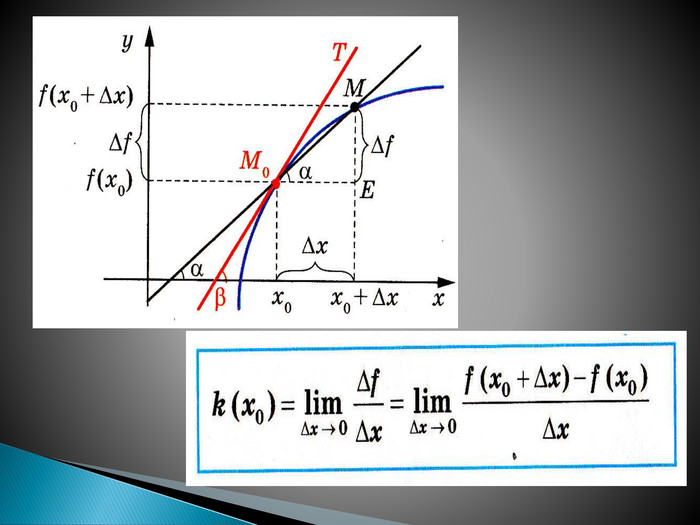
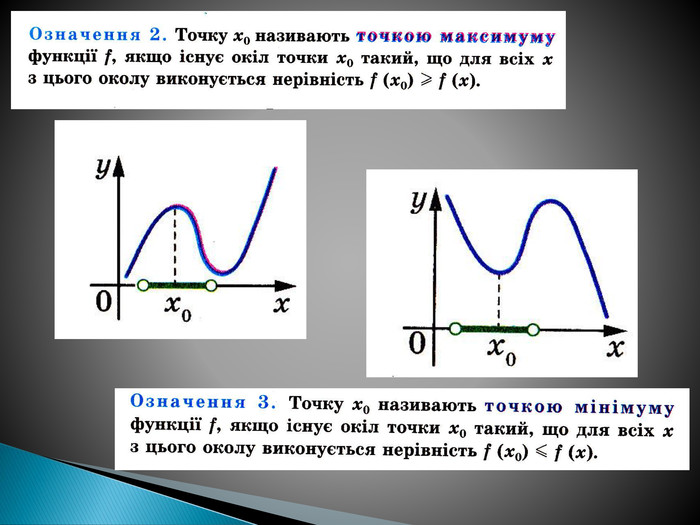
Конспект уроку з алгебри для 10 класу на тему: «Творці диференціального числення»

Творці диференціального числення

 Відкриттю похідної і основ диференціального числення передували роботи математика і юриста П’єра Ферма (1601 – 1665), який у 1629 році запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих, що фактично спиралися на застосування похідних

1-А ГРУПА

1-й учень  Математика завжди була Ферма лише захопленням, і тим не менш він заклав основи багатьох її областей: аналітичної геометрії, числення нескінченно малих і теорії ймовірностей. Ферма не залишив жодної закінченої роботи, і більшість його начерків не було опубліковано при житті.

П’єр Ферма народився на півдні Франції в містечку Бомон-де-Ломань, де його батько — Домінік Ферма — був «другим консулом», тобто чимось на зразок помічника мера. Метричний запис про його хрещенні від 20 серпня 1601 року говорить: «П’єр, син Домініка Ферма, буржуа і другого консула міста Бомону».

У коледжі П’єр придбав хороше знання мов: латинської, грецької, іспанської, італійської. Ферма славився як тонкий знавець античності, до нього зверталися за консультацією з приводу важких місць при виданнях грецьких класиків.

Але Ферма направив всю силу свого генія на математичні дослідження. І все ж математика не стала його професією. Ферма обирає юриспруденцію. Ступінь бакалавра була йому присуджена в Орлеані. З 1630 року Ферма переселяється в Тулузу, де отримує місце радника в Парламенті (тобто суді). У 1631 році Ферма одружився на своїй далекій родичці з материнської сторони — Луїзі де-Лонг. У П’єра і Луїзи було п’ятеро дітей, з яких старший, Самюель, став поетом і вченим. Йому ми зобов’язані першим зібранням творів П’єра Ферма, що вийшов у 1679 році. Жоден з його творів не було опубліковано при житті. Однак кільком трактатам він надав цілком закінчений вигляд, і вони стали відомі . Однією з перших математичних робіт Ферма було відновлення двох загублених книг Аполлонія «Про плоскі місця».

Велику заслугу Ферма перед наукою бачать, звичайно, у введенні їм нескінченно малої величини в аналітичну геометрію. Він зробив цей важливий крок у своїх роботах у 1629 році.

До Ферма систематичні методи обчислення площ розробив італійський вчений Кавальєрі. Але вже в 1642 році Ферма відкрив метод обчислення площ, обмежених будь-якими «параболами» і будь-якими «гіперболами». Їм було показано, що площа необмеженої фігури може бути кінцевою.

Ферма одним із перших зайнявся завданням спрямлення кривих, тобто обчисленням їх довжини дуг. Він зумів звести цю задачу до обчислення деяких площ. Подальший успіх методів визначення «площ», з одного боку, і «методів дотичних і екстремумів» — з іншого, полягав у встановленні взаємозв’язку цих методів.

У задачі другої своєї книги «Арифметики» Діофант поставив завдання подати квадрат раціонального числа у вигляді суми двох раціональних квадратів. На полях проти цієї задачі, Ферма написав: «Навпаки, неможливо розкласти ні куб на два куба, ні біквадрати на два біквадрата і взагалі ні в якому великому степені квадрата, на два степені з тим же показником. Я відкрив  воістину чудове доведення, але ці поля для нього занадто вузькі». Це і є знаменита Велика теорема, яка стоїть на першому місці за кількістю даних її хибних доведень. Сам Ферма залишив доведення Великої теореми для четвертих степенів.

Ферма першим прийшов до ідеї координат і створив аналітичну геометрію. Він займався також завданнями теорії ймовірностей. Ферма належить відкриття закону поширення світла в середовищах. Застосувавши свій метод максимумів і мінімумів, він знайшов шлях світла і встановив, зокрема, закон заломлення світла.

П’єр Ферма помер 12 січня 1665 року під час однієї з ділових поїздок.

2-й учень

3-й учень

 Відкриттю похідної і основ диференціального числення сприяли також праці Рене  Декарта (1596 – 1650), який розробив метод координат і основи аналітичної геометрії.

2-А ГРУПА

1-й учень   Народився Рене Декарт 31 березня 1596 році у французькому місті Лае в сім’ї з дворянським корінням. Рене Декарт після смерті матері виховувався бабусею. Навчався у коледжі Ла Флеш, де отримував релігійну освіту.

 У 1618 році почав вивчати юридичні питання, також займаючись математикою. У 1617 році вступив у голландську армію. Разом з німецькою армією виступав в битві за Прагу. У 1629 році переїхав до Нідерландів.

 Ніщо людське не було чужим для нього — правда, єдиний його любовний роман тривав всього лише три роки. Коханою Декарта була якась голландська жінка, яка в 1635 році народила йому дівчинку. Декарт обожнював дитину і був сильно вражений раптовою смертю дочки у п’ятирічному віці. Він завжди казав про цю втрату як про найбільше нещастя у своєму житті.

 Для продовження занять математикою Декарт повернувся до Парижа, але столичне життя знову швидко набридло йому. Він продав маєток, який отримав від батька і переїхав до самотнього сільського будинку в Голландії. У ті часи багато часу приділяв науці. У 1637 році була надрукована праця Декарта «Міркування про метод». Слідом вийшли роботи: «Роздуми про першу філософію», «Начала філософії».

 Багато років праці Декарта не визнавалися. Декарт захворів на запалення легень і помер 11 лютого 1650 року. У математиці Декарт запровадив Декартову систему координат, дав поняття змінної величини і функції, ввів багато алгебраїчних позначень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. Декарт — автор методу радикального сумніву в філософії, механіцизму у фізиці, передтеча рефлексології. Основні математичні праці Декарта – «Міркування про метод» (у книзі викладені питання аналітичної геометрії), додатки до книги. Також вчений розглядав символіку Вієта, многочлени, рішення алгебраїчних рівнянь, комплексні числа (їх математик називав                    «помилковими»).

2-й учень

3-й учень

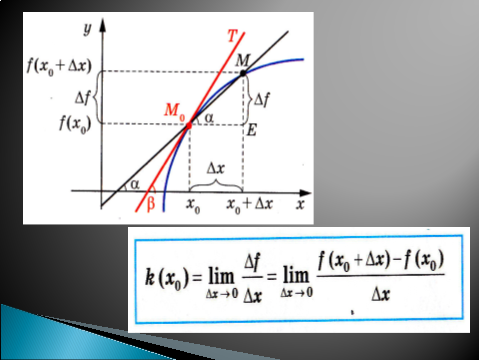
Лише 1666 року Ісаак Ньютон і дещо пізніше Готфрід Лейбніц незалежно один від одного побудували теорію диференціального числення.   І. Ньютон прийшов до поняття похідної, розв’язуючи задачі про миттєву швидкість, а Г. Лейбніц  - розглядаючи геометричну задачу про проведення дотичної до кривої. Ньютон і Лейбніц досліджували проблему максимумів і мінімумів функцій. Зокрема, Лейбніц сформулював теорему про достатню умову зростання і спадання функцій на відрізку.

3-Я ГРУПА

1-й учень  Ісаак Ньютон – великий англійський учений, фізик, математик, алхімік і астроном, який зробив великий внесок у становлення класичної механіки і сучасної фізики. Найбільш відомим відкриттям Ньютона став закон всесвітнього тяжіння. Крім цього він описав всі фізичні явища на основі механіки і пояснив рух планет навколо Сонця і Місяця навколо Землі.

Ісаак Ньютон народився 4 січня 1643 року в містечку Вулсторп в Англії в сім’ї дрібного, але заможного фермера. Отримавши основну шкільну освіту, Ньютон вступив до коледжу Святої Трійці при Кембріджському університеті. Там, під впливом фізиків, він зробив кілька відкриттів, в основному математичних. Також, він почав проводити досліди над розкладанням світла.

 У 1668 році йому було присвоєно ступінь магістра. Через кілька років вінзробив другий дзеркальний телескоп, який був набагато більшим попереднього і ефективнішим. У 1687 році була опублікована його фундаментальна праця «Математичні початки натуральної філософії» або просто «Начала», яка заклала основи не тільки раціональної механіки, але і всього математичного природознавства. У цій праці містилися закон динаміки, всесвітнього тяжіння, додатки про рух небесних тіл, вчення про опір рідин і газів.

У 1705 році Ісааку Ньютону було запропоновано лицарське звання. Так,  правляча в ті часи, королева Анна віддячила великому вченому за його праці. На схилі років, Ньютон проводив багато часу над вивченням теології, античної та біблійної історії.

Ісаак Ньютон помер 30 березня 1727 року і був похований у Вестмінстерському Абатстві – англійському національному пантеоні.

2-й учень

3-й учень

 4-А ГРУПА

1-й учень Готфрід Вільгельм Лейбніц (Gottfried Wilhelm von Leibniz) — провідний німецький філософ, логік, фізик, математик, мовознавець та дипломат. Народився він 1 липня 1646-го року у Лейпцигу (Німеччина), помер 14 листопада 1716 року у Ганновері.

Саме Лейбніц передбачив принципи сучасної комбінаторики. Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Незалежно від Ньютона створив диференціальне й інтегральне числення і заклав основи двійкової системи числення.

У рукописах і листуванні, які було надруковано лише в середині XIX ст., Лейбніц розробив основи теорії детермінантів. Зробив вагомий внесок у логіку і філософію. Мав надзвичайно широке коло наукових кореспондентів. Багато з його ідей викладено в рукописах і листуванні, що ще й досі повністю не надруковані.

У 1661-му році, у віці 14 років, Лейбніц вступив до Лейпцизького університету, де у 1663-му році отримав ступінь бакалавра, з дисертацією “De Principio Individui”, з якої бере початок його пізніша теорія монад.

Викладання математики в Лейпцигу було неякісним. Влітку 1663 р. Лейбніц навчався у Йенському університеті, де на нього мав великий вплив філософ і математик Ерхард Вейгель.

У жовтні 1663 р. Лейбніц повертається до Лейпцига і розпочинає курс навчання на доктора права. Отримує ступінь магістра філософії за дисертацію, яка поєднує аспекти філософії і права з деякими математичними ідеями, що походять від Вейгеля. Отримує ступінь бакалавра права, працює над докторською дисертацією з філософії.

Незважаючи на його неабияку на той час репутацію і визнання його праць, Лейбніцу було відмовлено у ступені доктора права в Лейпцигу, тому він негайно поїхав до Альтдорфа, де у лютому 1667 р. отримав цей ступінь за свою дисертацію “De Casibus Perplexis”. Йому була запропонована посада професора в Альтдорфі, але Лейбніц відмовився, обравши натомість кар’єру дипломата і юриста. У 1667-1672 роках перебував на службі Майнського курфюрста, барона Йоганна Кристіана фон Бойнебурґа, завдяки якому у 1672р. він дістав змогу подорожувати до Парижа, де він залишатиметься до жовтня 1676 р., і до Лондона взимку 1673 р.

Під час цих подорожей Лейбніц познайомився з деякими найвидатнішими вченими і філософами того часу, зокрема Арно, Малебраншем і Гюйгенсом у Парижі, а також Гуком, Бойлем і Пеллем у Лондоні. Під час перебування у Парижі, Лейбніц розпочав дослідження з диференціального й інтегрального числення. Лейбніц надавав надзвичайну увагу питанням зручної наукової нотації, і в рукописі від 21 листопада 1675 р. він уперше використав нині загальновизнаний запис для інтегралу функції. З грудня 1676 р. до кінця свого життя Лейбніц обіймає посади надвірного бібліотекаря та канцлера у місті Ганновер.

Лейбніц листувався майже з усіма тогочасними науковцями Європи, до його кореспондентів належало понад 600 осіб. Він переконав Фрідріха Вільгельма I заснувати Бранденбурзьке наукове товариство (пізніше – Берлінська академія наук) і з 1700-го року був його президентом. На прохання Петра I розробив проекти розвитку освіти і державного управління в Росії. Також доклав чимало зусиль для заснування наукових академій у Санкт-Петербурзі (яку було створено вже після його смерті) та Відні.

Лейбніц шукає можливості для розширення наукових контактів. Він розпочинає листування з Ольденбургом, секретарем Лондонського наукового товариства. Восени 1672 р., з нагоди дипломатичної місії від Бойнебурга у Парижі, Лейбніц обізнається з Гюйгенсом і за його керівництвом розпочинає дослідження з теорії рядів і знаходить славетну формулу.

Під впливом Гюйгенса Лейбніц вивчає праці Паскаля, Грегорі та інших з інфінітезімальної геометрії, тобто питання дотичних до кривих, і виходить з ідеєю “функції”, в сучасній термінології — похідної, таким чином винаходячи центральну концепцію математичного аналізу.

Ньютон написав два листа до Лейбніца, в яких повідомив про свої дослідження з аналізу, але без викладання методів. У відповідь Лейбніц описав деякі зі своїх методів, щодо яких Ньютон зневажливо зауважив: “…не розв’язане жодне попередньо відкрите питання…”.

2-й учень

3-й учень

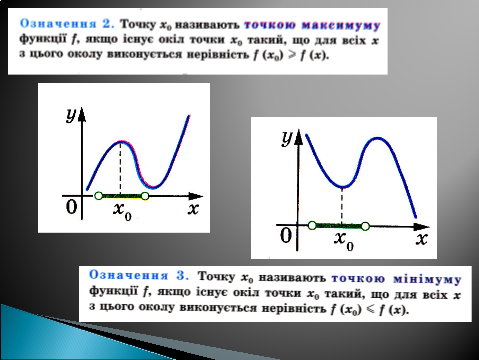
 Леонард Ейлер у праці «Диференціальне числення» (1755 р.) розрізняв локальний екстремум і найбільші та найменші значення функції на певному відрізку. Він перший почав використовувати грецьку букву Δ для позначення приросту аргументу Δх і приросту функції Δу.

5-А ГРУПА

1-й учень  Ейлер вважається найвидатнішим математиком 18-го століття Ейлер народився 15 квітня 1707 р. в м Базель, в Швейцарії. Незабаром після народження сина, родина переїжджає в містечко Рієн. Батько хлопчика був другом Йоганна Бернуллі – відомого європейського математика, що зробив великий вплив на Леонарда. У тринадцять років Ейлер-молодший вступає до Базельського університету, і в 1723 р отримує ступінь магістра філософії. У своїй дисертації Ейлер порівнює філософії Ньютона і Декарта.

 Йоганн Бернуллі, що давав хлопчикові по суботах приватні уроки, швидко розпізнає видатні здібності хлопчика до математики і переконує його залишити ранню теологію і зосередитися на математиці. У 1727 р Ейлер бере участь в конкурсі, організованому Паризькою академією наук, на кращу техніку установки корабельних щогл. Леонард займає друге місце, в той час як перше дістається П’єру Бугеру, який згодом стане відомий як «батько кораблебудування». Ейлер щороку бере участь в цьому конкурсі, отримавши за своє життя дванадцять цих престижних нагород.

 17 травня 1727 р. Ейлер надходить на службу до медичного відділення Імператорської російської академії наук в Санкт – Петербурзі, але майже відразу ж переходить на математичний факультет. Однак через заворушення в Росії, 19 червня 1741 р Ейлер переводиться в Берлінську академію. Там учений прослужить близько 25 років, написавши за цей час понад 380 наукових статей.

 У 1755 р. його обирають іноземним членом Шведської королівської академії наук. На початку 1760-х рр. Ейлеру надходить пропозиція навчати наукам принцесу Ангальт-Дессау, якій вчений напише більше 200 листів, які увійшли популярний збірник «Листи Ейлера на різні предмети натуральної філософії, адресовані німецькій принцесі». Книга не тільки наочно демонструє здатності вченого міркувати на всілякі теми в області математики і фізики, але також є виразом його особистих і релігійних поглядів. Цікаво те, що ця книга відома краще, ніж всі його математичні праці. Причиною такої популярності цих листів стала дивовижна здатність Ейлера в доступній формі доносити наукові відомості до простого обивателя.

Унікальність цієї праці полягала ще й в тому, що в 1735 р. учений майже повністю осліп на праве око, а в 1766 р. ліве око було вражене катарактою. Але, навіть не дивлячись на це, він продовжує свої роботи і в 1755 р. пише в середньому по одній математичній статті в тиждень.

 У 1766 р. Ейлер приймає пропозицію повернутися в Петербурзьку академію, і решту свого життя проведе в Росії. Однак його другий приїзд в цю країну виявляється для нього не таким вдалим: в 1771 р. пожежа знищує його будинок, а, слідом за цим, в 1773 році він втрачає свою дружину Катарину. 18 вересня 1783 року, після сімейного обіду, у Ейлера трапляється крововилив в мозок, після чого, через кілька годин, він помирає. Поховали вченого на Смоленському лютеранському кладовищі на Василівському острові, поруч з його першою дружиною Катариною.

 На згадку про його величезний внесок у науку, портрет Ейлера з’явився на швейцарських 10 – франкових банкнотах шостої серії, а також на ряді російських, швейцарських і німецьких марок.

 Серед всіх різноманітних робіт Ейлера найпомітнішою є уявлення теорії функцій. Він першим ввів позначення f (x) – функції “f” по аргументу “x”. Ейлер також визначив математичні позначення для тригонометричних функцій в тому вигляді , в якому ми знаємо їх зараз , ввів літеру “e” для заснування натурального логарифма (відому як «число Ейлера»), грецьку букву “Σ” для підсумкової суми і букву “і” для визначення уявної одиниці. А               Ейлер затвердив застосування показникової функції і логарифмів в аналітичних доведеннях. Він відкрив спосіб розкладання різних логарифмічних функцій в степеневий ряд, а також успішно довів застосування логарифмів для комплексних числел. Таким чином, Ейлер значно розширив математичне застосування логарифмів. Цей великий математик також докладно пояснив теорію вищих трансцендентних функцій і представив новаторський підхід до вирішення квадратних рівнянь. Він відкрив техніку розрахунку інтегралів із застосуванням складних меж. Розробив він і формулу варіаційного обчислення, що отримала назву «рівняння Ейлера – Лагранжа».

  Ейлер довів малу теорему Ферма, тотожності Ньютона, теорему Ферма про суми двох квадратів, а також значно просунув доведення теореми Лагранжа про суму чотирьох квадратів. Помітний внесок вніс Ейлер в рішення рівняння пучка Ейлера-Бернуллі, яке стало одним з основних рівнянь, застосовуваних в інженерній справі. Свої аналітичні методи вчений застосовував не тільки в класичній механіці, але і в рішенні небесних завдань. За свої досягнення в області астрономії Ейлер отримав численні нагороди Паризької академії. Грунтуючись на знанні істинної природи комет і розрахувавши паралакс Сонця, вчений чітко обчислив орбіти комет та інших небесних тіл. За допомогою цих розрахунків були складені точні таблиці небесних координат.

2-й учень

3-й учень