Урок "Коло і круг. Задачі"

Про матеріал

Розробка уроку із теми "Коло і круг" з прикладами розв'язаних задач прикладного характеру та задачами для самостійного розв'язування

Перегляд файлу

Коло і круг

Завдання: Намалювати лінію без початку і без кінця

Арена цирку, кратер вулкана, спортивний диск, колесо, обруч ... Що спільного у перелічених об'єктів? (їх форма.)

Ми сьогодні будемо говорити на уроці про геометричну фігуру, яку в Давній Греції вважали символом досконалості, козаки сходились на ній, за її кількістю можна підрахувати вік дерева, у цієї фігури немає жодної діагоналі, не можна провести ні бісектриси, ні висоти. Що ж це за фігура?

«Інтелектуальна розминка»

- Дайте відповідь на запитання:

1) відрізок, що з’єднує точку кола з центром (радіус)

2) частина площини, обмежена колом (круг)

3) відрізок, що з’єднує дві точки кола і проходить через центр (діаметр)

4) множина точок, рівновіддалених від однієї (коло)

5) частина круга, що лежить усередині відповідного центрального кута (сектор)

Теоретичні відомості:

Коло — це фігура, що складається з усіх точок площини, рівновіддалених від даної точки (центра кола).

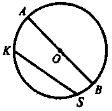
О — центр, КS — хорда, АВ — діаметр, ОА = ОВ — радіус; d = 2R, де R — радіус; d — діаметр.

- Як зміниться довжина кола, якщо радіус кола збільшити у 3 рази?

- Як при цьому зміниться площа круга?

Увага! Чорна скриня!

Те, що лежить в чорній скрині, винайшов талановитий юнак. Під попелом Помпеї археологи знайшли багато таких предметів, виготовлених із бронзи.

В Давній Греції користування цим предметом вважалось верхом досконалості. А вміння розв’язувати задачі з його допомогою – ознакою великого розуму. За сотні років його конструкція не змінилась. В наш час ним вміє користуватись будь-який школяр.

Питання: що лежить в чорній скрині?

Відповідь: циркуль.

Задача 1. Знайдіть довжину обруча радіусом 0,7 м.

А) 1,6 м

Б) 1,4 м

В) 1,8 м

Г) 3,14 м

Задача 2. Обчисліть площу циркової арени діаметром 12 м.

А) 36м²

Б) 64м²

В) 314м²

Г) 49м²

1А; 2Б.

Задача 3. Знайдіть довжину обруча радіусом 0,8 м.

А) 1,6 м

Б) 1,4 м

В) 1,8 м

Г) 3,14 м

Задача 4. Обчисліть площу циркової арени діаметром 14 м.

А) 36м²

Б) 64м²

В) 314м²

Г) 49м²

3 – А; 4 – Г;

Задача 5. Знайдіть довжину обруча радіусом 0,9 м.

А) 31,4 м

Б) 1,4 м

В) 1,8 м

Г) 3,14 м

Д) 1,6 м

Задача 6. Обчисліть площу циркової арени діаметром 16 м.

А) 36м²

Б) 64м²

В) 314м²

Г) 49м²

5 – В; 6 – Б;

Задача 1.

Якщо обтягнути земну кулю по екватору проволокою і потім добавити до її довжини 1 м, то чи зможе в зазор між проволокою і землею проскочити миша?

Розв’язання

Нехай довжина проволоки х м.

Якщо R - радіус Землі, довжина проволоки була С₁ = 2R см, а стане С₂ = 2R + х) см.

За умовою їх різниця дорівнює 1 м або 100 см.

Розв’яжемо рівняння:

2R + х) - 2R = 100,

2R + 2х - 2R = 100,

2х =100,

х = , х 16 см.

Результат свідчить про те, що не тільки миша може проскочити, а й навіть кішка.

Задача 2.

Діаметр опаленої площі тайги від вибуху Тунгуського метеориту дорівнює 38 км. Яка площа тайги постраждала від метеориту?

Розв’язання

Шукану площу знайдемо за формулою S = R².

За умовою d = 38 км, тоді R = 19 км.

Тоді S = 3,14∙ 19² = 3.14∙ 361 = 1133,54 (км²).

Задача 3.

Знайти довжину маятника настінного годинника, якщо кут коливань складає 45°, а довжина дуги, яку описує кінець маятника, дорівнює 30 см.

Розв’язання

Довжина дуги кола визначається за формулою L = ∙.

За умовою L = 30 см, = 45°. Знайдемо радіус – довжину маятника.

R = .

Отже, R = 38(см) – довжина маятника.

Для самостійного розв’язування

Задача 1. Знайдіть площу зрізу ствола дерева, якщо його діаметр дорівнює 0,8 м.

Задача 2. Клумба має форму круга. Довжина кола, що обмежує клумбу, дорівнює 31,4 м. На клумбі висаджують кущі троянд, відводячи під кожний кущ 0,5 м² землі. Яку найбільшу кількість кущів троянд можна висадити на клумбі?

Задача 3. За скільки часу можна облетіти на літаку Землю вздовж екватора на висоті 10 км, рухаючись зі швидкістю 1200 км/год? Результат округліть до 0,1 год. ( Радіус екватора наближено дорівнює 6370 км).

Задача 4. Знайдіть довжину кола, що обмежує круг площею 196см².

Задача 5. Уявіть, що ви обійшли Землю по екватору. На скільки при цьому ваша голова пройшла більше, ніж ноги? Зріст людини дорівнює 1,7 м.

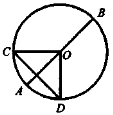
Задачі за малюнком 1. Дано: коло, О — центр кола, АВ — діаметр, CD — хорда, К — середина CD. Довести: АВ CD.
Розв'язання У трикутнику COD: ОС = OD (як радіуси), СК = KD (за умовою). Отже, ∆CОD — рівнобедрений. Тому ОК — медіана, бісектриса і висота трикутника COD. Отже, АВ CD.
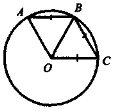
2.Дано: коло, О — центр кола, АВ, ВС — хорди, АВ = ВС = ОС. Знайти: AOC.
Розв'язання ОА = ОВ = ОС (як радіуси). Отже, трикутник АОВ — рівносторонній, тому AOB = 60º. Аналогічно буде рівностороннім трикутник ВОС (ОВ = ВС = CO), тому BOC = 60°. Тоді AOC = AOB + BOC = 60º + 60º = 120º. Відповідь. 120°.
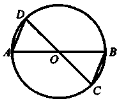
Задачі для самостійного розв’язування Дано: коло, О — центр кола. Довести: AD \|\| ВС, AD = BC.
Дано: коло, О — центр кола, АВ = ВС. Довести: 1 = 2.

Теоретичні відомості:

Означення. Відрізок, який сполучає дві точки кола, називається хордою (рис.1).

Властивості хорд

- Якщо хорди рівновіддалені від центра кола, то вони рівні.

- Якщо хорди рівні, то вони рівновіддалені від центра кола.

- Більша з двох хорд знаходиться ближче до центру кола.

- Хорда, яка проходить через центр є діаметром кола

- Найбільша хорда є діаметром.

- Якщо діаметр ділить хорду навпіл, то він перпендикулярний їй.

- Якщо діаметр перпендикулярний хорді, то він ділить її навпіл.

- При перетині двох хорд добуток відрізків, на які ділиться одна з них точкою перетину, дорівнює добутку відрізків іншої.

Дуги та кути у колі

Означення. Будь-які дві точки A і B на колі розбивають його на дві частини, кожна з цих частин називається дугою (рис.2).

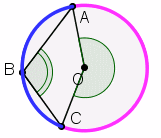
Рис. 2. Дуги та кути у колі
∪AC, ∪ABC - дуги;
<AOC - центральний кут;
<ABC - вписаний кут

Якщо дві сторони кута проходять через ці дві точки, то говорять, що кут спирається на дугу (стягує дугу).

Рівні дуги стягуються рівними хордами.

Дуги, отримані між паралельними хордами, рівні.

Означення. Кут, вершина якого лежить у центрі кола, а сторони перетинають це коло у двох точках, називається центральним кутом (рис.2).

Означення. Кутовою мірою дуги кола називається кутова міра відповідного центрального кута.

Сума кутових мір двох отриманих дуг дорівнює 360^o або 2π радіан. (в залежності від одиниць вимірювання)

Кути як правило вимірюють у градусах або радіанах.

Для заданого кола кутова міра дуги пропорційна її довжині:

Означення. Кут, що утворюється дугою кола, що дорівнює по довжині радіусу кола, приймається за 1 радіан.

Означення. Півколо – це дуга для якої відрізок, що сполучає її кінці, є діаметром

Теореми про кути в колі

Означення. Кут, вершина якого лежить на колі, а сторони перетинають це коло у двох точках, називається вписаним у коло (рис.2).

Теорема. Вписаний у коло кут, сторони якого проходять через дві дані точки кола, дорівнює половині центрального кута, проведеного в ці точки, або доповнює половину центрального кута до 180^o (рис.2).

Ця теорема може бути сформульована по іншому:

Теорема. Вписаний в коло кут дорівнює половині центрального кута, який спирається на та саму дугу в середині кута (рис.2).

Наслідок. Вписані кути, що спираються на одну й ту ж дугу, рівні.

Наслідок. Кути, що спираються на діаметр, дорівнюють 90 °.

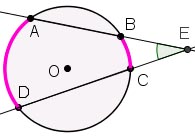
<AED = ½(∪AB-∪CD)
Рис. 5. Кут між січними

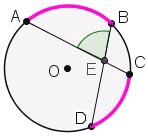
<AEB = ½(∪AB+∪CD)
Рис. 4. Кут між хордами

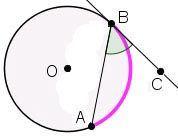
<ABC = ½∪AB
Рис. 3. Кут між хордою і дотичною

Теорема. Кутова міра кута, між хордою і дотичною до кола, проведеної через кінець хорди, дорівнює половині кутової міри дуги, що лежить в даному куті.

Теорема. Кутова міра кута між хордами дорівнює напівсумі кутових мір дуг, що належать даному куту, та відповідному вертикальному куту.

Теорема. Кутова міра кута між січними дорівнює піврізниці дуг, що лежать в даному куті.

Відрізки дотичних до кола, проведених з однієї точки, рівні та утворюють рівні кути з прямою, що проходить через цю точку і центр кола.

Трикутники вписані в коло та описані навколо кола

Теорема. Через три точки, що не лежать на одній прямій, можна провести коло, і притому тільки одне.

Круг та його елементи

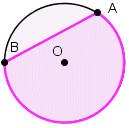
Рис. 6. Круговий сегмент

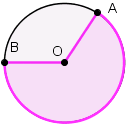
Рис. 5. Круговий сектор

Означення. Геометричне місце точок, віддаль від яких до центра кола не перевищує радіус, називається кругом.

Означення. Область круга, обмежена двома радіусами й дугою називається сектором.

Означення. Область круга, обмежена хордою та дугою, називається сегментом.

Формули пов’язані з колом та кругом

Діаметр кола: d = 2r, де: r - радіус кола.

Довжина кола: l = 2 π r = π d.

Довжина дуги кола: 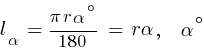$l_alpha~=~{pi r alpha^circ}/{180}~=~r alpha,~~~alpha^circ$ - кут в градусах, - кут в радіанах.

Площа круга 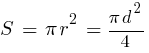$S~=~pi r ^ 2~=~{pi d ^ 2}/{4}$ .

Площа сектора 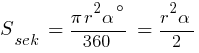$S_sek~=~{pi r ^ 2 alpha^circ}/{360}~=~{r ^ 2 alpha}/{2}$ .

Площа сегмента 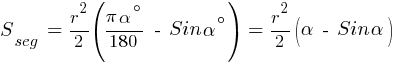$S_seg~=~{r ^ 2}/{2} ({pi alpha^circ}/{180}~-~Sin alpha^circ)~=~{r ^ 2}/{2} (alpha~-~Sin alpha)$ .

Загальне рівняння кола із центром в точці А(x_o;y_o) та радіусом r : (x - x_o)² + (y - y_o)² = r ².

docx

Завантажити

Зберегти на потім

Додав(-ла)

Ясінська Мар'яна Василівна

Пов’язані теми

Геометрія, Розробки уроків

Додано

30 грудня 2021

Переглядів

7661

Оцінка розробки

Відгуки відсутні