Урок "Комбінаторні задачі"

УРОК 37.

Тема уроку: Комбінаторні задачі

Мета уроку:

навчальна: сформувати уявлення про комбінаторику та комбінаторні задачі; розглянути приклади розв'язування найпростіших комбінатор­них задач;

розвивальна: : розвивати логічне мислення, кмітливість;

виховна: виховувати наполегливість.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

I. Організаційний етап.

Перевірити готовність класу до уроку. Налаштування на роботу.

II. Аналіз контрольної роботи .

Виконати швидкий аналіз контрольної роботи. Звернути увагу на типові помилки про її виконанні. Оголосити оцінки за контрольну роботу.

III. Перевірка домашнього завдання.

Поставити запитання до класу по темах вивчених на минулих урокам (можна скористатися конспектом 35 уроку)

IV. Формулювання мети і завдань уроку.

Створити проблемну ситуацію, запропонувавши за­дачу практичного змісту.

У шкільній їдальні на сніданок можна вибрати булку, ватруш­ку, пряник або кекс, а з напоїв — чай, сік або молоко. Скільки різ­них варіантів сніданку можна вибрати?

Після цього повідомити, що ця задача належить до так званих комбінаторних. Вивчає способи розв’язання таких задач розділ математики, який має назву комбінаторика.

Отже, завдання уроку: зрозуміти, що вивчає комбінаторика, ознайомитися з деякими способами розв’язування комбінаторних задач.

V. Сприймання і засвоєння навчального матеріалу.

Комбінаторика — розділ математики, який вивчає комбінації і перестановки предметів, розміщення елементів, що мають певні властивості тощо. Розглянемо задачу.

Задача 1. На пошті у продажу є 5 різних конвертів і 3 різні марки. Скількома способами можна купити конверт з маркою?

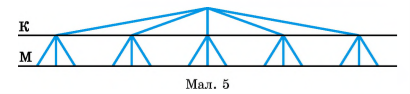
Розв’язання. 1 – й спосіб. Намалюємо дерево можливих варіантів (мал. 5). Позначимо конверт буквою К, марку — буквою М. Малюємо від стовбура 5 гілок (бо є 5 видів конвертів). Оскільки маємо 3 марки, то від кожної з п’яти отриманих точок малюємо по 3 гілки. Рахуємо кількість отриманих унизу точок — 15 і отримуємо відповідь до задачі. Дерево можливих варіантів дає змогу розв’язувати різноманітні задачі, пов’язані з обчисленням кількості способів.

2-й спосіб. Оберемо конверт. У комплект до нього можна вибрати будь- яку з трьох марок. Тому є 3 комплекти,
що містять обраний конверт. Оскільки конвертів усього 5, то кількість різних способів становить 15 (5 3 = 15). Дійшли до важливого правила комбінаторики — правила добутку: якщо елемент кожного такого вибору інший елемент А можна обрати т способами, а після В можна обрати (незалежно від вибору елемента А) п способами, то пару елементів А і В можна обрати т п способами.

Правило добутку можна використовувати, якщо треба обрати більше ніж 2 елементи.

Задача 2. На пошті у продажу є 5 різних конвертів, 3 різні марки і 4 різні вітальні листівки. Скількома способами можна купити комплект, що містить конверт, марку та листівку?

Розв’язання. 5 3 4 = 60 способів.

Розглянемо далі задачу, у якій треба полічити кількість способів, якими можна розмістити в ряд певну  кількість предметів.

Задача 3. Дитина грається трьома іграшками: машинкою, тракторцем, літачком. Скількома способами їх можна викласти в ряд?

Розв’язання. На перше місце можемо поставити одну з трьох іграшок: машинку, тракторець або літачок. Після цього на друге місце можна поставити одну з двох наступних іграшок. Після цього на третє місце ставимо одну іграшку, яка залишилася після вибору перших двох. Використовуючи правило добутку, знайдемо, що іграшки можна розмістити шістьма різними способами (3 2 1). Перевіримо розв’язок задачі за допомогою дерева можливих варіантів (мал. 6).

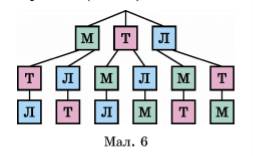
Обчислили кількість способів, якими можна розмістити в ряд кілька предметів. Такі розміщення називають перестановками.
Перестановки позначають буквою Р. У задачі 3 кількість перестановок з трьох елементів дорівнює = 1 2 3; аналогічно кількість перестановок з двох елементів = 1 2; із чотирьох елементів = 1 2 3 4 = 24;
з п’яти Р5 = 1 2 3 4 5 = 120 і т. д.

Розглянемо ще кілька комбінаторних задач.

Задача 4. З даних чисел вибрати такі, які при перестановці цифр утворять числа, у яких число одиниць на 3 більше за число десятків: 42, 36, 74, 14, 85, 92, 47.

Розв’язання. Переставляючи цифри, маємо числа 24, 63, 47, 41, 58, 29, 74. Умову задовольняють числа 74 та 85.

Задача 5. В алфавіті племені БАБА є тільки дві літери «а» і «б». Запиши всі слова цього племені, що містять: 1) дві літери; 2) три літери.

Розв’язання. 1) аа, ба, аб, бб (усього чотири слова); 2) ааа, ааб, аба, абб, ббб, бба, баб, баа (усього вісім слів). Зауважимо, що знайдена кількість слів узгоджується з правилом добутку. Оскільки на кожне місце є два «претенденти» — «а» і «б», то слів, що містять дві літери, має бути 2 2 = 4, а три літери — 2 2 2 = 8.

Розглянемо дві задачі на знаходження конфігурації елементів, що мають певні властивості.

Задача 6. У клітинки квадрата (мал. 7) треба поставити числа 1, 2, 3 та 4 так, щоб числа не повторювалися ані в рядках, ані у стовпчиках, ані по діагоналях (лініях, що ведуть з лівого нижнього кута у правий верхній та з
правого нижнього кута в лівий верхній).

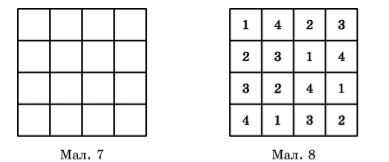
Розв’язання. Один з варіантів розв’язання подано на малюнку 8.

Задача 7. Скількома способами можна розділити 5 цукерок між трьома дітьми так, щоб кожна дитина отримала хоча б по одній цукерці?

Розв’язання. Подамо розв’язок у вигляді таблиці.

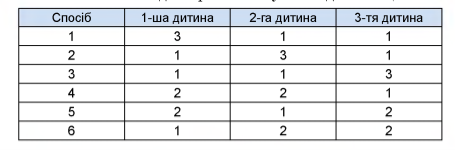
Отже, усього є 6 способів.

VI. Формування вмінь.

Виконання вправ.

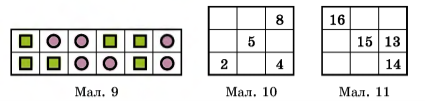
Вправа  487. Які дві фігури (мал. 9) треба переставити місцями, щоб верхній рядок був таким, як нижній?

Вправа 488. Упиши в порожні клітинки (мал. 10) такі числа, щоб квадрат став «магічним», тобто щоб суми чисел у кожному рядку, стовпці та по кожній діагоналі були однакові (спочатку знайди цю суму).

Вправа 490. Костюм складається з блузки та спідниці. Скільки різних костюмів можна скласти з 5 видів блузок і 4 видів спідниць?

Вправа 491. У танцювальному клубі займаються 7 юнаків і 9 дівчат. Скількома способами можна вибрати одну пару для участі в конкурсі?

Вправа 496. Скількома способами можна викласти в ряд червону, білу, чорну та зелену кульки?

Вправа 497. 3 букв розрізної абетки складено слово «учень». Скільки різних послідовностей букв можна отримати, переставляючи букви цього слова?

Вправа 499. Скільки існує двоцифрових чисел, у яких десятків не більше за 4, а одиниць не менше від 8?

Вправа 505. У магазині є книжки, які коштують 10 грн, 20 грн, 50 грн,  70 грн і 80 грн. Учень має 100 грн. Які: 1) дві книжки;
2) три книжки він може купити, витративши всі гроші? Назви всі варіанти.

Вправа 507. Монету підкидають тричі. Скільки різних послідовностей випадання цифри та герба при цьому можна отримати?

Розв’язання. Перший раз може випасти цифра або герб (2 варіанти), другий раз — також 2 варіанти, третій раз – 2 варіанти. Отже, усього послідовностей буде 2 2 2 = = 8.

Вправа 512. У футбольній команді з 11 гравців треба вибрати капітана і його заступника. Скількома способами це можна зробити?

Розв’язання. Капітаном може бути будь-який з 11 гравців. Після вибору капітана на роль його заступника можуть претендувати 10 гравців, що залишилися. Таким чином (за правилом добутку), є 11 10 = 110 різних
варіантів.

Вправа 516. У мішку лежить 6 пар чорних і 6 пар білих рукавичок (усі вони переплутані). Яку найменшу кількість рукавичок потрібно взяти з мішка, не заглядаючи в нього, щоб скомплектувати хоча б одну пару однакових рукавичок?

Вправа 528. Скільки є різних варіантів складання шифру, що містить чотири цифри, якщо цифри: 1) повторюються; 2) не повторюються?

VII. Підсумки уроку.

Запитання до класу:

1. Що вивчає комбінаторика?

2. У чому полягає правило добутку?

3. Що називають перестановками?

4. Як обчислити кількість перестановок з двох, трьох, чотирьох, п’яти предметів?

5. Поясни, як розв’язуються задачі 4— 7.

VIII. Домашнє завдання.

Опрацювати §15 ст. 84 – 92

Вправа 489. Заповни порожні клітинки (мал. 11) так, щоб квадрат став «магічним», попередньо знайшовши суму чисел по діагоналі.