Урок "Квадратична функція, її властивості та графік"

Квадратична функція, її властивості та графік

Урок алгебри в 9 – му класі

Ванда Пашкова, учитель математики спеціалізованої школи I – III ст. № 196, м. Київ

Мета уроку: узагальнити знання учнів про властивості квадратичної функції, відпрацювати навички побудови графіків, їх перетворення;

Розвивати навички самоконтролю, логічне мислення, математичну мову, кмітливість, увагу, уміння працювати самостійно та в групах. Формувати пізнавальний інтерес.

Тип уроку: урок повторення й систематизації  знань.

Обладнання та наочність: конспект, комп’ютерна презентація, картки з тестовими завданнями, інтерактивна дошка, мікрофон.

Хід  уроку

І. Організаційний етап

ІІ. Формування  мети й завдань уроку

Учитель.

Учні класу були заздалегідь об’єднані в три групи, вони самостійно записують кількість набраних балів за кожен вид роботи, підбивають кількість набраних  балів, перетворюють їх в оцінку й оголошують результати наприкінці уроку.

Перш ніж розпочати урок, я хочу звернути вашу увагу на слова, які сказав відомий німецький математик Г.В. Лейбніц:  «Той, хто хоче обмежитися сьогоднішнім без знань минулого, ніколи його не розуміє…». Ці рядки залишаються актуальними й нині, тому що знання – це єдиний цілісний  і нерозривний процес, який має початок, але не має кінця… Бажаю вам не боятися труднощів , впевненості і творчої роботи на уроці. Сьогодні на уроці ми повторимо вивчений матеріал за темою «Квадратична функція, її властивості та графік», розв’яжемо вправи на дослідження квадратичної функції, побудову її графіка. Працюючи на уроці  не забувайте вносити кількість балів на кожному етапі уроку в оцінний лист для самоконтролю.

IІІ. Актуалізація опорних знань

Метод «Мікрофон»

)(Представники кожної команди ставлять по черзі запитання учням інших команд. Якщо учні команди не відповідають на поставлене запитання або дають неправильну відповідь, то запитання адресується учням інших команд).

1. Що називається функцією?
2. Як називається змінна х, змінна у, якщо у =f(х)?
3. Що називається областю визначення функції?
4. Що називається областю значень функції?
5. Що називається нулями функції?
6. Що називають проміжком знакосталості функції?
7. Яка функція називається зростаючою?
8. Яка функція називається спадною?
9. Яка функція називається квадратичною?
10. Яким є графік парної функції?
11. Яким є графік непарної функції?
12. Як, маючи графік функції у =f(х), побудувати графік функції  у = - f(х)?
13. Як, маючи графік функції у =f(х), побудувати графік функції  у = kf(х)?
14. Як, маючи графік функції у =f(х), побудувати графік функції  у = І f(х)І?
15. Як, маючи графік функції у =f(х), побудувати графік функції  у =  f(х) + n?
16. Як, маючи графік функції у =f(х), побудувати графік функції  у =  f(х-n)?
17. Як, маючи графік функції у =f(х), побудувати графік функції  у = f(ІхІ)?
18. Від чого залежить напрям віток параболи?
19. Як знайти координати вершини параболи?
20. Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а < 0?
21. Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а > 0?
22. Які ви знаєте способи побудови параболи?

Учитель. Не забудьте оцінити свої знання в оцінному листі

( 1 бал за правильні  відповіді)

IV. Повторення й систематизація знань, умінь і навичок учнів із вивченої теми

Тест

1.Серед наведених функцій вказати квадратичну.

А) у= 5х + 4;

Б) у =- 3х;

В) у=7 +8;

Г) у=   - 5.

2.Через яку з точок проходить графік функції?

У= 2- 4

А) А(1; 3);   Б) (0; 4); В) (-4; 28); С(-2; 2).

3. На рисунку зображено графік функції У= +bх +с.  Визначити знаки коефіцієнтів a; b;c

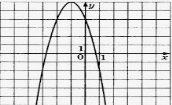
1.а<0, в>0, с<0.  2. а<0, в>0, с>0.     3. а<0, в<0, с<0.    4.  а>0, в>0, с<0.   5.    а>0, в>0, с>0.

6.а<0, в<0, с>0.7.а>0, в<0; с<0. 8. а>0, в<0; с>0.

Відповідь:  6.

4). За даним графіком визначити знаки дискримінанта і коефіцієнта а.

1. а >0;  D>0.  2. а <0;  D>0.  3. а <0;  D>0.   4.а >0;  D<0. 

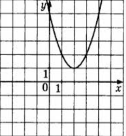
Відповіді:  1.  Б;           2.  В ;              3. 6                4.  4

Учитель.  В оцінний лист записується кількість отриманих балів за тест( максимальна кількість –4 бали)

5).

Відповіді:  1 – Б;  2 – А;  3 – В;   4 – Д.

( максимальна кількість – 2 бали)

6).Робота з підручником

Ст. 114 №4(3);     №11.51.

Оцініть свої знання ( максимальна кількість –2 бали)

Робота в групах

(завдання кожної групи – за 15 хвилин оперативно та правильно виконати завдання. Кожен учень повинен уміти пояснити розв′язання цього завдання. Представник групи пояснює розв′язання  біля дошки, усі інші учні записують умову задачі та її розв′язання в зошит)

1 команда

Задача.

Ділянку землі прямокутної форми обгородили парканом завдовжки 60м. Яку найбільшу площу  матиме ця ділянка?

2 команда

Скільки спільних точок мають графіки функції у = І  - 6ІхІ +8І та у=а залежно від параметра а?

3 команда

Скільки спільних точок мають графіки функції у = -  +4ІхІ -3  та у=а залежно від параметра а?

Оцініть свої знання ( максимальна кількість –3 бали)

Vl. Підбиття підсумків уроку, рефлексія.

Запитання

1. Що було найцікавішим на уроці і чому?
2. Із якими труднощами ви стикалися?
3. Що допомогло подолати труднощі7
4. Чого ви навчилися під час уроку?

Учитель. На уроці ми повторили поняття квадратичної функції, закріпили правила побудови графіка, досліджували властивості  розв′язали вправи з даної теми.

 Ви наполегливо працювали, продемонстрували знання, активність, добре мислили.

( Оцінювання учнів. Підраховується кількість балів, яку кожен учень набрав за урок)

Vll.  Домашнє завдання.

П.11;  №11.49;  ст. 116. № 11;14.